
- •14. Понятие числовой последовательности. Определение. Предел последовательности. Единственность предела числовой последовательности (доказательство).
- •15. Арифметические операции над последовательностями, имеющими пределы (доказательство).
- •16. Понятия бесконечно большой, бесконечно малой и ограниченной последовательностей. Свойства. Теорема о связи бесконечно малой и бесконечно большой последовательностей.
- •4)Теорема:
- •17. Предельный переход в равенствах и неравенствах. Теорема о пределе сжатой последовательности (доказательство).
- •18. Односторонние пределы. Теорема о необходимом и достаточном условии существования предела функции в точке (доказательство).
- •19. Теоремы об арифметических операциях с функциями, имеющими пределы (доказательства).
- •20.Связь понятий предела функции в точке и бесконечно малой функции (доказательство).
- •21. Теорема об обращении непрерывной функции в нуль на замкнутом интервале (Больцано-Коши) (доказательство).
- •22. Односторонние производные функций. Теорема о существовании производной в точке (доказательство).
- •23. Правила вычисления производной суммы, произведения и частного функций (доказательства).
- •24. Вывод формул вычисления производной сложной функции и обратной функции.
- •25. Дифференциал функции. Геометрический смысл дифференциала. Инвариантность формы дифференциала первого порядка.
- •26. Теорема о связи дифференцируемости функции и существовании производной (доказательство).
- •27. Необходимые и достаточные условия возрастания (убывания) функции (доказательство с использованием формулы Лагранжа или двучленной формулы Тейлора).
- •28. Необходимые и достаточные условия локального экстремума непрерывной функции (доказательства для максимума и минимума с использованием трехчленной формулы Тейлора).
- •29. Теоремы о выпуклости (вогнутости) графика непрерывной функции. Точки перегиба. (доказательство с использованием трехчленной формулы Тейлора).
- •30. Определение первообразной функции. Теорема о числе первообразных. Доказательство.
- •31. Вычисление площади области под графиком функции. Вывод формулы Ньютона-Лейбница.
- •32. Вывод формул замены переменной и интегрирования по частям в неопределенном интеграле.
- •36. Теорема о среднем значении определенного интеграла от непрерывной функции. Доказательство.
- •37. Определенный интеграл от непрерывной функции с переменным верхним пределом. Производная. Доказательство. Вывод формулы Ньютона-Лейбница.
- •38. Понятия дифференциального уравнения и его решения. Порядок дифференциального уравнения. Общее, особое, частное решения.
- •39. Задача Коши для уравнения первого порядка. Теорема существования и единственности. (Формулировка).
- •41. Линейные однородные уравнения с постоянными коэффициентами. Характеристическое уравнение. Метод Эйлера. Представление общего решения.
- •42. Линейные неоднородные дифференциальные уравнения. Метод Лагранжа вариации произвольных постоянных.
- •43. Метод неопределенных коэффициентов для построения частных решений неоднородных уравнений с постоянными коэффициентами и правой частью специального вида.
- •44. Подстановка и матричный методы построения общего решения однородной системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами.
- •1. Определение вектора. Операции с векторами. Геометрическая интерпретация. Понятие линейной зависимости и независимости системы векторов.
- •2. Понятие системы координат. Декартова система координат. Примеры. Размерность и базис арифметического пространства. Метрика.
25. Дифференциал функции. Геометрический смысл дифференциала. Инвариантность формы дифференциала первого порядка.
Понятие дифференциала функции
Пусть функция
у=ƒ(х) имеет в точке х отличную от нуля
производную.![]()
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать D у/D х=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.
Таким образом,
приращение функции ∆у представляет
собой сумму двух слагаемых ƒ'(х)•∆х и
а•∆х, являющихся бесконечно малыми
при ∆x→0. При этом первое слагаемое есть
бесконечно малая функция одного порядка
с ∆х, так как![]() а
второе слагаемое есть бесконечно малая
функция более высокого порядка, чем
∆х:
а
второе слагаемое есть бесконечно малая
функция более высокого порядка, чем
∆х:![]()
Поэтому первое слагаемое ƒ'(х)· ∆х называют главной частью приращения функции ∆у.
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х)•∆х.
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (24.1) можно записать так: dy=ƒ'(х)dх, иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Геометрический смысл дифференциала функции
Выясним геометрический смысл дифференциала.
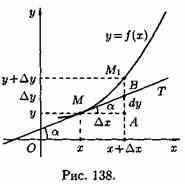
Для этого проведем
к графику функции у=ƒ(х) в точке М(х; у)
касательную МТ и рассмотрим ординату
этой касательной для точки х+∆х (см.
рис. 138). На рисунке ½ АМ½ =∆х, |AM1|=∆у.
Из прямоугольного треугольника МАВ
имеем:![]()
Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.
Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.
 В
этом и состоит геометрический смысл
дифференциала.
В
этом и состоит геометрический смысл
дифференциала.
Рассмотрим функцию y = f(u), где u = f (x), то есть рассмотрим сложную функцию y = f(f(x)). Если каждая из функций f и f являются дифференцируемыми, то производная сложной функции согласно теореме (3) равна y' = f'(u)· u'. Тогда дифференциал функции dy = f'(x)dx = f'(u)u'dx = f'(u)du, du=f(u)du так как u'dx = du. То есть
Последнее равенство означает, что формула дифференциала не изменяется, если вместо функции от x рассматривать функцию от переменной u. Это свойство дифференциала получило название инвариантности формы первого дифференциала.
26. Теорема о связи дифференцируемости функции и существовании производной (доказательство).
Критерий
дифференцируемости: пусть функция f(x)
определена в некотором интервале (а, b)
и
![]() ,
тогда функция f(x) дифференцируема в
точке
,
тогда функция f(x) дифференцируема в
точке
![]() тогда
и только тогда, когда у неё в точке
существует
производная.
тогда
и только тогда, когда у неё в точке
существует
производная.
Доказательство:
![]() пусть
функция f дифференцируема в точке
,
тогда её приращение по определению
представимо в виде:
пусть
функция f дифференцируема в точке
,
тогда её приращение по определению
представимо в виде:
![]()
![]() .
.
![]() ,
то есть производная существует.
,
то есть производная существует.
![]() Пусть
у функции f(x) в точке
существует
производная, то есть существует конечный
предел
Пусть
у функции f(x) в точке
существует
производная, то есть существует конечный
предел
![]() .
.
![]() .
.
![]() .Теорема
доказана.
.Теорема
доказана.
??? Теорема Ферма (об обращении производной в нуль). Графическая интерпретация.
Теорема. Если f(x) – определена на (a,b) и дифференцируема в точке x0 ϵ (a,b), принимает в точке x0 наибольшее или наименьшее значение, то f¢(x0)=0.
Доказательство. Для случая наименьшего значения
f¢(x0+0)=![]() ³
0, f¢(x0-0)=
³
0, f¢(x0-0)=
![]() £
0 Þ f¢(x0)=0
£
0 Þ f¢(x0)=0
Геометрическая интерпретация
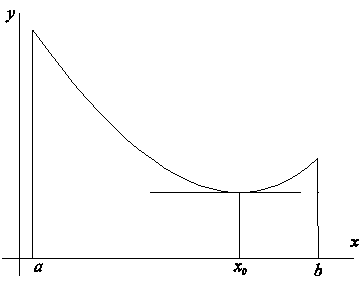
???Теорема Лагранжа (о конечных приращениях). Геометрическая интерпретация.
Формула конечных
приращений или
теорема Лагра́нжа
о среднем значении
утверждает, что если функция
f
непрерывна
на отрезке [a;b]
и дифференцируема
в интервале (a;b),
то найдётся такая точка
![]() ,
что
,
что
![]() .
.
Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Доказательство
Введем функцию
![]() .
Для нее выполнены условия теоремы
Ролля: на концах отрезка ее значения
равны f(a).
Воспользовавшись упомянутой теоремой,
получим, что существует точка c,
в которой производная функции F
равна нулю:
.
Для нее выполнены условия теоремы
Ролля: на концах отрезка ее значения
равны f(a).
Воспользовавшись упомянутой теоремой,
получим, что существует точка c,
в которой производная функции F
равна нулю:
![]()
что и требовалось доказать.
??? Вывод формулы Маклорена для полинома.
Формулой Маклорена называется формула Тейлора при а = 0:
![]()
![]()
Мы получили так называемую формулу Маклорена с остаточным членом в форме Лагранжа.
??? Формула Тейлора для гладкой функции. Представления остаточного члена.
Формула Тейлора
![]()
(Rn(x) - остаточный член формулы Тейлора).
Остаточный член формулы Тейлора
В форме Лагранжа:
![]()
В форме Коши:
![]()
В форме Пеано:
![]() при
при
![]()
В интегральной форме:
![]()
