- •Формула интегрирования по частям для неопределенного интеграла.
- •Основные свойства определенного интеграла Римана: интегрируемость сужения, аддитивное свойство, линейные свойства, интегрируемость произведения.
- •Число e как сумма ряда.
- •Понятие знакочередующегося ряда. Признак Лейбница. Исследование ряда
- •Понятия абсолютно и условно сходящегося числового ряда. Теорема о сходимости абсолютно сходящегося ряда.
- •Основные теоремы о степенных рядах (о непрерывности суммы степенного ряда, о почленном дифференцировании и почленном интегрировании степенного ряда)
- •Разложение функций в степенные ряды (определение).
- •Определения несобственных интегралов 1-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 1-го рода.
- •Определения несобственных интегралов 2-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 2-го рода.
- •Теорема о замене переменной и формула интегрирования по частям для несобственных интегралов.
- •Критерий сходимости несобственного интеграла от неотрицательной функции.
- •Интегральный признак сходимости числового ряда.
- •Скалярное произведение и евклидова норма в (определения). Неравенство Коши-Буняковского.
- •53. Координатные последовательности последовательности точек в . Критерий сходимости последовательности в в терминах координатных последовательностей.
- •58. Понятие функции нескольких переменных
- •Понятие градиента и его арифметические свойства
- •4°. (Здесь предполагается, что g ¹ 0 в соответствующей точке).
- •Определение дифференциалов высших порядков. Иллюстрация определения на примере дифференциалов 1-го и 2-го порядков.
- •79. Формула Тейлора для функции нескольких переменных (включая формулировку теоремы о разложимости функции по формуле Тейлора с остаточным членом в форме Пеано)
- •2) Если же второй дифференциал функции в точке является знакопеременной квадратичной формой, то точка не является точкой локального экстремума функции .
Понятие первообразной функции
Дифференцируемая
на промежутке (а-б) функция Ф’
называется первообразной
функции Ф
на этом промежутке, если
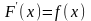
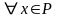 .
.
 -конечный
или бесконечный промежуток.
-конечный
или бесконечный промежуток.
Теорема о двух первообразных функциях
Теорема:
Если Ф1 и Ф2 - две первообразные функции
на промежутке (а,б), то существует такая
постоянная что
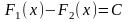 .
.
Д о к а з а т е л ь
с т в о: Так как и – первообразные
функции на промежутке , то
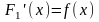 и
и
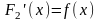 .
Поэтому
.
Поэтому
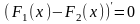 но это, как известно, означает, что
функция
но это, как известно, означает, что
функция
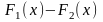 является постоянной на промежутке
является постоянной на промежутке
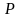 □.
□.
Понятие неопределенного интеграла
Совокупность всех
первообразных функции
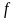 на промежутке
называется неопределенным
интегралом от функции
.
на промежутке
называется неопределенным
интегралом от функции
.
обозначается
следующим образом,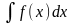 при
этом символ
при
этом символ
 называется
знаком интеграла, а функция
- подынтегральной функцией .
называется
знаком интеграла, а функция
- подынтегральной функцией .
Основные свойства неопределенного интеграла.
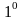 .
Если функция
дифференцируема на промежутке
,
то
.
Если функция
дифференцируема на промежутке
,
то
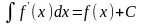 или
или
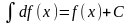 .
. .
Если функция
имеет первообразную , то
.
Если функция
имеет первообразную , то
 следовательно,
следовательно,
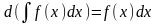 .
.
 .
Если функция
имеет первообразную, то какова бы ни
была постоянная
.
Если функция
имеет первообразную, то какова бы ни
была постоянная
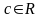 ,
функция
,
функция
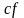 также имеет первообразную, причем всякая
первообразная функции
равна произведению числа
также имеет первообразную, причем всякая
первообразная функции
равна произведению числа
 на некоторую первообразную функции
и, наоборот, всякое такое произведение
есть некоторая первообразная функции
и,
следовательно
на некоторую первообразную функции
и, наоборот, всякое такое произведение
есть некоторая первообразная функции
и,
следовательно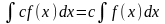 Таким
образом, постоянную можно выносить за
знак неопределенного интеграла.
Таким
образом, постоянную можно выносить за
знак неопределенного интеграла. .
Если функции
.
Если функции
 и
и
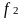 имеют первообразные на промежутке
,то
и функция
имеют первообразные на промежутке
,то
и функция
 имеет на нем первообразную , причем
всякая первообразная функции
является суммой некоторых первообразных
функций
и
;
верно и обратное : всякая такая сумма
является первообразной функции
.Таким образом,
имеет на нем первообразную , причем
всякая первообразная функции
является суммой некоторых первообразных
функций
и
;
верно и обратное : всякая такая сумма
является первообразной функции
.Таким образом,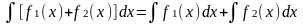 .
.
 .
(Линейность неопределенного интеграла
). Если функции
и
имеют первообразные на промежутке
,
то каковы бы не были вещественные числа
.
(Линейность неопределенного интеграла
). Если функции
и
имеют первообразные на промежутке
,
то каковы бы не были вещественные числа
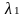 и
и
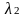 ,
функция
,
функция
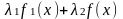 также имеет первообразную на промежутке
, причем
.
также имеет первообразную на промежутке
, причем
.
Формула интегрирования по частям для неопределенного интеграла.
Теорема: Пусть
функции
 и
и
 дифференцируемы на промежутке
и существует первообразная функции
дифференцируемы на промежутке
и существует первообразная функции
 . Тогда существует и первообразная
функции
. Тогда существует и первообразная
функции
 ,а
также имеет место формула
,а
также имеет место формула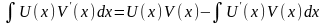 (формула
интегрирования по частям).
(формула
интегрирования по частям).
Д о к а з а т е л ь
с т в о. По правилу дифференцирования
произведения дифференцируемых функций
имеет место формула
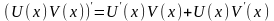 .
Запишем в виде
.
Запишем в виде
 .
По условию
функция
.
По условию
функция
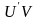 имеет первообразную; функция
имеет первообразную; функция
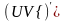 также имеет первообразную (ей является
функция
также имеет первообразную (ей является
функция
 ).
Поэтому в силу свойства линейности
неопределенного интеграла из предыдущего
равенства следует, что первообразную
имеет и функция
,
причем
).
Поэтому в силу свойства линейности
неопределенного интеграла из предыдущего
равенства следует, что первообразную
имеет и функция
,
причем

Формула замены переменной в неопределенном интеграле
Теорема: Пусть
функция
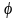 имеет первообразную
имеет первообразную
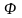 на промежутке
,
а функция
дифференцируема на промежутке
на промежутке
,
а функция
дифференцируема на промежутке
 и
и
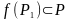 .
Тогда
.
Тогда

Док-во: по условию
-
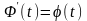 .
Поэтому по правилу дифференцирования
сложной функции имеем
.
Поэтому по правилу дифференцирования
сложной функции имеем
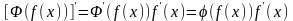 а это
означает, что
а это
означает, что
 -
первообразная функции
-
первообразная функции и, следовательно, по определению
неопределенного интеграла имеет место
равенство□.
и, следовательно, по определению
неопределенного интеграла имеет место
равенство□.
Понятие интегральной суммы Римана и ее геометрический смысл.
Любой конечный,
упорядоченный набор точек
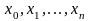 ,
такой, что
,
такой, что
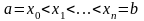 ,
,
называется
разбиением
отрезка
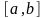 (при
том, что функция
определена на отрезке
).
(при
том, что функция
определена на отрезке
).
Разбиение
отрезка
будем обозначать далее буквой
 ,
при этом будем писать
,
при этом будем писать

Пусть задано
некоторое разбиение отрезка
.
Всякий отрезок
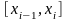 ,
,
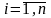 будем называть частичным
отрезком разбиения
.
будем называть частичным
отрезком разбиения
.
Положим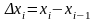 ,
,
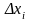 - длина
частичного
отрезка
разбиения
.
- длина
частичного
отрезка
разбиения
.
Выберем в каждом
из частичных отрезков разбиения
произвольно по точке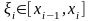 ,
и
составим сумму
,
и
составим сумму
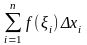 . Эта сумма называется интегральной
суммой
функции
на отрезке
,
соответствующей разбиению
и системе точек
. Эта сумма называется интегральной
суммой
функции
на отрезке
,
соответствующей разбиению
и системе точек
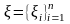 ,
,
.
Поэтому далее она иногда будет обозначаться
символом
,
,
.
Поэтому далее она иногда будет обозначаться
символом
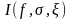 .
Таким образом,
.
Таким образом,
 .
.
Геометрический смысл
Понятия об интегрируемой по Риману функции и ее определенном интеграле.
Ранг разбиения
:Число назовем
рангом или диаметром разбиения
.
назовем
рангом или диаметром разбиения
.
Интегральная сумма: .
Число
 называется пределом
интегральных сумм функции
называется пределом
интегральных сумм функции
 на отрезке
при
на отрезке
при
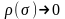 ,
если
,
если
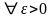
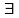
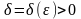 такое, что для любого разбиения
отрезка
с
такое, что для любого разбиения
отрезка
с
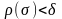 независимо от выбора системы точек
,
,
,
имеет место неравенство
независимо от выбора системы точек
,
,
,
имеет место неравенство
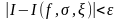
Если существует предел интегральных сумм функции на отрезке при , то функция называется интегрируемой по Риману на этом отрезке, а сам этот предел называется определенным интегралом Римана функции на отрезке .
Необходимое условие интегрируемости функции по Риману
Теорема 1. Если функция интегрируема по Риману на отрезке , то она ограничена на этом отрезке.
Д о к а з а т е л ь
с т в о. Предположим противное. Пусть
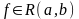 ,
но
неограничена на отрезке
.Выберем
,
но
неограничена на отрезке
.Выберем
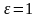 .
Так как
,
то
.
Так как
,
то
 такое, что для любого разбиения
отрезка
с
и для любой системы точек
,
взятых по одной из каждого частичного
отрезка разбиения
имеет место неравенство
такое, что для любого разбиения
отрезка
с
и для любой системы точек
,
взятых по одной из каждого частичного
отрезка разбиения
имеет место неравенство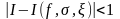 ,где
,где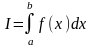 Поэтому
для любого разбиения
с
и для любой указанной выше системы
точек
Поэтому
для любого разбиения
с
и для любой указанной выше системы
точек
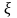
 Таким
образом множество
Таким
образом множество
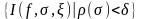 |
является ограниченным. Выберем одно из
разбиений
с
.
Так как по предположению функция
неограничена на отрезке
,
то она неограничена хотя бы на одном
частичном отрезке
|
является ограниченным. Выберем одно из
разбиений
с
.
Так как по предположению функция
неограничена на отрезке
,
то она неограничена хотя бы на одном
частичном отрезке
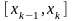 этого разбиения. Для определенности
будем считать, что она неограничена на
нем сверху (случай ее неограниченности
снизу рассматривается аналогично).
Тогда за счет выбора точки
этого разбиения. Для определенности
будем считать, что она неограничена на
нем сверху (случай ее неограниченности
снизу рассматривается аналогично).
Тогда за счет выбора точки
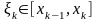 слагаемое
слагаемое
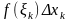 в интегральной сумме (2), а вместе с ним
и вся эта интегральная сумма может быть
сделана сколь угодно большой. Последнее
противоречит ограниченности описанного
выше множества интегральных сумм функции
.
Полученное противоречие доказывает
теорему
в интегральной сумме (2), а вместе с ним
и вся эта интегральная сумма может быть
сделана сколь угодно большой. Последнее
противоречит ограниченности описанного
выше множества интегральных сумм функции
.
Полученное противоречие доказывает
теорему
Понятия верхней и нижней суммы Дарбу функции, их связь с интегральной суммой Римана и геометрический смысл сумм Дарбу.
Пусть функция ограничена на отрезке и - некоторое разбиение этого отрезка.
Положим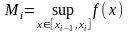 ,
,
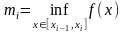 Верхняя
сумма -
Верхняя
сумма -
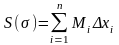 ,
нижняя
-
,
нижняя
-
 ,
где
,
.
Независимо от выбора системы точек
,
где
,
.
Независимо от выбора системы точек
 ,
,
,
имеют место неравенства
,
,
,
имеют место неравенства
 ,то
есть всякая интегральная сумма функции
на отрезке
,
соответствующая выбранному разбиению
,
лежит между нижней и верхней своими
суммами Дарбу, соответствующими тому
же разбиению
.
,то
есть всякая интегральная сумма функции
на отрезке
,
соответствующая выбранному разбиению
,
лежит между нижней и верхней своими
суммами Дарбу, соответствующими тому
же разбиению
.
Геометрический смысл?
Свойства сумм Дарбу (предварительно сформулировать определение измельчения разбиения)
Разбиение
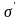 отрезка
называется измельчением
разбиения
того же отрезка, если каждая точка
разбиения
является также и точкой разбиения
,
то есть если
отрезка
называется измельчением
разбиения
того же отрезка, если каждая точка
разбиения
является также и точкой разбиения
,
то есть если
 .
.
Свойство 10.
Пусть
-измельчение
разбиения
.
Тогда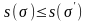 ,а
,а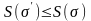 ,то
есть при измельчении разбиения нижние
суммы Дарбу не убывают, а верхние суммы
Дарбу не возрастают. Свойство 20.
Любая нижняя сумма Дарбу не превосходит
любой верхней суммы Дарбу, то есть для
любых двух разбиений
,то
есть при измельчении разбиения нижние
суммы Дарбу не убывают, а верхние суммы
Дарбу не возрастают. Свойство 20.
Любая нижняя сумма Дарбу не превосходит
любой верхней суммы Дарбу, то есть для
любых двух разбиений
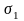 и
и
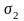 отрезка
имеет место неравенство
отрезка
имеет место неравенство
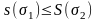
Понятие верхнего и нижнего интегралов Дарбу
Пусть, как и выше,
функция
ограничена на отрезке
.По
третьему свойству сумм Дарбу нижние
суммы Дарбу ограничены сверху, а верхние
суммы Дарбу ограничены снизу. Поэтому
числа и
и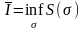 являются
конечными (здесь точные грани берутся
по всевозможным разбиениям отрезка
).
В силу того же третьего свойства сумм
Дарбу для любых разбиений
являются
конечными (здесь точные грани берутся
по всевозможным разбиениям отрезка
).
В силу того же третьего свойства сумм
Дарбу для любых разбиений
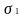 и
и
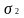 отрезка
отрезка
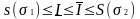 и, в частности,
для любого разбиения
отрезка
и, в частности,
для любого разбиения
отрезка
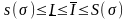 .
Числа
.
Числа
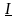 и
и
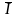 называются, соответственно, нижним и
верхним интегралами Дарбу функции
на отрезке
.
называются, соответственно, нижним и
верхним интегралами Дарбу функции
на отрезке
.
Критерий интегрируемости функции по Риману и его следствие
Для того, чтобы
ограниченная на отрезке
функция
была интегрируемой по Риману на этом
отрезке необходимо и достаточно, чтобы
для любого
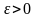 нашлось такое разбиение
отрезка
,
что
нашлось такое разбиение
отрезка
,
что
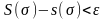 Следствие.
Для того, чтобы ограниченная на отрезке
Следствие.
Для того, чтобы ограниченная на отрезке
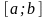 функция
была интегрируемой по Риману на этом
отрезке, необходимо и достаточно, чтобы
ее верхний и нижний интегралы Дарбу
совпадали друг с другом:
функция
была интегрируемой по Риману на этом
отрезке, необходимо и достаточно, чтобы
ее верхний и нижний интегралы Дарбу
совпадали друг с другом:
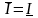 ,т.е.
,т.е.
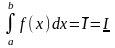 .
.
Понятие площади плоской фигуры и геометрический смысл определенного интеграла Римана
Площадь плоской
фигуры – множество точек на плоскости
А, если существует такой прямоугольник
Р, что О соответствует Р.no1.
Понятие площади Определение
1. Множество
точек на плоскости называется элементарным,
если оно представляет собой объединение
конечного числа прямоугольников со
сторонами, параллельными осям координат.Без
ущерба для общности в этом определении
можно считать, что соответствующие
прямоугольники пересекаются разве лишь
по своим сторонам. Хотя одно и то же
элементарное множество разными способами
можно представить в виде объединения
конечного числа прямоугольников,
пересекающихся разве лишь по своим
сторонам, сумма площадей этих прямоуголников
будет одной и той же и эту сумму естественно
назвать площадью элементарного множества.
Таким образом, если
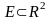 – элементарное множество и
– элементарное множество и
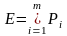 ,
где
,
где
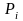 (
( )
– прямоугольники, которые пересекаются
разве лишь по своим сторонам, то площадь
)
– прямоугольники, которые пересекаются
разве лишь по своим сторонам, то площадь
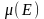 элементарного множества
элементарного множества
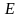 находится по формуле
находится по формуле
 .Определение
2. Множество
точек на плоскости
.Определение
2. Множество
точек на плоскости
 называется ограниченным или также –
плоской фигурой, если существует такой
прямоугольник
,
что
называется ограниченным или также –
плоской фигурой, если существует такой
прямоугольник
,
что
 .
.
Определение 3. Внешней мерой Жордана плоской фигуры называется число
|
(здесь точная нижняя грань берется по всем элементарным множествам, содержащим в себе множество ).
Определение 4. Внутренней мерой Жордана плоской фигуры называется число
|
(2) |
(здесь точная верхняя грань берется по всем элементарным множествам, содержащимся во множестве ).
Определение
5. Пусть
– ограниченное множество точек на
плоскости (т.е. плоская фигура). Множество
– называется измеримым по Жордану, если
 ,при
этом число
,при
этом число
 называется мерой Жордана множества
или площадью этого множества.
называется мерой Жордана множества
или площадью этого множества.