Основные свойства определенного интеграла Римана: интегрируемость сужения, аддитивное свойство, линейные свойства, интегрируемость произведения.

п^о1. Интегрируемость сужения. Пусть функция определена на отрезке . Если функция интегрируема на отрезке , то она интегрируема и на любом отрезке .

n^о2. Аддитивное свойство интеграла. Если функция интегрируема на каждом из отрезков и ( ), то она интегрируема и на отрезке , причем

п^о3. Линейные свойства интеграла Римана. Пусть функции и интегрируемы на отрезке . Тогда их сумма также интегрируема на этом отрезке, причем

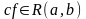
Если , то , причем

п^о4. Интегрируемость произведения интегрируемых по Риману функций.Если , то

Неравенства для интегралов и интегрируемость модуля интегрируемой по Риману функции.

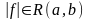Пусть и на . Тогда . Если , то , причем

Определенный интеграл, как функция верхнего предела интегрирования, формула Ньютона-Лейбница.

Если функция непрерывна на отрезке , то какова бы ни была ее первообразная на этом отрезке, справедлива формула (2) формула Ньютона-Лейбница

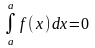Д о к а з а т е л ь с т в о. Пусть – некоторая первообразная функции на отрезке . Так как по первому следствию из теоремы 1 функция ,также является ее первообразной на этом отрезке, то (3) Полагая здесь , с учетом равенства будем иметь 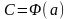. Поэтому равенство (3) можно записать так: .Формула (2) получается отсюда при

Классы интегрируемых по Риману функций.

n1. Интегрируемость непрерывных и монотонных функций . Теорема1Непрерывная на отрезке функция интегрируема по Риману на этом отрезке.

Теорема2. Всякая монотонная на отрезке функция интегрируема по Риману на этом отрезке.

n˚2. Классы разрывных функций, интегрируемых по Риману. Теорема1. Всякая ограниченная на отрезке функция , которая имеет на нем конечное число точек разрыва, интегрируема по Риману на этом отрезке. Теорема 2 (Лебег). Для того, чтобы ограниченная на отрезке функция была интегрируема по Риману на этом отрезке необходимо и достаточно, чтобы множество ее точек разрыва на этом отрезке имело лебегову меру нуль.

Формула замены переменной в определенном интеграле

Определение 1. Если функция имеет на промежутке непрерывную производную , то она называется непрерывно дифференцируемой на этом промежутке. Теорема 1. Пусть функция непрерывна на промежутке , а функция непрерывно дифференцируема на отрезке и , причем , а . Тогда

Формула интегрирования по частям для определенного интеграла.

Если функци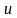и и 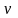непрерывно дифференцируемы на отрезке с концами в точках и 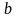, то справедлива следующая формула

Понятие числового ряда. Частичные суммы ряда. Сходящиеся и расходящиеся ряды, сумма ряда.

Пусть - последовательность вещественных чисел. Формальная сумма всех членов этой последовательности обозначаемая, обычно, символом называется числовым рядом.

Пусть дан ряд. Сумма первых n его членов: называется (n-ой) частичной суммой ряда.

Числовой ряд называется сходящимся, если сходится последовательность его частичных сумм, при этом предел этой последовательности

называется суммой ряда. Если последовательность частных сумм рядарасходится, то его, соответственно, называют расходящимся.

Суммой рядов 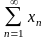и называется ряд

Ряд бесконечной геометрической прогрессии.

Рассмотрим ряд члены которого составляют бесконечную геометрическую прогрессию со знаменателем q. Этот ряд будем называть далее рядом бесконечной геометрической прогрессии.

Критерий Коши сходимости числового ряда и необходимое условие его сходимости.

Теорема 2 (Критерий Коши). Для сходимости числового ряда необходимо и достаточно, чтобы 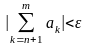или, равносильно, чтобы

Следствие. (Необходимое условие сходимости ряда). Если ряд (1) сходится, то его общий член стремится к нулю: .

Исследование гармонического ряда.

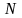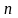условие сходимости ряда Коши не является достаточным. Рассмотрим так называемый гармонический ряд. Очевидно для него . Покажем, тем не менее, что ряд расходится. Для этого в силу критерия Коши достаточно показать что : . Выберем и произвольное . В качестве выберем любое натуральное число, большее чем , а в качестве то же число , т.е. . Тогда будем иметь Следовательно – искомое и по критерию Коши гармонический ряд расходиться.

Критерий сходимости ряда с неотрицательными членами и теорема (признак) сравнения для числовых рядов.

Ряд (1) все члены которого – неотрицательные числа, называется рядом с неотрицательным членами.

Теорема 1 (Критерий сходимости ряда с неотрицательными членами). Числовой ряд с неотрицательными членами сходиться тогда и только тогда, когда последовательность его частичных сумм ограничена сверху.Теорема 2 (теорема сравнения). Пусть ряды (2)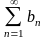 (3) имеют неотрицательные члены ( и ) и (4). Тогда 1)если ряд (3) сходится, то сходится и ряд (2); 2) если ряд (2) расходится, то расходится и ряд (3).

Д о к а з а т е л ь с т в о. Пусть ряд (3) сходиться. Тогда по теореме 1 последовательность его частичных сумм

ограниченна сверху : 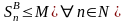, а так как в силу неравенства (4) ,то т.е. ограничена сверху и последовательность частичных сумм ряда (2). Тогда, опять-таки по теореме 1 этот ряд также сходится. Утверждение i) вытекает из ii), если рассуждать от противного. Действительно, пусть ряд (2) расходится, но вопреки утверждению ряд (3) сходится. Тогда по утверждению i) сходится и ряд (2), что противоречит условию □ n^o2. Следствия из теоремы сравнения. Следствие 1. Пусть каждый из рядов (1) . (2) имеет положительные члены и существует предел (3). Тогда при из сходимости ряда (2) вытекает сходимость и ряда (1), а при 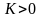из расходимости ряда (2) вытекает расходимость и ряда (1). Таким образом, при оба ряда (1) и (2) сходятся или нет одновременно. Следствие 2. Пусть каждый из рядов (1) и (2) имеет положительные члены и существует такое, что (4). Тогда из сходимости ряда (2) вытекает и сходимость ряда (1), а из расходимости ряда (1) вытекает и расходимость ряда (2).

Признаки сходимости числовых рядов Коши и Д^'аламбера Теорема 4 (признак Коши). Пусть ряд (1) имеет неотрицательные члены и существует предел (2). Тогда если , то ряд (1) сходится; если , то ряд (1) расходится; существуют как сходящиеся, так и расходящиеся ряды, для которых .Теорема 5 (Признак Д’аламбера). Пусть ряд (1) имеет положительные члены и существует предел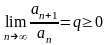 . (3)Тогда1) если , то ряд (1) сходится;2) если , то ряд (1) расходится;3) существуют как сходящиеся, так и расходящиеся ряды, для которых .признаку Д’аламбера он сходится.Пусть 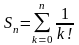, .Поскольку ≜ , то с учетом определения суммы ряда для доказательства равенства (5) достаточно доказать, что = (6) По формуле бинома Ньютона (при ) имеем .

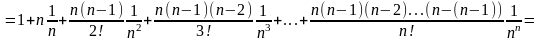
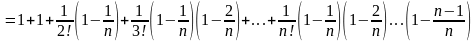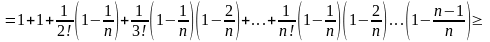
Следовательно . Переходя в этом неравенстве к пределу при будем иметь . (7) Заметим теперь, что если , то .Фиксируя здесь и переходя к пределу при , получим Теперь переходя в этом неравенстве к пределу при , будем иметь . (8) Из (7) и (8) следует (6) □

Теорема Коши о рядах с неотрицательными членами и исследование обобщенного гармонического ряда – ряда . Теорема 3. Если (1) то ряд (2) сходится тогда и только тогда, когда сходится ряд (3) Предложение 1. Ряд (4) сходится, если и расходится, если .Д о к а з а т е л ь с т в о. Если , то общий член ряда (4) не стремится к нулю, т.е. не выполнено необходимое условие сходимости ряда. Следовательно, при этих ряд (4) расходится. Пусть . Тогда члены ряда (4) удовлетворяют всем условиях теоремы Коши и, следовательно, по этой теореме он сходится тогда и только тогда, когда сходится ряд ,где . Последний ряд – ряд бесконечной геометрической прогрессии,– как известно, сходится только в случае, когда , т.е. когда 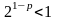, а это имеет место, лишь если □

Предложение 2. Если , то ряд (5)сходится. Если же , то он расходится.Д о к а з а т е л ь с т в о. Если , то .

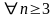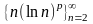Следовательно при . Так как гармонический ряд расходится, то по теореме сравнения отсюда следует, что при расходится и ряд (5). Пусть . Поскольку степенная функция (при ) и функция – возрастающие, возрастающей является и последовательность . Поэтому последовательность убывает и можно применить теорему Коши, согласно которой ряд (5) сходится тогда и только тогда, когда сходится ряд . В силу предложения 1 этот ряд сходится при и расходится при □