
- •Формула интегрирования по частям для неопределенного интеграла.
- •Основные свойства определенного интеграла Римана: интегрируемость сужения, аддитивное свойство, линейные свойства, интегрируемость произведения.
- •Число e как сумма ряда.
- •Понятие знакочередующегося ряда. Признак Лейбница. Исследование ряда
- •Понятия абсолютно и условно сходящегося числового ряда. Теорема о сходимости абсолютно сходящегося ряда.
- •Основные теоремы о степенных рядах (о непрерывности суммы степенного ряда, о почленном дифференцировании и почленном интегрировании степенного ряда)
- •Разложение функций в степенные ряды (определение).
- •Определения несобственных интегралов 1-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 1-го рода.
- •Определения несобственных интегралов 2-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 2-го рода.
- •Теорема о замене переменной и формула интегрирования по частям для несобственных интегралов.
- •Критерий сходимости несобственного интеграла от неотрицательной функции.
- •Интегральный признак сходимости числового ряда.
- •Скалярное произведение и евклидова норма в (определения). Неравенство Коши-Буняковского.
- •53. Координатные последовательности последовательности точек в . Критерий сходимости последовательности в в терминах координатных последовательностей.
- •58. Понятие функции нескольких переменных
- •Понятие градиента и его арифметические свойства
- •4°. (Здесь предполагается, что g ¹ 0 в соответствующей точке).
- •Определение дифференциалов высших порядков. Иллюстрация определения на примере дифференциалов 1-го и 2-го порядков.
- •79. Формула Тейлора для функции нескольких переменных (включая формулировку теоремы о разложимости функции по формуле Тейлора с остаточным членом в форме Пеано)
- •2) Если же второй дифференциал функции в точке является знакопеременной квадратичной формой, то точка не является точкой локального экстремума функции .
Основные теоремы о степенных рядах (о непрерывности суммы степенного ряда, о почленном дифференцировании и почленном интегрировании степенного ряда)
Пусть
–
радиус сходимости степенного ряда
 (1).Теорема 1
(о непрерывности суммы степенного ряда).
Сумма степенного ряда является непрерывной
функцией на интервале сходимости
этого ряд. .Говорят, что функциональный
ряд
можно
интегрировать почленно на отрезке
(1).Теорема 1
(о непрерывности суммы степенного ряда).
Сумма степенного ряда является непрерывной
функцией на интервале сходимости
этого ряд. .Говорят, что функциональный
ряд
можно
интегрировать почленно на отрезке
 ,
если
,
если
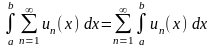 .Теорема
2 (о почленном интегрировании степенного
ряда).
Степенной ряд (1) можно почленно
интегрировать на любом отрезке
.Теорема
2 (о почленном интегрировании степенного
ряда).
Степенной ряд (1) можно почленно
интегрировать на любом отрезке
 ,
где
,
где
 ,
при этом степенной ряд
,
при этом степенной ряд
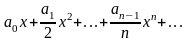 (2)
полученный в результате почленного
интегрирования ряда (1) имеет тот же
радиус сходимости, что и исходный ряд
(1).Теорема 3
(о почленном
дифференцировании степенного ряда).
Степенной
ряд (1) можно почленно дифференцировать
в любой точке
из интервала его сходимости
,
при этом степенной ряд
(2)
полученный в результате почленного
интегрирования ряда (1) имеет тот же
радиус сходимости, что и исходный ряд
(1).Теорема 3
(о почленном
дифференцировании степенного ряда).
Степенной
ряд (1) можно почленно дифференцировать
в любой точке
из интервала его сходимости
,
при этом степенной ряд
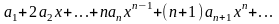 (3)
полученный почленным дифференцированием
ряда (1) имеет тот же радиус сходимости,
что и исходный ряд (1).
(3)
полученный почленным дифференцированием
ряда (1) имеет тот же радиус сходимости,
что и исходный ряд (1).
Разложение функций в степенные ряды (определение).
Пусть функция
определена на некотором числовом
множестве
.Определение
1. Говорят,
что функция
разлагается в окрестности
точки
в степенной ряд
 ,
если
,
если
 ,
.(1)
,
.(1)
Необходимое условие разложимости функции в степенной ряд. Единственность разложения. Понятия ряда Тейлора и ряда Маклорена.
Теорема 1
(необходимое условие разложимости
функции в степенной ряд).
Для того,
чтобы функция
могла быть разложена в окрестности
точки
в степенной ряд
,
необходимо, чтобы она имела в ней
производные любого порядка.Д
о к а з а т е л ь с т в о.
Действительно, если в окрестности точки
имеет место равенство (1), то эта окрестность
заведомо содержится в интервале
сходимости степенного ряда, стоящего
в правой части равенства (1). А поскольку
степенной ряд можно любое число раз
почленно дифференцировать в его интервале
сходимости, то это и означает, что функция
в окрестности точки
имеет производные любого порядка
□Теорема 2.
Если функция
разлагается в окрестности точки
в степенной ряд
,
то лишь единственным образом. Определение
2. Степенной
ряд
,
коэффициенты которого определяются по
формуле
 называется
рядом Тейлора функции
в точке
. Ряд
Тейлора функции
в точке
называется
рядом Тейлора функции
в точке
. Ряд
Тейлора функции
в точке
 ,
т.е. ряд
,
т.е. ряд
 называется ее рядом Маклорена.
называется ее рядом Маклорена.
Разложение
элементарных функций в ряд тейлора.
Вспомним
теперь, что для
раз дифференцируемой в точке
функции
ее формула Тейлора в этой точке или, что
то же самое, ее формула Маклорена имеет
вид ,где
,где
 –
-ый
остаток формулы Маклорена. Тогда
учитывая, что разложимость на интервале
бесконечно дифференцируемой на нем
функции
в свой ряд Тейлора (в точке
)
означает, что
–
-ый
остаток формулы Маклорена. Тогда
учитывая, что разложимость на интервале
бесконечно дифференцируемой на нем
функции
в свой ряд Тейлора (в точке
)
означает, что ри
ри
 ,
приходим к следующему, очевидному
заключению: Теорема
3. Для того,
чтобы бесконечно дифференцируемая в
точке
функция
разлагалась на интервале
в свой ряд Маклорена, необходимо и
достаточно, чтобы остаточный член в
формуле Маклорена для этой функции
стремился к нулю на этом интервале:
,
приходим к следующему, очевидному
заключению: Теорема
3. Для того,
чтобы бесконечно дифференцируемая в
точке
функция
разлагалась на интервале
в свой ряд Маклорена, необходимо и
достаточно, чтобы остаточный член в
формуле Маклорена для этой функции
стремился к нулю на этом интервале:
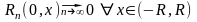 .Пользуясь
этой теоремой и тем, что для бесконечно
дифференцируемых на всей числовой
прямой функций
.Пользуясь
этой теоремой и тем, что для бесконечно
дифференцируемых на всей числовой
прямой функций
 их формулы Маклорена с остаточными
членами в форме Лагранжа имеют вид:
их формулы Маклорена с остаточными
членами в форме Лагранжа имеют вид:


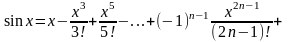


 (здесь
всюду точка
лежит строго между точками 0 и
),
легко приходим к выводу, что все эти
три функции разлагаются в свой ряд
Маклорена на всей вещественной прямой
и эти разложения имеют соответственно
вид:
(здесь
всюду точка
лежит строго между точками 0 и
),
легко приходим к выводу, что все эти
три функции разлагаются в свой ряд
Маклорена на всей вещественной прямой
и эти разложения имеют соответственно
вид:

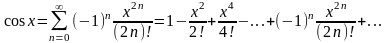 Рассмотрим
функцию
Рассмотрим
функцию
 .
По формуле Маклорена (2) для
.
По формуле Маклорена (2) для
 имеем
имеем .Запишем здесь остаточный член в форме
Лагранжа:
.Запишем здесь остаточный член в форме
Лагранжа: .Тогда
если
.Тогда
если
 ,
то
,
то
 .
Поэтому
.
Поэтому
 и, следовательно,
и, следовательно, при
при
 .
Если же
.
Если же
 ,
то запишем остаточный член в форме
Коши:
,
то запишем остаточный член в форме
Коши: ,Так
как при
,Так
как при
 и
и ,то
при тех же
имеем
,то
при тех же
имеем и,
следовательно,
при
Из (3) и (4), с учетом формулы Маклорена
для функции
и,
следовательно,
при
Из (3) и (4), с учетом формулы Маклорена
для функции
 ,
следует что она раскладывается в свой
ряд Маклорена на промежутке
,
следует что она раскладывается в свой
ряд Маклорена на промежутке
 .
и это разложение имеет вид:
.
и это разложение имеет вид:  Заметим,
что радиус сходимости ряда, стоящего
здесь справа равен 1, а в точке
Заметим,
что радиус сходимости ряда, стоящего
здесь справа равен 1, а в точке
 он заведомо расходится. Так-что, последнее
разложение имеет место только на
промежутке
.
Приведем еще
разложение функции
он заведомо расходится. Так-что, последнее
разложение имеет место только на
промежутке
.
Приведем еще
разложение функции
 .
Дифференцируя эту функцию и используя
формулу для суммы бесконечной
геометрической прогрессии будем иметь
.
Дифференцируя эту функцию и используя
формулу для суммы бесконечной
геометрической прогрессии будем иметь ,
,
 .Ряд,
стоящий здесь справа имеет радиус
сходимости
.Ряд,
стоящий здесь справа имеет радиус
сходимости
 .
Поэтому его можно интегрировать почленно
на любом отрезке
,
где
.
Поэтому его можно интегрировать почленно
на любом отрезке
,
где
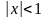 .
Интегрируя правую и левую часть равенства
(5) по любому такому отрезку будем иметь
.
Интегрируя правую и левую часть равенства
(5) по любому такому отрезку будем иметь
 Однако
можно показать, что ряд, стоящий в правой
части равенства (6) сходится и в точках
Однако
можно показать, что ряд, стоящий в правой
части равенства (6) сходится и в точках
 ,
в чем легко убеждаемся по признаку
Лейбница. Более того, можно показать
(см., например, учебник Кудрявцева), что
разложение (5) справедливо и в точках
.
Таким образом справедливо разложение
,
в чем легко убеждаемся по признаку
Лейбница. Более того, можно показать
(см., например, учебник Кудрявцева), что
разложение (5) справедливо и в точках
.
Таким образом справедливо разложение Наконец,
без доказательства отметим, что функция
Наконец,
без доказательства отметим, что функция
 на интервале
на интервале
 имеет следующее разложение
имеет следующее разложение .При
в зависимости
от значения показателя степени
.При
в зависимости
от значения показателя степени
 это разложение может иметь место, а
может и нет ! См. по этому поводу учебники
Кудрявцева и Фихтенгольца.
это разложение может иметь место, а
может и нет ! См. по этому поводу учебники
Кудрявцева и Фихтенгольца.
