
- •Формула интегрирования по частям для неопределенного интеграла.
- •Основные свойства определенного интеграла Римана: интегрируемость сужения, аддитивное свойство, линейные свойства, интегрируемость произведения.
- •Число e как сумма ряда.
- •Понятие знакочередующегося ряда. Признак Лейбница. Исследование ряда
- •Понятия абсолютно и условно сходящегося числового ряда. Теорема о сходимости абсолютно сходящегося ряда.
- •Основные теоремы о степенных рядах (о непрерывности суммы степенного ряда, о почленном дифференцировании и почленном интегрировании степенного ряда)
- •Разложение функций в степенные ряды (определение).
- •Определения несобственных интегралов 1-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 1-го рода.
- •Определения несобственных интегралов 2-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 2-го рода.
- •Теорема о замене переменной и формула интегрирования по частям для несобственных интегралов.
- •Критерий сходимости несобственного интеграла от неотрицательной функции.
- •Интегральный признак сходимости числового ряда.
- •Скалярное произведение и евклидова норма в (определения). Неравенство Коши-Буняковского.
- •53. Координатные последовательности последовательности точек в . Критерий сходимости последовательности в в терминах координатных последовательностей.
- •58. Понятие функции нескольких переменных
- •Понятие градиента и его арифметические свойства
- •4°. (Здесь предполагается, что g ¹ 0 в соответствующей точке).
- •Определение дифференциалов высших порядков. Иллюстрация определения на примере дифференциалов 1-го и 2-го порядков.
- •79. Формула Тейлора для функции нескольких переменных (включая формулировку теоремы о разложимости функции по формуле Тейлора с остаточным членом в форме Пеано)
- •2) Если же второй дифференциал функции в точке является знакопеременной квадратичной формой, то точка не является точкой локального экстремума функции .
Понятие градиента и его арифметические свойства
Вектор
 называется
градиентом функции
в точке
и обозначается обычно одним из символов
называется
градиентом функции
в точке
и обозначается обычно одним из символов
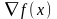 или
или
 .1°.
.1°.
 ;2°.
;2°.
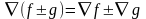 ;
;
(здесь и ниже
и
дифференцируемые в рассматриваемой
точке функции);3°.
 ;
;
4°. (Здесь предполагается, что g ¹ 0 в соответствующей точке).
Арифметические
св-ва дифференцируемых функций.
Теорема
1. Если функции
 дифференцируемы
в точке
дифференцируемы
в точке
 ,
то для любых
,
то для любых
 функция
функция
 также дифференцируемо в этой точке и
также дифференцируемо в этой точке и

 .
.
Д о к а з а т е л ь
с т в о. В силу дифференцируемости
отображений

 ,
для любых
имеем:
,
для любых
имеем:

т.е.
 при
). Таким образом, отображение
дифференцируемо в точке
и
□
при
). Таким образом, отображение
дифференцируемо в точке
и
□
Теорема
2. Если функции
 дифференцируемы
в точке
,
то функция
дифференцируемы
в точке
,
то функция
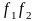 также дифференцируема в этой точке и
также дифференцируема в этой точке и
 .
.
Если, кроме того,
 ,
то дифференцируема в точке Х и функция
,
то дифференцируема в точке Х и функция
 ,
при этом
,
при этом □
□
Теорема о
дифференцировании сложной функции.
Цепное правило вычисления частных
производных сложной функции.
Теорема
3 (о
дифференцировании сложной функции ).
Пусть функции
 ,
(
,
( ),
дифференцируемы в точке
),
дифференцируемы в точке
 ,
а функция
,
а функция
 ,
,
 ,
такова, что
,
такова, что
 и дифференцируема в точке
.
Тогда сложная функция
и дифференцируема в точке
.
Тогда сложная функция
 ,
,
,дифференцируема
в точке
и
,
,
,дифференцируема
в точке
и

Замечание
1. Правило вычисления частных производных
сложной функции (1) называют цепным
правилом дифференцирования сложной
функции. Если функции
,
,
функцию
и функцию
 обозначают следующим образом
обозначают следующим образом

 ;
;
 ;то
формулу (1), опуская аргументы частных
производных, записывают, соответственно
так:
;то
формулу (1), опуская аргументы частных
производных, записывают, соответственно
так:
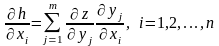 .
.
Понятие касательной
плоскости к графику функции двух
переменных и критерий ее
дифференцируемости.
Рассмотрим
функцию двух переменных
 и покажем, что ее дифференцируемость в
точке
равносильна
тому, что в точке
и покажем, что ее дифференцируемость в
точке
равносильна
тому, что в точке
 где
,
ее график имеет касательную плоскость.
где
,
ее график имеет касательную плоскость.
Говоря далее о поверхности в пространстве будем предполагать, что в окрестности каждой своей точки она представляет собой график некоторой непрерывной функции двух переменных.
Определение 1.
Пусть имеется некоторая поверхность
.
Плоскость
,
проходящая через точку
 называется касательной
плоскостью к поверхности
в
точке M0,
если расстояние от переменной точки
называется касательной
плоскостью к поверхности
в
точке M0,
если расстояние от переменной точки
 поверхности
до этой плоскости – величина бесконечно
малая высшего порядка малости при
поверхности
до этой плоскости – величина бесконечно
малая высшего порядка малости при
 ,
по сравнению с расстоянием от точки
,
по сравнению с расстоянием от точки
 до точки
до точки
 ,
т.е. если
,
т.е. если
 где
где
 – основание перпендикуляра опущенного
на плоскость
из точки
– основание перпендикуляра опущенного
на плоскость
из точки
 .
Теорема 1.
Для того, чтобы функция
,
определенная в некоторой окрестности
точки
.
Теорема 1.
Для того, чтобы функция
,
определенная в некоторой окрестности
точки
 и непрерывная в самой этой точке была
дифференцируемой в ней, необходимо и
достаточно, чтобы график функции
в точке
и непрерывная в самой этой точке была
дифференцируемой в ней, необходимо и
достаточно, чтобы график функции
в точке
 имел непараллельную оси
имел непараллельную оси
 касательную плоскость, при этом
соответствующая плоскость описывается
уравнением:
касательную плоскость, при этом
соответствующая плоскость описывается
уравнением:

(здесь
 - координаты точек касательной плоскости).
- координаты точек касательной плоскости).
Понятия частных
производных 2-го и более высоких
порядков
Пусть
функция
( )
определена в некоторой окрестности
точки
)
определена в некоторой окрестности
точки
 ,
и
,
и
 имеет
частную производную
имеет
частную производную
 по
по
 -ой
переменной. Таким образом, в окрестности
точки
определена функция
переменных
-ой
переменной. Таким образом, в окрестности
точки
определена функция
переменных
 .Если
эта функция имеет в точке
частную производную по переменной
.Если
эта функция имеет в точке
частную производную по переменной
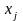 ,
то она называется второй частной
производной (или также частной производной
2-го порядка) функции
в точке
по переменным
,
то она называется второй частной
производной (или также частной производной
2-го порядка) функции
в точке
по переменным
 и
,
при этом если
и
,
при этом если
 ,
то она, соответственно, называется
второй частной производной функции
по переменной
.
Частные производные 2-го порядка по
разным переменным называются смешанными
частными производными. Частная производная
2-го порядка функции
по переменным
и
обычно обозначается одним из следующих
символов
,
то она, соответственно, называется
второй частной производной функции
по переменной
.
Частные производные 2-го порядка по
разным переменным называются смешанными
частными производными. Частная производная
2-го порядка функции
по переменным
и
обычно обозначается одним из следующих
символов
 ,
,
 или
или
 ,
,
а если , то. соответственно, – одним из символов:
 ,
,
 или
или

Точка, в которой берется та или иная вторая частная производная, часто не указывается.
Таким образом, кратко, определение второй частной производной можно ввести следующим образом:
 или
или
 .Аналогично
определяются частные производные 3-го,
4-го и более высоких порядков. Общее
определение частной производной
-го
порядка вводится индуктивно. А именно,
если уже определена частная производная
порядка
.Аналогично
определяются частные производные 3-го,
4-го и более высоких порядков. Общее
определение частной производной
-го
порядка вводится индуктивно. А именно,
если уже определена частная производная
порядка

 функции
по переменным
функции
по переменным
 и эта производная существует в некоторой
окрестности точки
,
то частная производная порядка
этой
функции по переменным
и эта производная существует в некоторой
окрестности точки
,
то частная производная порядка
этой
функции по переменным
 в
точке
определяется по правилу:
в
точке
определяется по правилу:

Теорема о смешанных
частных производных.
Теорема 1.
(теорема о смешанных частных производных)
Если частные производные
 и
и
 функции
переменных
существуют
в некоторой окрестности точки
функции
переменных
существуют
в некоторой окрестности точки
 и непрерывны в самой этой точке, то
и непрерывны в самой этой точке, то

 .
.
Понятития
раз дифференцируемой функциии и
раз непрерывно дифференцируемой
функциии.
Определение 2. Пусть
функция
определена в некоторой окрестности
точки
и имеет в этой окрестности всевозможные
частные производные
 -го
порядка
.
Тогда если все эти частные производные
дифференцируемы в точке
,
то функция
называется
раз дифференцируемой функцией в этой
точке.
-го
порядка
.
Тогда если все эти частные производные
дифференцируемы в точке
,
то функция
называется
раз дифференцируемой функцией в этой
точке.
Замечание 5.
Нетрудно
показать, что всякая
раз дифференцируемая в точке
функция является также и
раз дифференцируемой в этой точке.
Определение
3. Если функция
имеет в окрестности точки
всевозможные частные производные
 порядка
и все они непрерывны в этой точке, то
говорят что функция
раз непрерывно дифференцируема в точке
.
порядка
и все они непрерывны в этой точке, то
говорят что функция
раз непрерывно дифференцируема в точке
.
Замечание 6.
Осчевидно,
что всякая
раз непрерывно дифференцируемая в точке
функция является
раз дифференцируемой в этой точке.Если
функция
раз непрерывно дифференцируема в каждой
точке множества
 ,
то говорят, что она
раз непрерывно дифференцируема на
множестве
и пишут
,
то говорят, что она
раз непрерывно дифференцируема на
множестве
и пишут
 .
Если
,
то легко убедиться, что функция
раз дифференцируема на множестве
,
т.е.
раз дифференцируема в каждой точке
этого множества.
.
Если
,
то легко убедиться, что функция
раз дифференцируема на множестве
,
т.е.
раз дифференцируема в каждой точке
этого множества.
Вторая теорема о смешанных частных производных Пусть функция дважды дифференцируема в точке . Тогда

 ,
,
 ,т.е.всевозможные
смешанные частные производные 2-го
порядка не зависят от выбора
последовательности дифференцирования.
,т.е.всевозможные
смешанные частные производные 2-го
порядка не зависят от выбора
последовательности дифференцирования.
С учетом замечания 3(если функция имеет в некоторой окрестности точки всевозможные частные производные 2-го порядка и каждая из них непрерывна в точке , то функция дважды дифференцируема в этой точке) получим такое Следствие 1. Если функция имеет в некоторой окрестности точки всевозможные частные производные 2-го порядка и каждая из них непрерывна в точке , то имеют место равенства (1), т.е. всевозможные смешанные частные производные 2-го порядка не зависят от выбора последовательности дифференцирования.
