
- •Формула интегрирования по частям для неопределенного интеграла.
- •Основные свойства определенного интеграла Римана: интегрируемость сужения, аддитивное свойство, линейные свойства, интегрируемость произведения.
- •Число e как сумма ряда.
- •Понятие знакочередующегося ряда. Признак Лейбница. Исследование ряда
- •Понятия абсолютно и условно сходящегося числового ряда. Теорема о сходимости абсолютно сходящегося ряда.
- •Основные теоремы о степенных рядах (о непрерывности суммы степенного ряда, о почленном дифференцировании и почленном интегрировании степенного ряда)
- •Разложение функций в степенные ряды (определение).
- •Определения несобственных интегралов 1-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 1-го рода.
- •Определения несобственных интегралов 2-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 2-го рода.
- •Теорема о замене переменной и формула интегрирования по частям для несобственных интегралов.
- •Критерий сходимости несобственного интеграла от неотрицательной функции.
- •Интегральный признак сходимости числового ряда.
- •Скалярное произведение и евклидова норма в (определения). Неравенство Коши-Буняковского.
- •53. Координатные последовательности последовательности точек в . Критерий сходимости последовательности в в терминах координатных последовательностей.
- •58. Понятие функции нескольких переменных
- •Понятие градиента и его арифметические свойства
- •4°. (Здесь предполагается, что g ¹ 0 в соответствующей точке).
- •Определение дифференциалов высших порядков. Иллюстрация определения на примере дифференциалов 1-го и 2-го порядков.
- •79. Формула Тейлора для функции нескольких переменных (включая формулировку теоремы о разложимости функции по формуле Тейлора с остаточным членом в форме Пеано)
- •2) Если же второй дифференциал функции в точке является знакопеременной квадратичной формой, то точка не является точкой локального экстремума функции .
2) Если же второй дифференциал функции в точке является знакопеременной квадратичной формой, то точка не является точкой локального экстремума функции .
Понятие о задаче
на условный экстремум. Прямой метод
решения задачи на условный экстремум.
Пусть
на множестве
заданы функции
будет определена
и непрерывно дифференцируема в
некоторой окрестности точки
Замечание 1. Можно сказать, таким образом, что в точке условного экстремума функции ее градиент является линейной комбинацией градиентов функций , определяющих уравнения связи.
Д о к а з а т е л
ь с т в о. Установленные ранее необходимые
условия относительного экстремума
(4) и (6) означают, что каждый из последних
является линейной комбинацией первых ее столбцов, которые по условию линейно независимы. Следовательно, ранг этой матрицы равен . Поэтому первая ее строка является линейной комбинацией остальных строк □ При исследовании задачи на условный экстремум обычно вводят вспомогательную функцию
от
а равенства
Таким образом,
из теоремы 1 вытекает такое Следствие.
Пусть
функции
и
(
)
непрерывно дифференцируемы в некоторой
окрестности точки
и в этой точке ранг матрицы Якоби
системы функций
равен
.
Тогда если
– точка условного экстремума функции
при
наличии связей (1), то найдутся такие
вещественные числа
Тогда если
квадратичная форма
Мера Жордана
в пространстве
.
Определение
1. Точка
Ясно, что двумерный брус представляет собой прямоугольник на плоскости. Трехмерный брус называют параллелепипедом. Иногда вместо термина n-мерный брус используется термин n-мерный прямоугольник или n-мерный параллелепипед. По определению объемом -мерного бруса называется вещественное число
Свойства меры Жордана 1 (Свойство неотрицательности). Мера Жордана любого измеримого по Жордану множества неотрицательна. 2 (Свойство полноты) Всякое подмножество множества жордановой меры нуль измеримо по Жордану и имеет жорданову меру нуль. 3 (Измеримость пустого множества) Пустое множество измеримо по Жордану и имеет жорданову меру нуль. 4 (Критерий измеримости). Для того, чтобы ограниченное множество было измеримо по Жордану, необходимо и достаточно, чтобы граница этого множества имела Жорданову меру нуль
5. (Измеримость
графика непрерывной на компакте
функции) График
всякой непрерывной на компакте
функции
имеет Жорданову меру нуль (в пространстве
6. (Замкнутость
класса измеримых множеств относительно
основных операций). Множество
всех измеримых по Жордану множеств
замкнуто относительно операций
объединения, разности и пересечения,
т.е. если множества
7. (Мера объединения конечного числа множеств меры нуль) Объединение любого конечного числа множеств жордановой меры нуль измеримо по Жордану и имеет жорданову меру нуль. 8. (Обобщенное свойство аддитивности). Пусть множества и измеримы по Жордану. Тогда если их пересечение имеет жорданову меру нуль, то
9. (Свойство аддитивности). Если множества и – измеримы по Жордану и их пересечение пусто, то справедливо равенство (1).
10. (Свойство
монотонности).
Если множества
Понятие кратного
интеграла
Определение
1. Совокупность
1) каждое из множеств , , измеримо по Жордану; 2) множества , , попарно пересекаются разве лишь по своим границам;
3)
Диаметром
ограниченного множества
называется число
Первая из них
называется нижней суммой Дарбу функции
соответствующей разбиению
Свойства кратных интегралов
Отметим некоторые
свойства сумм Дарбу. Условимся говорить,
что разбиение
Свойство 1. При
измельчении разбиения нижние суммы
Дарбу не убывают, а верхние суммы Дарбу
не возрастают, т.е. если разбиение
мельче разбиения
,
то
Свойство 2.
Любая нижняя сумма Дарбу не превосходит
любой верхней суммы Дарбу, т.е. для
любых двух разбиений
и
множества
имеет место неравенство
интегрируемые по Риману функции переменных обладают следующими свойствами:
1*. Если
Замечание 1. Предыдущие два свойства называются л и н е й н ы м и свойствами двойного интеграла.
3*.
Если
,
,
и
6* (Теорема
о среднем). Пусть
и
причем
7*. (Аддитивное
свойство). Если
Сведение двойного интеграла к повторному: случай пря моугольника
Пусть функция
двух переменных
и
(
)
определена на прямоугольнике
Замечание 1.
Если в формулировке теоремы 1
и
поменять ролями, т.е. наряду с условием
Предположения
теоремы 1 и ее аналога, упомянутого в
замечании 1 заведомо выполняются, если
функция
непрерывна на прямоугольнике
.
Поэтому справедлива следующая Теорема
2. Пусть
функция
непрерывна на прямоугольнике
.
Тогда оба
повторных интеграла
и
существуют
и равны двойному интегралу
Сведение двойного интеграла к повторному: случай элементарной области.
Пусть функции
(
.Тогда существует и повторный интеграл , при этом имеет место равенство
Следствие.
Если функция
непрерывна на множестве
то
справедлива формула (4), при этом оба
интеграла в ней (двойной и повторный)
заведомо существуют. Замечание
2. Если в
формулировке теоремы 2
и
поменять ролями и наряду с условием
Как и выше эта формула заведомо справедлива, если функция непрерывна на множестве .
Сведение тройного и общего кратного интеграла к повторному.
Пусть
называется элементарным относительно оси или также областью элементарной относительно этой оси.
Теорема 4.
Если функция
Аналогично вводятся понятия области трехмерного пространства, элементарной относительно оси и области, элементарной относительно оси . Для таких областей справедливы теоремы аналогичные теореме 3.Ясно теперь как обобщается эта теорема на общий n-мерный случай.Пусть - замкнутое, измеримое по Жордану множество, а и непрерывные на нем функции. Тогда (измеримое по Жордану!) множество
называется
элементарной
относительно оси
Теорема о замене переменных в кратном интеграле.
Теорема 1. Пусть
функция f (двух переменных) интегрируема
по Риману на измеримой по Жордану
области
обладающим следующими свойствами:
Отображение
взаимно-однозначно отображает
на
2. Координатные
функции отображения
 интегрируема на множестве
(здесь
интегрируема на множестве
(здесь
 ,
,
 - якобиан отображения
)
и имеет место равенство
- якобиан отображения
)
и имеет место равенство
Несобственные кратные интегралы
Последовательность
1о.
Каждое из множеств
2о.
Пусть функци ( ) определена на множестве и интегрируема на любом замкнутом, измеримом по Жордану подмножестве множества .
Определение
1. Если для
любой исчерпывающей множество
последовательности множеств
существует конечный предел
и этот предел не
зависит от выбора исчерпывающей
последовательности, то его называют
несобственным двойным интегралом
функции
на множестве
и обозначают тем же символом, что и
обычный («собственный») двойной
интеграл
Если условия этого определения выполнены то говорят, что интеграл (2) сходится. В противном случае говорят, что этот интеграл расходится.
Теорема 1. Для
сходимости несобственного двойного
интеграла (2) от неотрицательной на
множестве
функции
необходимо и достаточно, чтобы хотя
бы для одной исчерпывающей множество
последовательности
Следствием
теоремы 1 является следующая Теорема
2 (признак
сравнения). Пусть функции
и
интегрируемы
по Риману на любом замкнутом измеримом
по Жордану подмножестве открытого
множества
и
сходится, то сходится и несобственный интеграл
Если же интеграл
(5) расходится, то расходится и интеграл
(4).Коснемся, кратко, абсолютной
сходимости, несобственных двойных
интегралов. Пусть функция
Определение
2. Несобственный
интеграл
называется
абсолютно сходящимся, если сходится
интеграл
Интеграл Пуассона.
Вычислим интеграл
Отсюда, с учетом теоремы 1 следует, что
Выберем теперь
в качестве исчерпывающей плоскость
последовательности
Тогда
|
|
|||||||||||||||||||||||||||||||||||||||

 ,
,
 ,
а также функция
.
Задача об отыскании экстремума
(максимума или минимума) функции
на множестве
,
а также функция
.
Задача об отыскании экстремума
(максимума или минимума) функции
на множестве
 ,т.е.
на множестве всех решений
,т.е.
на множестве всех решений
 системы
уравнений,
системы
уравнений,
 называется задачей на условный или
относительный экстремум. Уравнения
системы (1) часто называют уравнениями
связи или просто связями. В связи с
этим соответствующую задачу на условный
экстремум называют задачей на экстремум
функции
при наличии связей (1). Определение
1. Точка
называется задачей на условный или
относительный экстремум. Уравнения
системы (1) часто называют уравнениями
связи или просто связями. В связи с
этим соответствующую задачу на условный
экстремум называют задачей на экстремум
функции
при наличии связей (1). Определение
1. Точка
 градиенты
градиенты
 функций
функций
 линейно независимы. Если из этих
градиентов как из строк составить
матрицу
линейно независимы. Если из этих
градиентов как из строк составить
матрицу ,называемую
матрицей Якоби системы функций
в точке
,
то ранг этой матрицы будет равен
(т.к.
ее строки линейно независимы). Как
известно из курса алгебры ранг матрицы,
в то же время, равен наивысшему порядков
тех ее миноров, которые отличны от
нуля. Так как ранг матрицы Якоби
,называемую
матрицей Якоби системы функций
в точке
,
то ранг этой матрицы будет равен
(т.к.
ее строки линейно независимы). Как
известно из курса алгебры ранг матрицы,
в то же время, равен наивысшему порядков
тех ее миноров, которые отличны от
нуля. Так как ранг матрицы Якоби
 равен
,
то без ущерба для общности можно
считать, что минор порядка
,
расположенный в первых
ее столбцах отличен от нуля:
равен
,
то без ущерба для общности можно
считать, что минор порядка
,
расположенный в первых
ее столбцах отличен от нуля:
 ,
т.е. выразить их через остальные
переменные:
,
т.е. выразить их через остальные
переменные:

 .
Наконец, оказывается, что точка
является точкой условного экстремума
функции
при наличии связей (1) тогда и только
тогда, когда точка
является
точкой локального экстремума функции
.
.
Наконец, оказывается, что точка
является точкой условного экстремума
функции
при наличии связей (1) тогда и только
тогда, когда точка
является
точкой локального экстремума функции
.
 и в этой точке ранг матрицы Якоби
системы функций
равен
.
Тогда если
– точка условного экстремума функции
при
наличии связей (1), то найдутся такие
вещественные числа
и в этой точке ранг матрицы Якоби
системы функций
равен
.
Тогда если
– точка условного экстремума функции
при
наличии связей (1), то найдутся такие
вещественные числа
 ,
что
,
что .
. столбцов матрицы
столбцов матрицы

 переменных
переменных
 .
Ее называют функцией Лагранжа, числа
.
Ее называют функцией Лагранжа, числа
 – множителями Лагранжа, а метод
отыскания точек условного экстремума,
в котором используется эта функция
называется методом множителей Лагранжа.
Для его описания заметим, что из
определения функции Лагранжа следует,
что если положить
– множителями Лагранжа, а метод
отыскания точек условного экстремума,
в котором используется эта функция
называется методом множителей Лагранжа.
Для его описания заметим, что из
определения функции Лагранжа следует,
что если положить
 и
и
 ,
то векторное равенство (7) равносильно
следующей системе скалярных равенств
,
то векторное равенство (7) равносильно
следующей системе скалярных равенств
 которые
необходимо должны выполняться, если
– точка условного экстремума функции
при
наличии связей (1), могут быть записаны
в виде:
которые
необходимо должны выполняться, если
– точка условного экстремума функции
при
наличии связей (1), могут быть записаны
в виде:
 ,
что точка
,
что точка
 является
стационарной точкой функции Лагранжа
(8), т.е. удовлетворяет условиям (9) и
(10). Достаточные
условия относительного экстремума:
Пусть
функции
является
стационарной точкой функции Лагранжа
(8), т.е. удовлетворяет условиям (9) и
(10). Достаточные
условия относительного экстремума:
Пусть
функции
 дважды непрерывно дифференцируемы в
некоторой окрестности точки
,
дважды непрерывно дифференцируемы в
некоторой окрестности точки
,

 и точка
вместе с некоторым вектором
и точка
вместе с некоторым вектором удовлетворяет системе уравнений
удовлетворяет системе уравнений


 -
положительно определенная (отрицательно
определенная) на подпространстве
решений системы линейных уравнений
-
положительно определенная (отрицательно
определенная) на подпространстве
решений системы линейных уравнений ,
то функция
имеет в точке
строгий условный локальный минимум
(соотв., максимум) при наличии связей
(1), если же на этом подпространстве
она знакопеременная, то функция
в точке
не имеет условного экстремума.
,
то функция
имеет в точке
строгий условный локальный минимум
(соотв., максимум) при наличии связей
(1), если же на этом подпространстве
она знакопеременная, то функция
в точке
не имеет условного экстремума. называется граничной точкой множества
называется граничной точкой множества
 если в любой ее окрестности имеются
как точки, принадлежащие этому
множеству, так и точки ему не
принадлежащие. Множество всех граничных
точек множества
называется границей этого множества
и обозначается символом
если в любой ее окрестности имеются
как точки, принадлежащие этому
множеству, так и точки ему не
принадлежащие. Множество всех граничных
точек множества
называется границей этого множества
и обозначается символом
 .Определение
2. Множество
.Определение
2. Множество
 называют (замкнутым)
-мерным
брусом или, короче, брусом в
.
называют (замкнутым)
-мерным
брусом или, короче, брусом в
. Определение
3. Множество
в пространстве
называется элементарным, если оно
представляет собой объединение
конечного числа брусов в
,
любые два из которых пересекаются
разве лишь по своим границам.Хотя одно
и то же элементарное множество
разными способами можно представить
в виде объединения конечного числа
-мерных
брусов, попарно пересекающихся разве
лишь по своим границам, сумма объемов
этих брусов будет одной и той же и ее
естественно назвать объемом элементарного
множества
.
Таким образом, если
– элементарное множество и
Определение
3. Множество
в пространстве
называется элементарным, если оно
представляет собой объединение
конечного числа брусов в
,
любые два из которых пересекаются
разве лишь по своим границам.Хотя одно
и то же элементарное множество
разными способами можно представить
в виде объединения конечного числа
-мерных
брусов, попарно пересекающихся разве
лишь по своим границам, сумма объемов
этих брусов будет одной и той же и ее
естественно назвать объемом элементарного
множества
.
Таким образом, если
– элементарное множество и ,где
,где
 (
)
– брусы, которые попарно пересекаются
разве лишь по своим границам, то
-мерным
его объемом называется вещественное
число
,
которое находится по формуле
(
)
– брусы, которые попарно пересекаются
разве лишь по своим границам, то
-мерным
его объемом называется вещественное
число
,
которое находится по формуле .Класс
всех элементарных множеств, пространства
,
обозначим
.Класс
всех элементарных множеств, пространства
,
обозначим
 .
Для произвольного ограниченного
множества
.
Для произвольного ограниченного
множества
 числа
и
называют,
соответственно, внешней и внутренней
мерой Жордана множества
( в первой из этих формул точная нижняя
грань берется по всем элементарным
множествам
содержащих множество
,
а во второй из этих формул точная
верхняя грани берется по всем
элементарным множествам
которые содержатся во множестве
).Определение
4. Пусть
– ограниченное множество. Множество
называется измеримым по Жордану, если
его внешняя и внутренняя меры равны
между собой, при этом число
называется
мерой Жордана множества
или, также,
-мерным
объемом этого множества.
числа
и
называют,
соответственно, внешней и внутренней
мерой Жордана множества
( в первой из этих формул точная нижняя
грань берется по всем элементарным
множествам
содержащих множество
,
а во второй из этих формул точная
верхняя грани берется по всем
элементарным множествам
которые содержатся во множестве
).Определение
4. Пусть
– ограниченное множество. Множество
называется измеримым по Жордану, если
его внешняя и внутренняя меры равны
между собой, при этом число
называется
мерой Жордана множества
или, также,
-мерным
объемом этого множества. )
) и
и
 измеримы по Жордану, то их объединение
измеримы по Жордану, то их объединение
 ,
разность
,
разность
 и пересечение
и пересечение
 измеримы по Жордану.
измеримы по Жордану.
 и
и
 измеримы по Жордану и
измеримы по Жордану и
 ,
то
,
то
 .
.
 множеств
множеств
 ,
,
 ,
называется разбиением измеримого по
Жордану множества
,
если
,
называется разбиением измеримого по
Жордану множества
,
если ■
■ (здесь
(здесь
 –евклидово расстояние в
).
Соответственно, рангом разбиения
измеримого по Жордану множества
называется число
–евклидово расстояние в
).
Соответственно, рангом разбиения
измеримого по Жордану множества
называется число
 Пусть
теперь на измеримом по Жордану множестве
задана функция
Пусть
теперь на измеримом по Жордану множестве
задана функция
 .
Выберем какое-нибудь разбиение
множества
.
Для любого
положим
.
Выберем какое-нибудь разбиение
множества
.
Для любого
положим
 ,
,
 (в
предположении ограниченности функции
эти числа конечны) и рассмотрим две
суммы
(в
предположении ограниченности функции
эти числа конечны) и рассмотрим две
суммы
 и
и
 .
. множества
,
а вторая, соответственно, – верхней
суммой Дарбу этой функции, соответствующей
тому же разбиению.
множества
,
а вторая, соответственно, – верхней
суммой Дарбу этой функции, соответствующей
тому же разбиению.
 множества
мельче разбиения
множества
мельче разбиения
 того же множества (или, что первое из
этих разбиений является измельчением
второго), если каждое из множеств
разбиения
того же множества (или, что первое из
этих разбиений является измельчением
второго), если каждое из множеств
разбиения
 является объединением некоторых из
множеств разбиения
является объединением некоторых из
множеств разбиения
 .
. ,
а
,
а
 .
. .
. ,
то
,
то

 и
и 2*.
Если
и
,
то
2*.
Если
и
,
то
 ,
при этом
,
при этом .
. ,
то
,
то .В
частности, если
и
.В
частности, если
и
 ,
то
,
то .4*.
Если
и
,
то
.4*.
Если
и
,
то
 5*.
Если
,
то
5*.
Если
,
то
 ,
при этом
,
при этом

 ,
,

 .
Тогда существует такое
.
Тогда существует такое
 ,
что
,
что
 ,
,
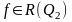 и
и
 (в частности,
(в частности, ),
то
),
то
 и
и 8*.
Если функции
и
определены на множестве
8*.
Если функции
и
определены на множестве
 и отличаются на нем лишь на множестве
и отличаются на нем лишь на множестве
 ,
имеющем жорданову меру нуль, то из
интегрируемости по Риману одной из
них на множестве
следует интегрируемость по Риману и
другой, причем
,
имеющем жорданову меру нуль, то из
интегрируемости по Риману одной из
них на множестве
следует интегрируемость по Риману и
другой, причем
 и для каждого фиксированного
и для каждого фиксированного
 функция
функция
 одной переменной
одной переменной
 интегрируема по Риману на отрезке
интегрируема по Риману на отрезке
 ,
и, следовательно, для каждого
фиксированного
существует обычный определенный
интеграл Римана
,
и, следовательно, для каждого
фиксированного
существует обычный определенный
интеграл Римана .Тогда
если функция
.Тогда
если функция
 одной переменной
интегрируема по Риману на отрезке
,
то интеграл
одной переменной
интегрируема по Риману на отрезке
,
то интеграл называется
повторным интегралом от функции
на прямоугольнике и обычно обозначается
называется
повторным интегралом от функции
на прямоугольнике и обычно обозначается Поменяв
ролями
и
в предыдущем определении получим
определение повторного интеграла
другого типа.
Поменяв
ролями
и
в предыдущем определении получим
определение повторного интеграла
другого типа.
 Этот
повторный интеграл обозначается,
символом
Этот
повторный интеграл обозначается,
символом .Теорема
1. Пусть
функция
интегрируема на прямоугольнике
и для любого
существует определенный интеграл
Римана
Тогда
существует и повторный интеграл
,при
этом имеет место равенство
.Теорема
1. Пусть
функция
интегрируема на прямоугольнике
и для любого
существует определенный интеграл
Римана
Тогда
существует и повторный интеграл
,при
этом имеет место равенство .
. предположить существование интеграла
предположить существование интеграла
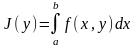 при любом
,
то вместо формулы (1) получим следующую
формулу
при любом
,
то вместо формулы (1) получим следующую
формулу .
.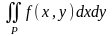
 )
и
)
и
 (
( )
определены и непрерывны на отрезке
и
)
определены и непрерывны на отрезке
и

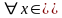 Далее,
пусть функция
определена на криволинейной трапеции
Далее,
пусть функция
определена на криволинейной трапеции ее называют областью
элементарной
относительно оси
ее называют областью
элементарной
относительно оси
 - и при любом
- и при любом
 существует определенный интеграл
существует определенный интеграл
 .Тогда
если определенная этим равенством
функция
одной переменной
интегрируема по Риману на отрезке
,
то интеграл
.Тогда
если определенная этим равенством
функция
одной переменной
интегрируема по Риману на отрезке
,
то интеграл называется
повторным интегралом от функции
по указанной выше криволинейной
трапеции
.
Этот повторный интеграл часто
обозначается так
называется
повторным интегралом от функции
по указанной выше криволинейной
трапеции
.
Этот повторный интеграл часто
обозначается так
 Аналогично
на криволинейной трапеции
Аналогично
на криволинейной трапеции (здесь
функции
(здесь
функции
 и
и
 непрерывны на отрезке
и
непрерывны на отрезке
и

 ),называемой
также областью
элементарной относительно оси
),называемой
также областью
элементарной относительно оси
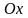 ,
определяется повторный интеграл
,
определяется повторный интеграл
 в котором по сравнению с предыдущим
повторным интегралом переменные
и
меняются ролями.Отметим, что непрерывность
функций
и
гарантирует измеримость области
,
а непрерывность функций
и
в котором по сравнению с предыдущим
повторным интегралом переменные
и
меняются ролями.Отметим, что непрерывность
функций
и
гарантирует измеримость области
,
а непрерывность функций
и
 - измеримость
.Теорема
3. Пусть
функция
интегрируема
по Риману на криволинейной трапеции
и при любом
существует определенный интеграл
- измеримость
.Теорема
3. Пусть
функция
интегрируема
по Риману на криволинейной трапеции
и при любом
существует определенный интеграл .
. ,
где
,предположить
существование интеграла
,
где
,предположить
существование интеграла
 при любом
,
то вместо формулы (4) получим еще одну
формулу сведения двойного интеграла
к повторному:
при любом
,
то вместо формулы (4) получим еще одну
формулу сведения двойного интеграла
к повторному: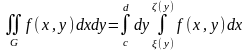 .
. -
замкнутое, измеримое по Жордану
множество и функции
-
замкнутое, измеримое по Жордану
множество и функции
 и
и
 непрерывны на нем, причем
непрерывны на нем, причем
 .
Множество
.
Множество
 непрерывна в области
непрерывна в области
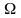 элементарной
относительно оси
,
то
элементарной
относительно оси
,
то


 областью.
Теорема 5.
Если
областью.
Теорема 5.
Если
 - элементарная
относительно оси
область,
а функция
- элементарная
относительно оси
область,
а функция
 - непрерывная в ней функция, то
- непрерывная в ней функция, то

 ,
которая является образом измеримой
по Жордану области
при отображении
,
которая является образом измеримой
по Жордану области
при отображении
 (G – область),
(G – область), .
. непрерывны на замыкании
непрерывны на замыкании
 области
и имеют непрерывные на
частные производные первого порядка
по всем переменным.
области
и имеют непрерывные на
частные производные первого порядка
по всем переменным.
 ,
открытых множеств
,
открытых множеств
 ,
,
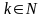 ,
называется исчерпывающей множество
,
если она обладает следующими свойствами:
,
называется исчерпывающей множество
,
если она обладает следующими свойствами: ,
,
измеримо по Жордану;
,
,
измеримо по Жордану; ,
(
,
( – замыкание множества
);3о.
– замыкание множества
);3о.
 .
.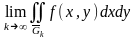

 ,
была ограничена числовая последовательность
,
была ограничена числовая последовательность
 на
множестве
.
Тогда если несобственный интеграл
на
множестве
.
Тогда если несобственный интеграл

 ,
,
интегрируема по Риману на любом
замкнутом, измеримом по Жордану
подмножестве открытого множества
.
,
,
интегрируема по Риману на любом
замкнутом, измеримом по Жордану
подмножестве открытого множества
. Теорема
3. Несобственный
интеграл
сходится
тогда и только тогда, когда он сходится
абсолютно.
Теорема
3. Несобственный
интеграл
сходится
тогда и только тогда, когда он сходится
абсолютно. где
где
 .
В качестве исчерпывающей это множество
последовательности
выберем следующую последовательность
открытых кругов
.
В качестве исчерпывающей это множество
последовательности
выберем следующую последовательность
открытых кругов Переходя
к полярным координатам, и сводя затем
двойной интеграл к повторному, получим
Переходя
к полярным координатам, и сводя затем
двойной интеграл к повторному, получим
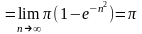 .
. последовательность квадратов
последовательность квадратов
 .
. Переходя
здесь к пределу при
и используя равенство (7) получим
Переходя
здесь к пределу при
и используя равенство (7) получим Таким
образом,
Таким
образом,
 Этот
интеграл называется интегралом
Пуассона и широко используется в
теории вероятностей
Этот
интеграл называется интегралом
Пуассона и широко используется в
теории вероятностей