Линейные уравнения с постоянными коэффициентами.

Определение: Линейным дифференциальным уравнением второго порядка называется уравнения вида:

yⁿ+p(x)y'+q(x)y=f(x), где у- искомая функция, p(x),q(x) и f(x)- известные функции непрерывные на некотором интервале (a,b).

Если f(x)=0, то уравнение называется линейным однородным уравнением, в противном случае оно называется линейным неоднородным уравнением. В этом разделе мы рассмотрим важный и распространенный случай, когда уравнение вида функции p(x) и q(x)- постоянные величины. Уравнение такого вида называется линейными уравнениями с постоянными коэффициентами. Итак, мы рассматриваем уравнения вида: у``+ py`+q`=f(x), где p и q- вещественные числа. Далее мы будем иметь дело только с уравнениями такого типа.

Линейное однородное уравнение.

у``+ py`+q`=0, где p и q- вещественные числа. Линейное дифференциальное уравнение второго порядка может иметь множество решений. Однако среди них выделяется базисные решения, по которым строится общее решение уравнения. Таких решений для уравнения второго порядка два- каков порядок уравнения, будем искать решение уравнения в виде у= e^kx , где k-некоторое число. Подставляя эту фунцию в уравнение, получаем:

k² e^kx+ pke^kx+q e^kx=0.Сокращая обе части равенства на e^kx, получаем квадратное уравнение относительно k: k²+ pk+q =0. Уравнение называется характеристическим уравнением для дифференциального уравнения.

Вид общего уравнения существенно зависит от того, какие корни имеет характеристическое уравнение. Обозначим эти корни через k₁ и k₂. Эти корни характеристического уравнения вещественные и k₁ ≠k₂., то общее решение однородного дифференциального уравнения имеет вид:

у=С₁e^k1x+ С₂ e^k2x. Эти корни уравнения вещественные и равны (k₁ =k₂=k), то общее решение уравнения имеет вид: у=С₁e^kx+ С₂ х e^kx. Если корни характеристического уравнения комплексные (k₁ =a+b_i, k₂= a-b_i, где i= - мнимая единица, a и b – вещественные числа), то общее решение имеет вид:

у= e^аx(С₁cos bx+ С₂ sin bx), где а=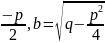 . Во всех случаях 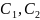- произвольные постоянные.

Пример:

y``=5y`+4=0. Его корни вещественные и различны k₁ =1, k₂=4 -> общее решение данного уравнения имеет вид: у=С₁e^x+ С₂ e^4x.

Лекция 12. Решение примеров:

Пример: y``-6y`+9=0.

Решение: Составим уравнение характеристическое уравнение

k²-6k+9=0 или (k-3) ²=0

Оно имеет кратный корень k =3, следовательно, общее решение данного однородного уравнения имеет вид:

y= e^3x(С₁+ С₂x)

Пример:

y``-2y`+2y=0.

Решение: Соответствующее характеристическое уравнение

k²-2k+2=0

Имеет дискриминант равный -1, и значит, комплексно-сопряженные корни

k₁=1+i, k₂=1-i, где

Следовательно, общее решение данного уравнения имеет вид:

y= e^x (С₁ sin x+ С₂ cos x)

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Рассмотрим линейное неоднородное уравнение второго порядка

y``+py`+qy=f(x) (1) , где p и q- вещественные числа, f(x) непрерывная функция.

Как известно общее решение такого уравнения представляет собой сумму частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения.

у _{общее неоднородное.}= у _{Частное однородное} + у _{общее. однородное}

Общее решение однородного уравнения мы находить умеем, поэтому остается рассмотреть вопрос о нахождении частного решения. Для нахождения частного решения можно применить метод вариации произвольных постоянных. Однако если в правой части уравнения (1) - многочлен, либо показательная функция, либо тригонометрическая функция sin βx или cos βx, либо линейная комбинация перечисленных функций, то частное решение может быть найдено методом неопределенных коэффициентов, не содержащим процесса интегрирования.

Рассмотрим различные случаи правых частей уравнения y" + py' + qy = f(x).

1)   Правая часть имеет вид   F(x) = P_n(x),   где P_n(х)=a₀xⁿ+ a₁x^n-1+ a_n-1x+ a_n – многочлен степени n. Тогда частное решение у можно искать в виде y= Q_n (x) x^r , где Q_n (x) – многочлен той же степени, что и P_n (х), а r – число корней характеристического уравнения, равных нулю.

Пример.

Найти   общее   решение   уравнения   у" – 2у' + у = x+1.

Решение:

 Общее решение соответствующего однородного уравнения имеет вид у= е^х (C₁ + C₂x)

Так как правая часть уравнения- многочлен первой степени и ни один из корней характеристического уравнения k² – 2k + 1 = 0 не равен нулю (k₁ = k₂ = 1), то частное решение ищем в виде, у = (Ах + В)х⁰=Ах+В, где А и В – неизвестные коэффициенты.

Дифференцируя дважды у = Ах + В и подставляя, у, у' и у" в данное уравнение, найдем

–2А + Ах + В = х + 1.

Приравнивая коэффициенты при одинаковых степенях х в обеих частях равенства: А = 1, –2А + В = 1, – находим: А = 1, В = 3.

Итак, частное решение данного уравнения имеет вид у = х + 3, а его общее решение у = е^х(C₁ + C₂x)+(х + 3)

2)  Правая часть имеет вид  f(x) = e^αx P_n(х),  где P_n(х) – многочлен степени n. Тогда частное решение следует искать в виде y= Q_n (x) x^rе^αх, где Q_n(x) – многочлен той же степени, что и P_n(х), а r — число корней характеристического уравнения, равных а. Если а= 0, то f(х) = P_n(х), т. е. имеет место случай 1.