Лекция 9.

где C - произвольная постоянная. Тогда искомое общее решение линейного неоднородного уравнения имеет вид: [ ]

Линейные уравнения первого порядка можно интегрировать также методом Бернулли, С помощью подстановки y = uv , где u и v - две неизвестные функции, исходное уравнение преобразуется к виду

u′v + vu ′ + P(x)uv = Q(x) , или u[v′ + P(x)v] + uv ′ = Q(x)

Пользуясь тем, что одна из неизвестных функций (например,v ) может быть выбрана совершенно произвольно (поскольку лишь произведение uv должно удовлетворять исходному уравнению), за v

принимают любое частное решение уравнения v′ + P(x)v = 0 (например, ) обращающее, следовательно, в нуль коэффициент при u в последнем уравнении. Тогда предыдущее уравнение примет вид: vu′ = Q(x) или

т. е.

откуда:

Общее решение исходного уравнения находится умножением u на v

[ ]

Уравнение (линейное) вида:

, где m≠0, m≠1, называется уравнением Бернулли.

Его можно в линейное уравнение, производя замену независимой функции при помощи подстановки z=y^1-m, в результате чего исходное уравнение преобразуется к виду:

При интегрировании конкретных уравнений Бернулли их не надо предварительно преобразовывать в линейные, а сразу применять либо метод Бернулли, либо метод вариации произвольной постоянной.

Пример:

Найти общее решение уравнения

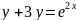
Решение: данное уравнение является линейным, здесь P(x)=3,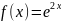

Решаем сначала соответствующее однородное уравнение Разделяя переменные 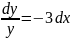интегрируя находим 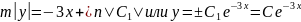общее решение данного уравнение в виде 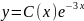. Дифференцируя уравнение, имеем: 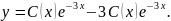Подставляя в данное уравнение выражение для y и y` получаем: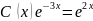 , 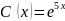или , откуда произвольная постоянная. Следовательно, общее решение данного уравнения имеет вид: 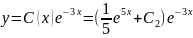или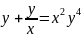

Это уравнение Бернулли. Проинтегрируем его по методу вариации произвольной постоянной. Для этого интегрируем сначала соответствующее линейное уравнение 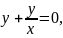решение которого 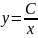Ищем решение исходного уравнения Бернулли 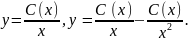Подстановка y и y` в уравнение дает или

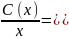
Интегрируем полученное уравнение

=

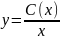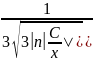
Пример:

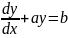, где a и b- постоянные.

Подстановка:

y=u (x)v(x)

Разделяем переменные:

dy= (-ay+b)dx

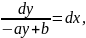
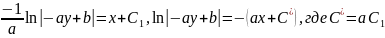
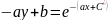
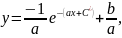
или окончательно , где обозначено 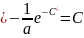это и есть общее решение уравнения.

Дифференциальные уравнения второго порядка.

y′′ = f (x,y,y`).

Начальными условиями при х=х₀ для решения будут условия y=y₀ , y`=y`_0. Геометрический смысл:

Через заданную точку плоскости (х_0, y₀) с заданным с тангенсом угла наклона касательной y`₀ проходит единственная кривая.

Лекция 10.

Рассмотрим, например, уравнение:

у``=2. Это уравнение второго порядка. Так как функции f (x,y,y`)=2. f<sub>y</sub>(x,y,y`)= 0 и f<sub>y`</sub> (x,y,y`)=0. Определена и непрерывна во всем пространстве переменных (x,y,y`), то оно удовлетворяет во всем пространстве требования Коши.

Общее решение данного уравнения найдем двукратным последова­тельным интегрированием. Последовательно интегрируя, находим сна­чала первую производную. y` = 2x + C₁, а затем и общее решение: y = x² + C₁x + C₂, где C₁ и C₂ - произвольные постоянные.

Геометрически общее решение представляет собой семейство парабол, причем, так как оно зависит от двух произвольных постоянных, то через каждую точку плоскости проходит бесконечное множество парабол, имеющих различные касательные в этой точке.

Поэтому для выделения одной параболы из полученного семейства кроме точки (x₀, y₀), через которую проходит парабола, нужно задать еще угловой коэффициент (y₀) касательной к параболе в этой точке.

Н айдем частное решение данного уравнения при начальных условиях y|_x=1=1, y`|_x=1=1. Подставляя эти значения в выражения для общего решения  y = x²+C₁x+C₂ и его производной y = 2x+C₁ для определения C₁ и C₂, получаем систему уравнений  1 = 1 + C₁ + C₂ 1 = 2 + C₁. Отсюда находим C₁ = -1 и C₂ = 1. Следовательно, частным решением является функция:  y = x² - x + 1, график которой - парабола, проходящая через точку (1, 1) с угловым коэффициентом в этой точке, равным единице.