Лекция 8.

Однородные уравнения первого порядка.

Уравнение вида Р(x,y) dx+Q(x,y) dy=0 называется однородным, если Р(x,y) и Q(x,y)- однородные функции одного измерения. Функция f(x,y) называется однородной измерения m, если f(λx , λy)= λ^m(x,y)

Однородное уравнение может быть приведено к виду y`=f(x/y). С помощью подстановки y = tx однородное уравнение приводится к уравнению с разделяющимися переменными по отношению к новой неизвестной функции t.

Пример 1: Найти общий интеграл дифференциального уравнения:

(x²+2xy)dx+xydy=0

Здесь Р(x,y)= (x²+2xy) и Q(x,y)= xy.

Обе функции однородные второго измерения. Введем подстановку y = tx, откуда dy=xdt+tdx, тогда уравнение примет вид:

x²+2 x² t +t x²(xdt+tdx)=0 или

(x²+2 x² t +t²x²) dx +tx³dt=0

Разделяя переменные и интегрируя, имеем:

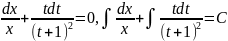
Преобразуем второй интеграл:

Возвращаясь к прежней неизвестной функции y(t=y/x) получаем ответ: 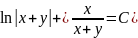(Общий интеграл)

Дифференциальные уравнение приводящиеся к однородным.

Уравнения вида 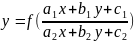при 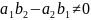приводится к однородному, подстановкой

x = u + a, y = v + β , где постоянные α и β- точка пересечения прямых:

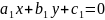и

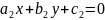
Если же 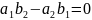, то подстановка позволяет разделить переменные.

Пример 2. Найти общий интеграл уравнения:

(2x+y+1) dx + (x+2y-1) dy=0

Уравнение принадлежит к первому типу, поскольку:

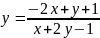
4 | 2 1|=3≠0

| 1 2|

Находим точку пересечения прямых 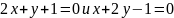имеем x= a= -1 , y=β=1. Производим в исходном уравнение замену переменных, полагая x = u + a= u-1, y = v + 1, dx=du, dy=dv. Уравнение преобразуется к виду:

(24+v)du + (u+2v)=dv=0

В полученном однородном уравнение:

V=ut, откуда dv=udt

ttdu придем к уравнению с разделяющимися переменными 2(t²+t+1)udu+u²(tt2t)dt=0 общий интеграл которого есть 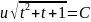или после замены t=v/u и возведения в квадрат u²+uv+v²=c²

Возвращаясь к переменным x и y (u=x+1, v=y-1)после элементарных преобразований найдем общий интеграл исходного уравнения x²+y²+xy+x-y=C₁ (Здесь положено C₁= С²-1)

Линейные дифференциальные уравнения первого порядка.

Уравнение вида y′ + P(x) y = Q(x) называется линейным ( y и y′ входят в первых степенях, не перемножаясь между собой). Если Q(x) ≠ 0, то уравнение называется линейным неоднородным, а если Q(x) = 0 - линейным однородным. Общее решение однородного уравнения y′ + P(x) y =0 получается разделением переменных: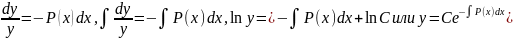

где C -произвольная постоянная.

Общее решение линейного неоднородного уравнения можно найти исходя из общего решения соответствующего однородного уравнения методом Лагранжа, варьируя произвольную постоянную, т. е. полагая где C(x) -некоторая, подлежащая определению, дифференцируемая функция от x

Для нахождения C(x) нужно подставить y в исходное уравнение, что приводит к уравнению: 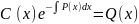Отсюда 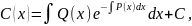где C - произвольная постоянная. Тогда искомое общее решение линейного неоднородного уравнения имеет вид: [ ]

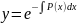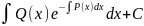Линейные уравнения первого порядка можно интегрировать также методом Бернулли, С помощью подстановки y = uv , где u и v - две неизвестные функции, исходное уравнение преобразуется к виду

u′v + vu ′ + P(x)uv = Q(x) , или u[v′ + P(x)v] + uv ′ = Q(x)

Пользуясь тем, что одна из неизвестных функций (например,v ) может быть выбрана совершенно произвольно (поскольку лишь произведение uv должно удовлетворять исходному уравнению), за v

принимают любое частное решение уравнения v′ + P(x)v = 0 (например, 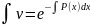) обращающее, следовательно, в нуль коэффициент при u в последнем уравнении. Тогда предыдущее уравнение примет вид: vu′ = Q(x) или

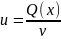
т. е.

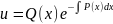
откуда:

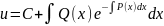
Общее решение исходного уравнения находится умножением u на v

[ ]