Лекция 1.

Числовые ряды.

Основные сведения о рядах.

1. Числовым рядом называется бесконечная последовательность чисел, соединенных знаком сложения

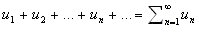
Числа u₁, u_2…,называются числами ряда, член u_n- -общим или n-м членом ряда, сумма n первых членов ряда u₁ + u₂ + u₃ + … + u_n + … = S, или  = S. называется n-й частичной суммой ряда.

2. Ряд называется сходящимся , если существует конечный предел последовательности его частичных сумм, то есть

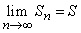
Число S называется суммой ряда, если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

3. Отбрасывание или переписывание к ряду конечного числа членов не влияет на сходимость или расходимость ряда.

Примеры:

1. Покажем, что ряд:

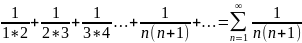сходится.

Возьмем сумму n- членов ряда.

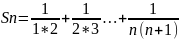
Слагаемые этой суммы могут быть представлены в виде:

, ,

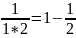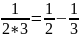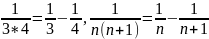
Поэтому,

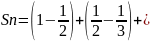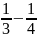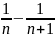( ) +…+( )=1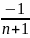

Отсюда следует, что предел последовательности частичных сумм данного ряда равен 1.

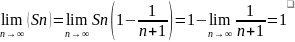
Таким образом, ряд сходится, и его сумма S равна 1.

2. Установим, сходится или расходится ряд:

1-1+1-1+….+ +…=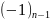

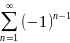
Последовательность его частичных сумм имеет вид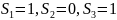 , 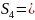0 и значит, не расходится ни к какому пределу, поэтому данный ряд расходится.

3. Рассмотрим ряд, составленный из элементов геометрической прогрессии.

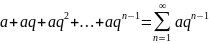
Числовая сумма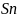 этого ряда при q≠1 имеет вид

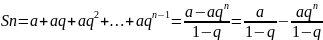
Отсюда,

1)Если |q|<1, то 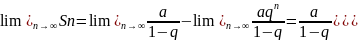, т.е ряд сходится и его сумма S=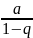

Например, при а=1,q=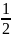

S=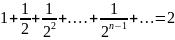

2) Если |q|>1, то 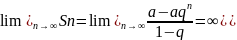, т.е. ряд расходится.

3) При q=1 ряд принимает вид а+а+а+…+а+…

В этом случае 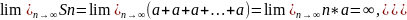т.е. ряд расходится.

4) При q=-1 ряд принимает вид а-а+а-а+…, т.е.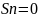 , при n-четном и 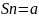, при n-нечетном. Следовательно, 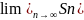не существует и ряд n .

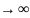Таким образом, ряд является сходящимся при |q|≤1 и расходящимся при Если |q|≥1

Необходимое условие сходимости ряда:

Если ряд 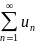сходится, то предел его общего члена при n равен нулю

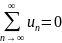
При нарушении необходимого условия сходимости ряда, т.е. если предел общего члена ряда при n не существует или если он не равен 0, ряд расходится.

Заметим, что если предел общего члена ряда равен 0, то вывод о сходимости или расходимости ряда можно сделать только после дополнительного исследования.

Гармонический ряд

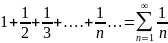
Этот ряд расходится.

Обобщенный гармонический ряд

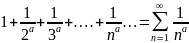
Где а- некоторое число.

Этот ряд сходится, если а>1 ,

расходится, если а≤1

Пример:

Числовой ряд

3+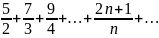 является расходящимся, если его общий член 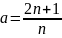не стремиться к нулю.

Лекция 2. Признаки сходимости числовых рядов с положительными членами.

Пусть имеется 2 числовых ряда с положительными членами:

а₁ + а₂ + а₃ + … + а_n + …;(1)

в₁ + в₂ + в₃ + … + в_n + … (2)

где а_n >0, в_n >0, для всех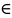 n N

для таких рядов справедливы следующие признаки сходимости.

Признак сравнения:

Пусть общие члены рядов (1) и (2) (с положительными членами)связаны неравенства а_n ≤ в_n для всех n N.

Тогда:

1. Если ряд (1) сходится, то сходится и ряд (2);

2. Если ряд (2) расходится, то расходится и ряд (1).

При применении признака сравнения обычно в качестве эталонных рядов рассматривают следующие ряды:

1. Сумма членов геометрической прогрессии

2. Гармонический ряд

3. Обобщенный геометрический ряд.

Примеры:

1. Числовой ряд

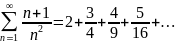
Является расходящимся, так как его общий член в_n 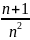больше общего члена а_n

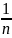
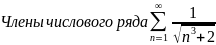• положительны.

Имеем:

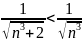
Поскольку ряд 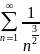сходится, то по признаку сравнения сходится исходный ряд.

Признак Даламбера:

Пусть для числового 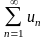с положительными члены предел отношений последующего члена к предыдущему равен 2.

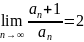
1. Если 2<1, ряд сходится

2. Если 2>1, ряд расходится

3. Если 2=1, ряд может сходится, и расходиться.

=

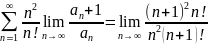2. Числовой ряд

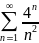расходится, для него

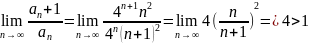
По признаку Даламбера ряд расходится.

3. Для числового ряда

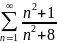имеем:

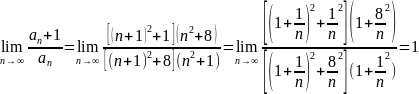
Признак Даламбера не позволяет выяснить вопрос о сходимости ряда.

Однако этот ряд является расходящимся по необходимому признаку,

т.к.

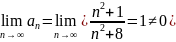
Предельный признак сравнения:

Пусть 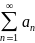и 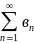- ряды с положительными членами и существует конечный предел отношения их общих членов.

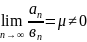
Тогда ряды одновременно сходятся и расходятся.

Пример:

Для числовых рядов

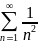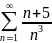и предел отношения общих членов равен 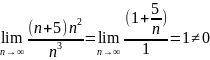Поскольку первый ряд, как обобщенный гармонический , сходится, то по предельному признаку сравнения сходится и второй ряд.

Интегральный признак сходимости:

Пусть все члены числового ряда положительны и не возрастают

а₁≥ а₂≥ …≥а_{n …}

Пусть существует непрерывная невозрастающая функция y= f (x). Определенная при всех х≥1 такая, что F(1)= а₁, f(2)= а_2, f(n)= а_n

Тогда для сходимости числового ряда необходимо и достаточно, чтобы сходился несобственный интеграл

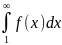
Пример:

Для а>1 члены обобщенного гармонического ряда 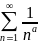положительны и не возрастают. Рассмотрим функцию f(х)= ( ).

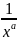Для х≥1 эта функция непрерывна и не возрастает, кроме того F(n)=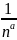 , т.е. для нее выполнены все условия интегрального признака сходимости.

Несобственный интеграл 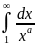является сходящимся при а>1. Действительно неопределенно сходимости несобственного интеграла имеем:

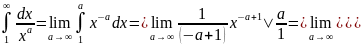
Поэтому обобщенный гармонический ряд при а>1 является сходящимся.