9. Определение высоты стационарного спутника.

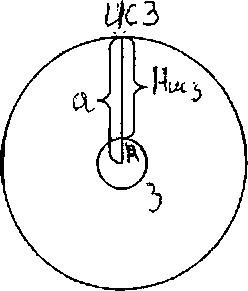
В зависимости от J спутники делятся на:

J=90˚ - полюсные

J=0˚ -экваториальные

0˚<J<90˚ - наклонные

Стационарным называется спутник, который постоянно находится над одной и той же точкой Земли. Это возможно если орбита спутника расположена в плоскости экватора и период обращения спутника равен периоду обращения Земли вокруг своей оси.

H – высота ИСЗ над поверхностью Земли;

а – большая полуось орбиты ИСЗ;

R=6378.211 км;

Т – период обращения ИСЗ;

Μ = 3,9806∙10⁵ км³/с²

км

H_исз=a-R=42221.996-6378.211=35843.785 км

10. Вычисление некоторых параметров исз.

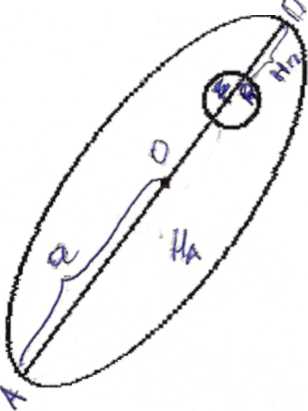
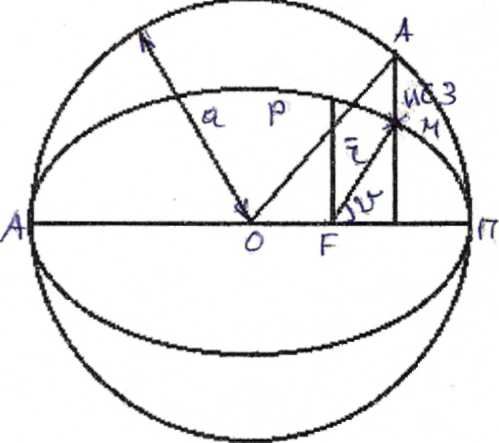
H_П – высота перигея; E – эксцентрическая аномалия;

H_A – высота апогея; -радиус-вектор ИСЗ;

АП – линия апсид; P – фокальный параметр;

-истинная аномалия; R=6378211м, радиус Земли

а – большая полуось орбиты;

М – средняя аномалия (дуга окружности)

Н_А= 1068500м

Н_п= 251750м

Дано:

=32˚

Е=43˚

Вычисления:

1. Большая полуось орбиты спутника

м

2. Эксцентриситет орбиты ИСЗ

3. Фокальный параметр

P=a∙(1-e²)= 7015644,825м

4. Радиус-вектор ИСЗ

м

м

5. Скорость ИСЗ в перигее:

км/с

6. Скорость ИСЗ в апогее

км/с

7. Средняя аномалия

M=E-e∙sinE=40˚43΄58.54˝

8. Период обращения

11. Определение параметров орбиты космического корабля движущегося по орбите вокруг Солнца.

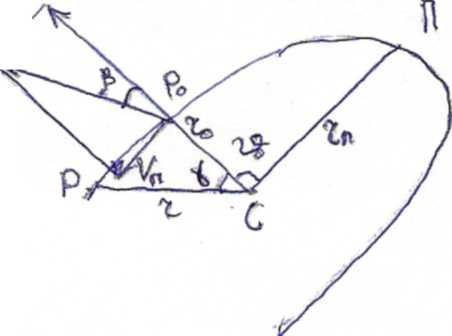
Космический корабль совершает перелет с выключенным двигателем в межпланетном пространстве. Расстояния от планет таковы, что их притяжением можно пренебречь и учитывать только силу солнечного тяготения.

В начальный момент времени t₀, когда корабль находился в P₀ на гелиоцентрическом расстоянии r₀=1.5∙10¹¹м, он имел гелиоцентрическую скорость V₀=20,5 км/с, причем угол между вектором скорости корабля и его радиус-вектором в этот момент был равен β=50˚15΄.

Найти:

1.Истинную аномалию корабля в начальный момент времени t₀;

2.Гелиоцентрическое расстояние r_n в момент прохождения через перигей;

3.Эксцентриситет е и фокальный параметр P орбиты корабля.

Решение:

Пусть k=1,32718∙10²⁰м³/с² – гравитационный параметр Солнца.

В момент t₀ найдем:

где

откуда

Из уравнения орбиты космического корабля получим:

С учетом этого найдем:

1. 2. ;

3.

4.

12. Определение начальной скорости и ориентирующего угла для перехода спутника с одной орбиты на другую.

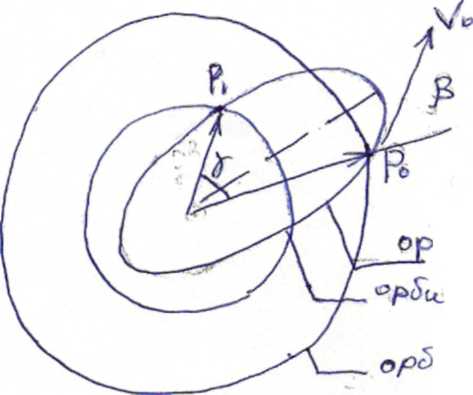
ИСЗ находится в точке Р₀ на орбите Земли (R_ор Земли =1,48∙10⁸ км), он должен совершить перелет к орбите Венеры и пройти через заданную точку Р₁ орбиты Венеры (R_ор Венеры = 1,08∙10⁸ км)

Определить каким должен быть угол β и V_0min, если γ=47˚10΄

Решение:

1. Модуль скорости материальной точки. Движущейся по кеплеровой орбите

где fM=1.32718∙10¹¹ км³/с²

P=a(1-e²) – фокальный параметр

2. Выполним преобразование этой формулы с использованием

а) интеграла энергии

б) интеграла площадей

в) интеграла орбиты

3. Тогда получим следующую формулу

км/с

где

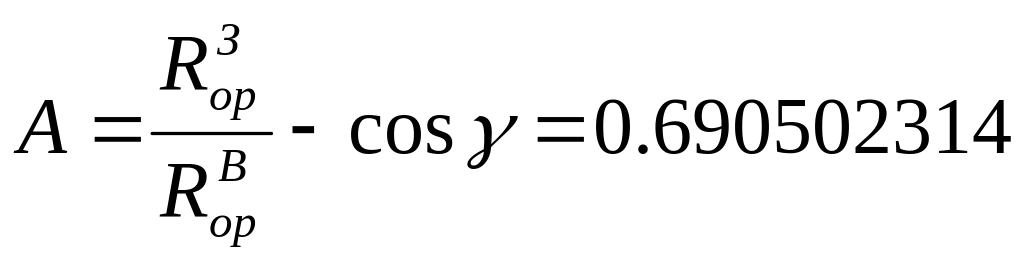
B=sin γ=0.734322509