17.Общая схема межотр. Б-са, осн.Бал.Соотн.Мат.М-ль моб.Реш.С-мы ур-й моб

В основу моделей МОБ положены следующие предположения:

1. Нац. экономика страны производит только 1 вид продукции.

2. Каждая отрасль потребляет продукцию других отраслей, причем если производство продукции некоторой отрасли увеличили в k раз, то и объемы потребления в этой отрасли также увеличатся в k раз.

3.Часть выпускаемой продукции используется в сфере материального производства и сфере услуг, 2-я часть идет на гос. потребление ДХ и ВН.

В основу моделей положен МОБ – таблица, которая характеризует производство и распределение валовой продукции, а также описывает элементы валовой стоимости.

∑Xij+Yi=Xi

∑ Xij+Vj=Xj

∑Xi=∑Xj

∑Yi=∑Vj

∑Vj=V1j+V2j+V3j+V4j-V5j

Aij=Xij/Xj

∑∑∑

x=(E-A)^-1Y – формула для расчеты ВВ

18.Коэф.Полн.И косв.Затрат.Коэф.Полн.З-т ф-в пр-ва.Модель моб с уч.Ф-в пр-ва

Определение 1. Числа a_ij = X ij / Xj называются коэффициентами прямых затрат.

Их экономический смысл состоит в том, что они представляют собой долю

продукции i-й отрасли в затратах на производство единицы (одного рубля)

продукции j-й отрасли.

19.Построение с-мы цен на осн.Моб

20.Оптимизац.Модели на основе моб

Простейшая оптимизационная модель межотраслевого баланса:

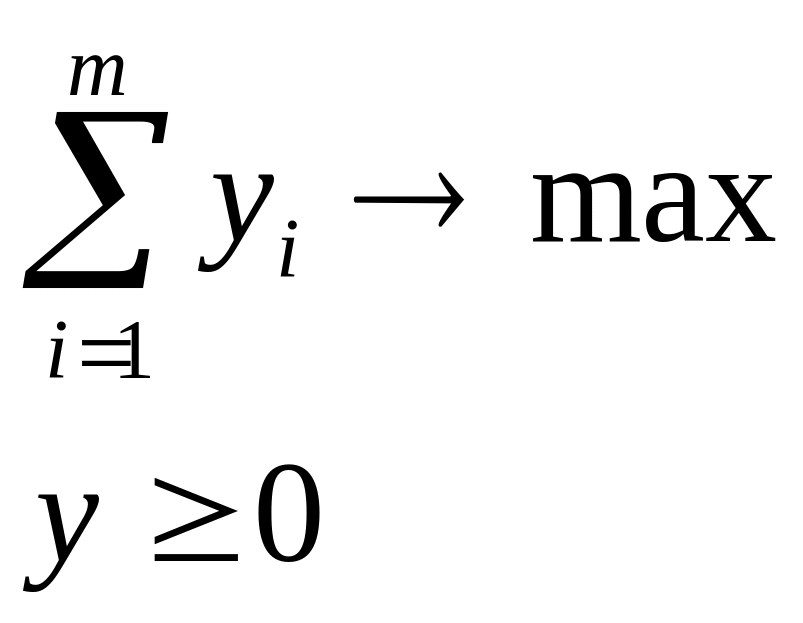
m – число отраслей, y_i – конечное использование i-той отрасли.

Цель – получение максимального ВВП со стороны спроса.

Целевая функция в векторном виде: (Е; у)→ max, где Е – m-мерный единичный вектор (1;1;m;1).

На практике в оптимальном плане для некоторых отраслей конечное использование = 0. Для вектора конечного использования необходимо задать верхнюю и нижнюю границу:

d_-≤y≤d₊ , где d_- и d₊ - векторы, задающие нижнюю и верхнюю границу.

Вместо условия можно задавать строгие сдвиги в экономике:

где - вектор валового выпуска в i-той отрасли

– ВВ i-той отрасли за предыдущий год

α - темп перестройки отрасли.

Рассмотрим равенство . Т.к. 1й игрок максимизирует V, то он одновременно минимизирует при ограничениях , .

Рассмотрим равенство . Т.к. 2й игрок стремится к минимизации V, то он максимизирует . Таким образом, .

Таким образом, нужно решить две оплтимизационные задачи линейного программирования. Из теории двойтвенности вытекает, что эти задачи разрешимы. Их можно решить симплекс-методом.

Допустим, если решили первую задачу и получили оптим. план x^* = (x₁^*, x₂^*,…, x_m^*).

Тогда решаем 2ую задачу и получаем y^* = (y₁^*, y₂^*,…y_n^*)

Затем вычисляем цену . Оптимальная смешанная стратегия:

Это есть основная теорема матричной теории выбора