
- •2.Необход и дост условие..:
- •25.Дифференциальные уравнения первого порядка с разделяющимися переменными.
- •26.Линейные дифференциальные уравнения первого порядка.
- •27. Дифференциальные уравнения второго порядка.
- •28.Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •1.Структура общего рещения ур-ия(1)
- •29. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •30.Понятие числового ряда и суммы ряда. Геометрическая прогрессия.
- •33. Признак сравнения для положительных рядов. Признак Даламбера и Коши.
- •38.Ряды Тейлора и Маклорена.
1. Основные
теоремы дифференциального исчисления.
Т Ролля.
Пусть на [ ]
определена ф-цияf(x),
причём: 1) f(x)
непрерывна на [
]
определена ф-цияf(x),
причём: 1) f(x)
непрерывна на [ ];
2)f(x)
дифференцируема на (
];
2)f(x)
дифференцируема на ( );
3)f(
);
3)f( )
=f(
)
=f( ).
Тогда существует т.
).
Тогда существует т. (
(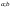 ),
в которойf
(
),
в которойf
( )
= 0.Т Лагранжа.
Пусть на
отрезке [
)
= 0.Т Лагранжа.
Пусть на
отрезке [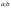 ]
определена ф-цияf(x),
причём 1) f(x)
непрерывна на [
]
определена ф-цияf(x),
причём 1) f(x)
непрерывна на [ ];
2)f(x)
дифференцируема на (
];
2)f(x)
дифференцируема на (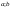 ).
Тогда сущ-ет т.
).
Тогда сущ-ет т. (
(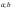 )
такая, что справедлива ф-ла
)
такая, что справедлива ф-ла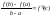 .Рав-во
.Рав-во
f( )−f(
)−f( )=f
'(
)=f
'( )(
)( )
наз-сяформулой
Лагранжа или
формулой
конечных приращений.
Т Коши. Пусть
ф-ции f(x)
и g(x)
непрерывны на [
)
наз-сяформулой
Лагранжа или
формулой
конечных приращений.
Т Коши. Пусть
ф-ции f(x)
и g(x)
непрерывны на [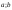 ]идифференцируемы
на (
]идифференцируемы
на (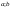 ).
Пусть, кроме того,g'(x)≠0.
Тогда на
).
Пусть, кроме того,g'(x)≠0.
Тогда на
(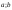 )
существует т.
)
существует т. такая, что справедлива ф-ла
такая, что справедлива ф-ла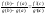 Ф-ла (*) наз-сяформулой
Коши или
обобщённой
формулой конечных приращений.
Ф-ла (*) наз-сяформулой
Коши или
обобщённой
формулой конечных приращений.
2.Необход и дост условие..:
пусть f=(x) опре-на на множе-ве Х и внутри его им. конеч. произ-ю,на концах сохран. непрерыв-ть,если концы прин. мно-ву Х.Чтобы f(x) б. постоя-й на мно-ве Х необ-мо и дост-но,чтоб выпол-сь раве-во f``(x)=0 внутри мно-ва Х. След-е из т-мы:пусть f(x) и g(x) опре-ны на мно-ве Х и внутри его сущ. Конеч. произ-е f``(x),g`(x).Тогда,если f``(x)=g`(x),х прин. Х,то f``(x)=g`(x)+с. Т-ма(усл моно-ти ф-и):пусть y=f(x) опре-на на мно-ве Х и внутри им. конеч. f``(x). Для того,чтоб y=f(x) б. моното-о возрас-й (убыв-й) надо,чтоб f``(x)>0 (f``(x)<0)/.
3.Достат. условия экстре-ма ф-и: Максимум и минимум ф-ции называют экстремумом. Значение аргумента, при кот достигается экстремум, наз-ся точкой экстремума.Необход усл экст-ма:y=f(x) опр-на на инт-ле (а,в) и им конеч прои-ю,тогда,чтоб ф-я в т х0 прин (а,в) достигала экст-ма,нео-мо выполн рав-ва f``(x0)=0. Точки,в кот прои-я=0-стационарные, критич,,подозрит на экстре-м. Стационарные т-ки, а также т-ки, в которых ф-ция имеет бесконечную производную или в кот производная не сущ-ет, наз-ся критическими. Т-ма(1-е дост усл-е):пусть хо-критич т 1-го рода. Предполож,что f(x) диф-ма в некот окре-ти т. хо(хо- δ ;х0+ δ) и f``(x) сохран свой знак слева и справа от т хо.Тогда:1.если при перех-е слева направо ч-з т х0 произ-я мен с + на -,то в т х0 y=f(x) им max;2. если при перех-е слева направо ч-з т х0 произ-я мен с – на +,то ф-я в т х0 им min;3.если прои-я знака не мен,то т х0 не явл т экстремума.
Т-ма(2-е дост усл):пусть х0 стацио-я точка,в кот f(x) дважды дифф-ма.Тогда:1.если f```(x0))<0,то х0-т max;2.f```(xo)>0,то х0-т min.
Замеча-е:2-м дост усл нельзя поль-ся,есди 2-я произ-я в т х0 обращ в 0 или не сущ. В так случае исп 1-е дост усл.
4.Выпук-ть и
вог-ть: Кривая
y=f(x)
наз выпу-й
на инт-ле (а,в),если все точки кривой леж
ниже люб её касате-й на это инт-ле: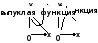
Кривая
y=f(x)
вогнут на ин-ле (а,в),если все т кривой леж выше люб её касат-й на этом инт-ле. Точки,в кот выпу-ть смен на вог-ть и наоборот-т перегиба. Т-ма1(дост усл вы-ти,аог-ти):Пусть y=f(x) 2-ды диф-ма га ин-ле (а,в).Тогда:1.если на ин-ле (а,в) f```(x)>0,то на нём ф-я вог-я; 2.еслина ин-ле (а,в) f```(x)<0,то на нём ф-я вып-я. След-е:точки перегиба надо иск среди точек,где 2-я произ-я=0 или не сущ.Такие т наз критич т 2-го рода.Но не всяк критич т 2-го рода=т перегиба. Т-ма2(дост усл пере-а):Пусть х0-критич т 2-го рода.Если при перех-е ч-з т х0 2-я произ-я мен знак,то т х0 явл т перегиба y=f(x).
№5.Асимптоты..:
Асимптотой
графика функции

 называется прямая , к которой стремится
график функции, когда точка вдоль по
графику стремится в бесконечность.
Т-ма2:Если
называется прямая , к которой стремится
график функции, когда точка вдоль по
графику стремится в бесконечность.
Т-ма2:Если
 или
или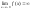 ,
то прямая
,
то прямая будетвертикальной
асимптотой графика
функции
будетвертикальной
асимптотой графика
функции
 .Т-ма3:Если
существуют конечные пределы
.Т-ма3:Если
существуют конечные пределы
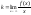 и
и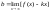 , то прямая
, то прямая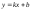 будетнаклонной
асимптотой
графика функции
будетнаклонной
асимптотой
графика функции
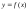 .
.
Следует иметь в
виду, что пределы могут быть разные при
 и
и .Т-ма1:
если предел
.Т-ма1:
если предел
 при
х стремя-ся к + беско-ти,т.е.
при
х стремя-ся к + беско-ти,т.е.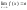 ,то
прямая
y=b-асимптота
кривой y=f(x)
и наз горизонт асим-й.Анал-о при
,то
прямая
y=b-асимптота
кривой y=f(x)
и наз горизонт асим-й.Анал-о при
 .
.
№6.Нах-е наиб т наим зн-я:Если наиб и наим зн-я ф-я приним внутри отре-ка,то это зн-е-min,max. 1. Находим критические точки первой производной и выбираем из них те, которые лежат в рассматриваемом интервале (a;b).
2. Вычисляем значения функции в найденных критических точках и на концах интервала в точках a и b.3. Выбираем из полученных значений наибольшее и наименьшее. В случае произвол проме-ка Х верна т-ма:пусть y=f(x) непре-на на произвол проме-ке \Х и им на нём лишт один экст-м. Тогда:1.если экст-м явл max-м,то и наиб зна-ем ф-и; 2.если экстре-м явл min,то это и наим зн-е ф-и.
№7.Понятие ф-и неск пере-х:Люб пару чисел м изобр на плос-ти точкой,т.е. это некот мно-во точек пло-ти.Рассмотр некот мно-во Z дей-й чисел.Опр:если кажд паре дейст-х чисел (x,y) € D соот-т одно определ дей-е число z€Z,то говор,что на мно-ве D задана z=f(x,y) со зна-ми во мно-ве Z.
z=f(x,y)-ф-я
переме-х,а перем-е x,y-независим
переме-е или аогме-ы. Множество D
наз обл определения ф-и.Обл опр ф-и по
переме-м x,y-мно-во
точек плоскости.Ф-ю 2-х пере-х м задав
анали-ки,граф-ми и таб-ми способами.
Опр. Число
![]() называетсяпределом
ф-и
f(x,y)
в т с коор-ми (x0,y0),
если для люб посл-ти точек ((xn,yn))
,стре-ся к т с коор-ми (x0,y0),коо-ты
кот отличны от т (x0,y0),коо-ты
кот отл-ны от т (x0,y0)
и не выход из обл опр-я ф-и.Соотве-я
послед-ть знач-й ф-и (f(xn,yn))
называетсяпределом
ф-и
f(x,y)
в т с коор-ми (x0,y0),
если для люб посл-ти точек ((xn,yn))
,стре-ся к т с коор-ми (x0,y0),коо-ты
кот отличны от т (x0,y0),коо-ты
кот отл-ны от т (x0,y0)
и не выход из обл опр-я ф-и.Соотве-я
послед-ть знач-й ф-и (f(xn,yn))
![]() A.
A.
![]() .(в
пре-ле снизу надо доп для y).Заме-е:все
т-мы о пред-х для 1-й перем-й пре-ся на
случай ф-и 2-х пере-х.Опр: z=f(x,y)-непре-я
в т с коор-ми (x0,y0),если
в ней сущ предел и он=зга-ю ф-и в эт точке
.(в
пре-ле снизу надо доп для y).Заме-е:все
т-мы о пред-х для 1-й перем-й пре-ся на
случай ф-и 2-х пере-х.Опр: z=f(x,y)-непре-я
в т с коор-ми (x0,y0),если
в ней сущ предел и он=зга-ю ф-и в эт точке
![]()
(в пределе снизу для y)
№8.Частн-е
произ-е..:Пусть z=f(x,)
опре-на в некот обл D.Рассмотр
произвол т (x,y)
€ D.Придадим
приращение аргу-ту x
 ,
оставляя переменную
,
оставляя переменную без
изменения, тогда функция получит частое
приращение
без
изменения, тогда функция получит частое
приращение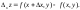 Рассмотр
отн-е
Рассмотр
отн-е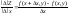 (1)
(1)
Опр:если сущ
предел отн-я (1) при
 →0,то
этот предел-частная произв-я по х ф-иf(x,y)в
т с коор-ми (x,y)
и обозн-ся
→0,то
этот предел-частная произв-я по х ф-иf(x,y)в
т с коор-ми (x,y)
и обозн-ся
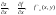 .Т.о.f`x(x,y)=
.Т.о.f`x(x,y)=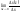 =
= .
Также опред произ-я по ф-иf(x,y)
в т (x,y)
и обозн
.
Также опред произ-я по ф-иf(x,y)
в т (x,y)
и обозн
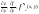 Т.о.f`y(x,y)
=
Т.о.f`y(x,y)
=
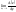 =
= .
Заме-е:из опр час-й прои-й по х следует,что
част прои-ю по х м рассматр как обыкнвен
произ-ю ф-и одной переем-й х,а пере-ю у
счит постоян величиной и наоборот.Пустьz=f(x,y)
им непрерыв част произ-е по х и у в некот
обл D.Рассмотр
т.(х,у)€D.
Аргумен-м х и у прид прира-е ∆х и ∆у,тогда
ф-я z
получ прира-е ∆z.
.
Заме-е:из опр час-й прои-й по х следует,что
част прои-ю по х м рассматр как обыкнвен
произ-ю ф-и одной переем-й х,а пере-ю у
счит постоян величиной и наоборот.Пустьz=f(x,y)
им непрерыв част произ-е по х и у в некот
обл D.Рассмотр
т.(х,у)€D.
Аргумен-м х и у прид прира-е ∆х и ∆у,тогда
ф-я z
получ прира-е ∆z.
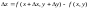 .М
док,что в эт случае полн прир-е ∆z
в придставим виде: (1)
.М
док,что в эт случае полн прир-е ∆z
в придставим виде: (1)
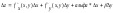 ,где
альфа иβ-бес-но малые величины при
∆x→0,∆y→0.
,где
альфа иβ-бес-но малые величины при
∆x→0,∆y→0.
Опр:полн диф-м
z=f(x,y)-выражение:
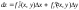 (2).Полн
диф-л-сумма частн диф-в по х и у.Приращ-е
аргу-в ∆х и ∆у наз диф-ми независимых
переем-х и обозн ч-зdx,dy.Тогда
ф(2):
(2).Полн
диф-л-сумма частн диф-в по х и у.Приращ-е
аргу-в ∆х и ∆у наз диф-ми независимых
переем-х и обозн ч-зdx,dy.Тогда
ф(2):
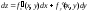 .При
ДОС-но мал вели-х ∆х и ∆у в раве-ве (1)
з-м и 4-м сла-м принебе-м в ре-те получ
раве-во: ∆z≈dz.
f(x+∆x,y+∆t)≈f(x,y)+f`x(x,y)∆x+f`y(x,y)∆y-для
приближ вычи-й.
.При
ДОС-но мал вели-х ∆х и ∆у в раве-ве (1)
з-м и 4-м сла-м принебе-м в ре-те получ
раве-во: ∆z≈dz.
f(x+∆x,y+∆t)≈f(x,y)+f`x(x,y)∆x+f`y(x,y)∆y-для
приближ вычи-й.
№9.Экстрем-м ф-и неск пере-х…:Опр:точка с коор-ми (х0,у0)- точка max (min),если сущ такая δ-окре-ть эт точки,что для всех т с коо-ми (х,у),взятых из окр-ти т с коор-ми (х0,у0),кроме т с коор-ми (х0,у0),выполн раве-во f(x,y)<f(x0,y0)-max (f(x,y)>f(x0,y0))-min.Т-ма(необх усл экст-а):если т с коор-ми (х0,у0)-т экст-ма z=f(x,y) и в ней сущ обе част произ-е,но они в т с коо-ми (х0,у0)=0. Док-во:рассмотр ф-ю 2-х переме-х z=f(x,y),Зафиксир зн-е переме-й у,положим у=у0.Тогда ф-я 2-х пере-х превра-ся в ф-ю 1-й пере-й,т.е. z=f(x,y0).По данному,z=f(x,y) в т с коор-ми (х0,у0) им экст-м,тогда z=f(x,y0) в т x=x0 также им экст-м.Используя необх усл экст-ма получ f`x(x0,y0)=0.Также док-ся 2-е рав-во.Точки,в кот все част прои-е=0,наз крити-и,стационар точками.В кртич точках невсегда б экст-м.Рав-во о част-х произ-х-необход усл,но недоста-е.
№10Понятие об эмпирических формулах и методе наименьших квадратов.б) Подбор параметров линейной ф-ции. Выравнивание по прямой, параболе.В естествознании, технике и экономике часто приходится иметь дело с эмпирическими формулами, т.е. формулами, составленными на основе обработки статистических данных или результатов опытов. Одним из распространенных приемов построения таких формул является метод наименьших квадратов. Изложим идею этого способа, ограничиваясь случаями линейной и квадратичной зависимости. Пусть требуется установить зависимость между двумя величинами x и y, например, между стоимостью потребляемого сырья и стоимостью выпущенной продукции. Произведем обследование n видов продукции и представим результаты исследования в виде таблицы:
|
x |
x1 |
x2 |
... |
xn |
|
y |
y1 |
y2 |
... |
yn |
Из анализа таблицы нелегко обнаружить наличие и характер зависимости между x и y. Поэтому обратимся к графику. Допустим, что точки, взятые из таблицы (опытные точки) группируются около некоторой прямой линии. Тогда можно предположить,что между x иy существует линейная зависимостьy= ax+b, где a и b - коэффициенты, подлежащие определению,y - теоретическое значение ординаты. Проведя прямую “на глаз”, можно графически найти b и a=tg , однако это будут весьма неточные результаты. Для нахождения a, b применяют метод наименьших квадратов. Отыскание уравнения прямой по эмпирическим данным называется выравниванием по прямой, а отыскание уравнения параболы -выравниванием по параболе.
№11. Пусть ф-ция f(x) определена на X. Ф-ция F(x) – первообразная для f(x) на X, если F’(x)=f(x) для любого x € X.
F(x) – первообразная, F(x)+C – первообразная.

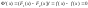 для
для

 ;
;
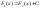
Совокупность всех первообразных F(x)+C для ф-ции f(x), определенное на X, называется неопределенным интегралом от ф-ции f(x) на X и обозначается

 ;
;

Основные свойства неопределенного интеграла.
1).
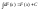
2).
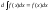

3).
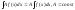
4).

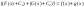
Таблица основных интегралов:
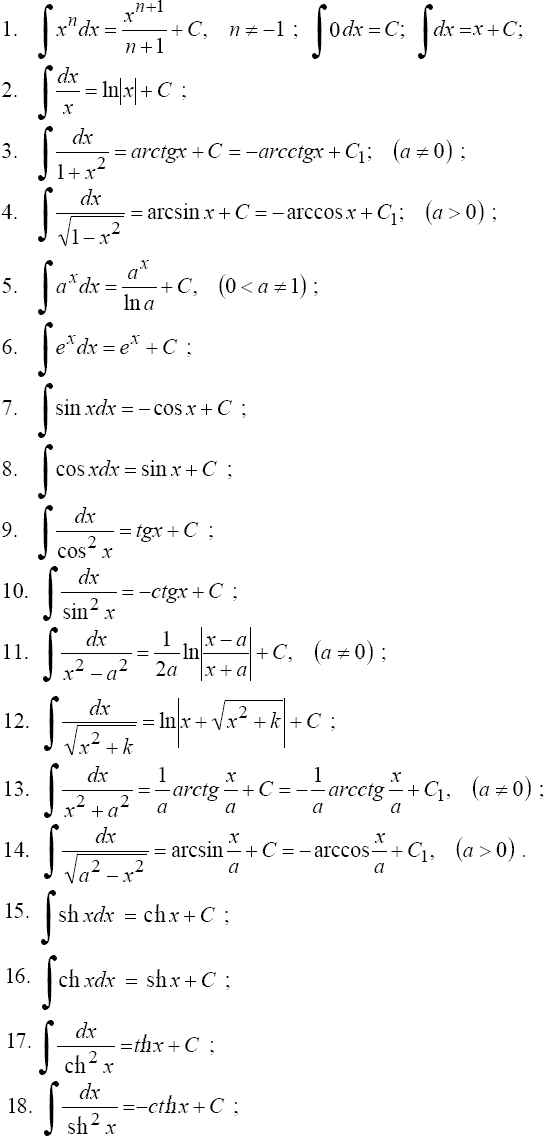
№12
Теорема:
Пусть определена
и диф-ма наX.
U-
множество значений ф-ции
определена
и диф-ма наX.
U-
множество значений ф-ции
 .
Дляf(U)
существует F(U)
на U.
.
Дляf(U)
существует F(U)
на U.
 Тогда дляg(x)
на X
сущ-т первообразная
Тогда дляg(x)
на X
сущ-т первообразная
 ,
т.е.
,
т.е.
Док-во:

На практике:

. Интегрирование по частям: теор: Пусть каждая из функций u(x) и v(x) дифференцируема на интервале {x} и пусть, кроме того, на этом интервале существует первообразная для функции v(x)u'(x). Тогда на интервале {x} существует первообразная для функции uv' и справедлива формула u(x)v'(x)dx=u(x)v(x)– v(x)u'(x)dx. => udv=uv–vdu - формула интегр. по частям. Док: Запишем формулу для дифференцирования произведения двух функций (u(x)v(x))'=u'(x)v(x)+u(x)v'(x). Интеграл от производной (u(x)v(x))' существует по определению: (u(x)v(x))'dx=u(x)v(x)+c. Интеграл u'(x)v(x)dx существует по условию теоремы. => по линейному свойству интеграла существует интеграл от функции u(x)v'(x)=(u(x)v(x))'–u'(x)v(x) и u(x)v'(x)dx=(uv')dx–u'v(x)dx=u(x)v(x)–u'v(x)dx. Теор. док.
№ 13,14Правильная рациональная дробь раскладывается на сумму элементарных дробей.
Типы дробей:
1)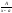 ,
2)
,
2)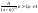 ,
3)
,
3) ,4)
,4) 1)
1) 2)
2)


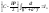 - рекуррентная формула. Вывод: интеграл
от любой рациональной ф-ции выражается
элементарной ф-циейln,arctg,
степенная.
- рекуррентная формула. Вывод: интеграл
от любой рациональной ф-ции выражается
элементарной ф-циейln,arctg,
степенная.
№15. Интегралы
вида ![]() рационализируются
подстановкой
рационализируются
подстановкой![]() ,
где
,
где![]() -
общий знаменатель дробей
-
общий знаменатель дробей![]() .
2.
Интеграл от дифференциального
бинома
.
2.
Интеграл от дифференциального
бинома![]() выражается
через конечную комбинацию элементарных
функций лишь в трех случаях:
2.1.
выражается
через конечную комбинацию элементарных
функций лишь в трех случаях:
2.1.![]() -
целое число, подстановка
-
целое число, подстановка![]() (
(![]() -
наименьший общий знаменатель дробей
-
наименьший общий знаменатель дробей![]() ).
2.2.
).
2.2.![]() -
целое число, подстановка
-
целое число, подстановка![]() (
(![]() -
знаменатель дроби
-
знаменатель дроби![]() ).
2.3.
).
2.3.![]() -
целое число, подстановка
-
целое число, подстановка![]() (
(![]() -
знаменатель дроби
-
знаменатель дроби![]() ).В
остальных случаях интеграл от
дифференциального бинома не выражается
через конечное число элементарных
функций.
3.
Интеграл вида
).В
остальных случаях интеграл от
дифференциального бинома не выражается
через конечное число элементарных
функций.
3.
Интеграл вида ![]() ,
подстановка
,
подстановка![]() .
4.
Интеграл вида
.
4.
Интеграл вида![]() ,
подстановка
,
подстановка![]() или
или![]() .
5.
Интеграл вида
.
5.
Интеграл вида![]() ,
подстановка
,
подстановка![]() или
или![]() .
6.
Интеграл вида
.
6.
Интеграл вида![]() с
помощью подстановки
с
помощью подстановки![]() сводится
к одному из интегралов (3) – (5).
7.
Интеграл вида
сводится
к одному из интегралов (3) – (5).
7.
Интеграл вида![]() можно
также упростить подстановками Эйлера:
7.1. Если
можно
также упростить подстановками Эйлера:
7.1. Если![]() 7.2. Если
7.2. Если![]() 7.3. Если трехчлен
7.3. Если трехчлен![]() имеет
различные корни
имеет
различные корни![]() ,
то
,
то![]()
№16. Интегрирование выражений, содержащих тригонометрические функции.
Рассмотрим интеграл вида
1)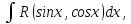 R
– некоторая рациональная ф-я. Находится
с помощью универсальной подстановки
tg
R
– некоторая рациональная ф-я. Находится
с помощью универсальной подстановки
tg Убедимся в этом: x/2=arctgt
Убедимся в этом: x/2=arctgt
X=2arctgt
Dx=2dt/(1+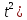 Sinx=2sin(x/2)cos(x/2)=2tg(x/2)
Sinx=2sin(x/2)cos(x/2)=2tg(x/2)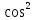 (x/2)=2tg(x/2)/1+
(x/2)=2tg(x/2)/1+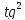 (x/2)
(x/2)
Sinx=2t/(1+
Cosx
=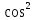 (x/2)-
(x/2)-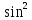 (x/2)=(1-
(x/2)=(1- (x/2))/(1+
(x/2))/(1+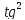 (x/2))
(x/2))
Cosx=(1-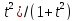
Следовательно
 Замечание:
Интеграл вида:
Замечание:
Интеграл вида:
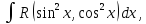 является частным случаем интеграла
(1) и может быть так же вычислен с помощбю
подстановкиtgx/2=t,
но нахождение упростится, если применить
подстановку tgx=t
является частным случаем интеграла
(1) и может быть так же вычислен с помощбю
подстановкиtgx/2=t,
но нахождение упростится, если применить
подстановку tgx=t
X=arctgt,
dx=dt/(1+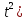
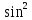 x=
x= x
x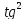 x=
x=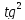 x/(1+
x/(1+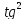 x)
x)
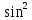 x=
x=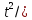 (1+
(1+ )
)
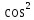 x=1/(1+
x=1/(1+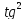 x)
x)
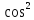 x=1/(1+
x=1/(1+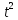 )
)
Т.о.
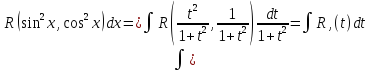 №17.
Геометрическая задача, приводящая к
понятию определённого интеграла.
Определение определённого интеграла.
№17.
Геометрическая задача, приводящая к
понятию определённого интеграла.
Определение определённого интеграла.
Пусть y=f(x) непрерывна и неотрицательна на [a,b].
Рассмотрим фигуру, образованную графиком этой ф-и и прямыми x=a, x=b, y=0.
![]() Эту
фигуру принято называть криволинейной
трапецией. Введём понятие площади
криволинейной трапеции и получим
формулу для её вычисления. Разобьём
отрезок [a,b]
на n
маленьких частей, необязательно разных.
Эту
фигуру принято называть криволинейной
трапецией. Введём понятие площади
криволинейной трапеции и получим
формулу для её вычисления. Разобьём
отрезок [a,b]
на n
маленьких частей, необязательно разных.
A=x0<x1<x2<…<xk-1)<xk<…<xn=b
T[a,b]
Эти точки разбивают [a,b] на n частные отрезки
[xk-1,xk],
k=1
Длины частных отрезков обозначим через ∆xk
На каждом частном
отрезке выберем точку ξk
и вычислим
значение ф-и в этих точках f(ξk)
k=1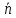
Составим сумму
f(ξ1)
∆x1+
f(ξ2)
∆x2+…+
f(ξn)
∆xn=
Эта сумма представляет собой сумму площадей прямоугольников с высотой f(ξk) и основанием ∆xk
, т.е. площадь ступенчатой фигуры.
Площадь криволинейной трапеции определяется как следующий предел:
S=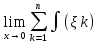 ∆xk
∆xk
Определение определённого интеграла
Рассмотрим ф-ю y=f(x) определённую на [a,b]. Разобьём [a,b] на n произвольных частей.
a=x0<x1<…<xk-1<xk<…<xn=b
Совокупность этих точек назовём разделением Т[a,b]
Длины частных
отрезков обозначим через ∆ xk,
k=1,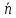 ,
а длину наибольшего λ. На каждом частном
отрезке выберем произвольную точку ξk
и вычислим
значение ф-и f(ξk)
в этих точках.
,
а длину наибольшего λ. На каждом частном
отрезке выберем произвольную точку ξk
и вычислим
значение ф-и f(ξk)
в этих точках.
Сумма δ=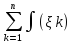 ∆xk
называется
интегральной.
∆xk
называется
интегральной.
Интегральная сумма зависит от разбиения Т[a,b] и от выбора точек ξk.
Введём понятие предела интегральной суммы при λ→0
Рассмотрим какую-либо последовательность Т1,Т2,…,Тn… разбиений отрезка [a,b]
Определение 1.
Последовательность (Тn)
разбиений отрезка[a,b]
называется основной, если соотв.
последовательность (λn)
стремится к 0, т е
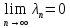
Определение 2. Если для любой основной последовательности (Тn) разбиений отрезка [a,b] соотв. последовательность (δn) интегральных сумм стремится к одному и тому же числу I. Независимо от выбора точек ξk, то это число I называют пределом интегральной суммы при λ→0.
I=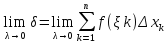
Определение 3
Если существует предел I
интегральной суммы δ при λ→0,
то этот предел называется определённым
интегралом от функции f(x)
на отрезке [a,b]
или в пределах от a
до b
и обозначается I=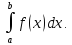
Т. о. по определению

В этом случае функция f(x) называется интегрируемой на [a,b].
№18 Свойства определенного интеграла.
Значение опред. и-ла – это число(любое).
1)Значение опред.
и-ла не зависит от того, какой буквой
обозначена переменная интегрирования,
т. е.
 .
.
 0.
0.
2) В граф.иллюстрации этого случая (a=b) отрезок ab вырождается в точку, а криволин.трапеция вырождается в отрезок, у которого площадь=0
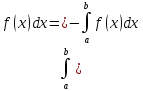
3) Св-во линейности
опред.и-ла.
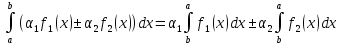 4)Св-во
адитивности опред.и-ла.
4)Св-во
адитивности опред.и-ла.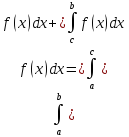 .
Это св-во справедливо для люб.взаимного
расположения точекa,b,c.
.
Это св-во справедливо для люб.взаимного
расположения точекa,b,c.
5)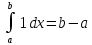
6)Теорема об
интегрировании неравенств: если в
люб.точке x
отрезка ab
выполняется нер-во f(x) g(x),
то ф-ции f(x)
и g(x)
интегрируемы на отрезке ab
и выполняется нер-во:
g(x),
то ф-ции f(x)
и g(x)
интегрируемы на отрезке ab
и выполняется нер-во:
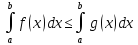
7)Теоремы об оценке
опр.и-ла. 1)Если на отр. ab
ф-ция удовлетворяет нер-ву m f(x)
f(x) M,
то опр. и-л от ф-ции удовл. нер-ву
m(b-a)
M,
то опр. и-л от ф-ции удовл. нер-ву
m(b-a) M(b-a).
2)Если ф-ция y=f(x)
интегрируема на отр. ab,
то
M(b-a).
2)Если ф-ция y=f(x)
интегрируема на отр. ab,
то
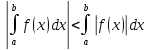
8)Теорема о среднем:
если ф-ция y=f(x)
непрерывна на отр. ab,
то на этом отр. существует т.С, такая,
что
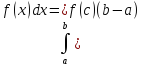 .
.
№19. Теорема о существовании первообразной для непрерывной функции (с доказательством ). Формула Ньютона-Лейбница.
Пусть функция f(x) интегрируема на [a,b]. Тогда, ∀x∈[a,b] каково бы ни было число x из [a,b], функция
f(x) интегрируема и на сегменте [a,x]. Поэтому на интервале (a,b) определена функция F(x)=∫xaf(t)dt, которую называют интегралом с переменным верхним пределом.
Теорема 1 (существование первообразной для непрерывной функции).
Любая непрерывная на интервале (a,b) функция f(x) имеет на этом интервале первообразную. Одной из первообразных является функция
F(x)=∫xaf(t)dt,
Доказательство. Достаточно доказать, что для любого фиксированного x из интервала (a,b)существует предельное значение limΔx→0ΔxF(x+Δx)−F(x), причем это предельное значение равно f(x).
Имеем F(x+Δx)−F(x)=∫x+Δxaf(t)dt−∫xaf(t)dt=∫xaf(t)dt+∫x+Δxxf(t)dt−∫xaf(t)dt=∫x+Δxxf(t)dt.
Формула Ньютона-Лейбница
Связь м/ду понятиями
неопред. и опред.Иустанов.в теореме
Ньютона-Лейбница.Если у=f(х)непрерывна
на конечном отрезке[а;в] иF(х)-некоторая
первообразная для f(х),то
(1):
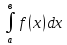 =F(x)│ав=F(в)-F(а).
=F(x)│ав=F(в)-F(а).
1)Док-во базируется на теореме Бароу(И с переменным верхним приделом);2)формула (1) применима только если:а)у=f(х) непрерывна на отр[а;в];б)отр[а;в]конечен;в)для ф-цииf(х)существует первообразная;3)на практике ф-ла (1) релизуется в 3 этапа:а)проверка условий применяемости ф-лы;б)нахождение первообразной при помощи неопред.И от ф-цииf(х);в)подстановка в найденную первообразную вместо перемен.Х границ отр.[а;в],отр.интегрирования.
№20 Теорема: Пусть
f(x)
интегр. на [-a,a],
тогда если f(x)
четная, то
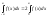 ,
если нечетная, то
,
если нечетная, то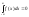 .
.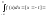
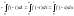
Если f(x) – непрерывная с периодом T, интегрируемая на некотором отрезке длины Т, то она интегрируема на любом отрезке длины Т.

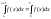
Док-во:
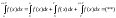
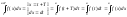
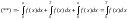
Интегрирование по частям в определенном интеграле.
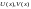 -
непр. диф-е ф-ции на
-
непр. диф-е ф-ции на

 ;
;
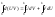 ;
;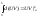 ;
;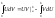
№21 Площадь фигуры

 f(x)-непрерывна
f(x)-непрерывна
x=a,x=b; отр [a,b] оси оХ
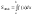

![]()
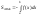
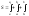
![]()
2)Оббьем тел
вращения![]()
3)Длина дуги кривой.
Пусть известна
функция ![]() и
требуется найти длину дуги, заданной
функцией
и
требуется найти длину дуги, заданной
функцией![]() ,
где
,
где![]() .
.![]()
№22 Несобственные интегралы с бесконечными пределами интегрирования.б)Интеграл Пуассона(без док-ва)
а) Несобственным интегралом с бесконечным верхним переделом ∫+∞а f(x)dx от ф-ии f(x) наз предел интеграла ∫tа f(x)dx, t→+∞, ∫+∞а f(x)dx=limt→+∞ ∫tа f(x)dx. Если этот предел сущ или равен конечному числу, то интеграл наз сходящимся, а противном случае расходящимся. Аналогично: Несобственный интеграл с нижним бесконечным пределом: ∫b-∞ f(x)dx=limt→-∞ ∫bt f(x)dx.
№23
Определение 1. Пусть функция f(x) определена
и неограничена на полуинтервале [а, b),
при этом она ограничена и интегрируема
на любом отрезке [а, с], где а ![]() с
Если существует конечный предел
с
Если существует конечный предел ![]() ,
то он называется несобственным интегралом
функции f(x) на отрезке [а, b] и обозначается
,
то он называется несобственным интегралом
функции f(x) на отрезке [а, b] и обозначается
![]() Аналогичным образом вводится понятие
несобственного интеграла для функции,
неограниченной на полуинтервале (а,
b]:
Аналогичным образом вводится понятие
несобственного интеграла для функции,
неограниченной на полуинтервале (а,
b]:![]() Если
функция неограниченна на интервале
(а, b), и при с этом существуют несобственные
интегралы
Если
функция неограниченна на интервале
(а, b), и при с этом существуют несобственные
интегралы![]() Определение
2. Если несобственный интеграл существует,
то говорят, что интеграл сходится. В
противном случае говорят, что интеграл
расходится.
Теорема 1. Если функция
f(x) непрерывна на полуинтервале [а, b) и
F(x) - произвольная первообразная функции
f(x) на [а, b), тогда
Определение
2. Если несобственный интеграл существует,
то говорят, что интеграл сходится. В
противном случае говорят, что интеграл
расходится.
Теорема 1. Если функция
f(x) непрерывна на полуинтервале [а, b) и
F(x) - произвольная первообразная функции
f(x) на [а, b), тогда![]() Аналогичным
образом находится интеграл от функции,
непрерывной на полуинтервале (а,
b]:
Аналогичным
образом находится интеграл от функции,
непрерывной на полуинтервале (а,
b]:![]() Определение
1. Пусть функция f(x) определена и
неограничена на полуинтервале [а, b),
при этом она ограничена и интегрируема
на любом отрезке [а, с], где а
Определение
1. Пусть функция f(x) определена и
неограничена на полуинтервале [а, b),
при этом она ограничена и интегрируема
на любом отрезке [а, с], где а ![]() с
Если существует конечный предел
с
Если существует конечный предел ![]() ,
то он называется несобственным интегралом
функции f(x) на отрезке [а, b] и
обозначается
,
то он называется несобственным интегралом
функции f(x) на отрезке [а, b] и
обозначается
![]() Аналогичным
образом вводится понятие несобственного
интеграла для функции, неограниченной
на полуинтервале (а, b]:
Аналогичным
образом вводится понятие несобственного
интеграла для функции, неограниченной
на полуинтервале (а, b]:![]() Если
функция неограниченна на интервале
(а, b), и при с этом существуют несобственные
интегралы
Если
функция неограниченна на интервале
(а, b), и при с этом существуют несобственные
интегралы![]() Определение
2. Если несобственный интеграл существует,
то говорят, что интеграл сходится. В
противном случае говорят, что интеграл
расходится.
Теорема 1. Если функция
f(x) непрерывна на полуинтервале [а, b) и
F(x) - произвольная первообразная функции
f(x) на [а, b), тогда
Определение
2. Если несобственный интеграл существует,
то говорят, что интеграл сходится. В
противном случае говорят, что интеграл
расходится.
Теорема 1. Если функция
f(x) непрерывна на полуинтервале [а, b) и
F(x) - произвольная первообразная функции
f(x) на [а, b), тогда![]() Аналогичным
образом находится интеграл от функции,
непрерывной на полуинтервале (а, b]:
Аналогичным
образом находится интеграл от функции,
непрерывной на полуинтервале (а, b]:![]()
№24
Понятие о дифференциальном уравнении.б)Общее и частное решения
а)Дифференциальным уравнением наз уравнение, связывающее искомую ф-цию одной или нескольких переменных, эти переменные и производные различных порядков донной ф-ии.
б)Общим решением дифференциального ур-ния g(x,y,y/,…,y(n))=0 n-го порядка наз такое его решение у=φ(х,с1,…,сп), кот явл ф-ией переменной х и произвольных независимых постоянных С1,С2,…,Сп. (независимость постоянных означает отсутствие каких-либо соотношений м/д ними). Частным решением дифференциального ур-ния наз решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных С1,С2,…,Сп.
