29. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Структура общего решения

Линейное неоднородное уравнение данного типа имеет вид:

где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

Теорема: Общее решение неоднородного уравнения является суммой общего решения y₀(x) соответствуюшего однородного уравнения и частного решения y₁(x) неоднородного уравнения:

Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.

Метод вариации постоянных

Если общее решение y₀ ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.  Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:

Вместо постоянных C₁ и C₂ будем рассматривать вспомогательные функции C₁(x) и C₂(x). Будем искать эти функции такими, чтобы решение

удовлетворяло неоднородному уравнению с правой частью f(x).  Неизвестные функции C₁(x) и C₂(x) определяются из системы двух уравнений:

Метод неопределенных коэффициентов

Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов.  Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как

1.

2.

где P_n(x) и Q_m(x) − многочлены степени n и m, соответственно.

В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения.  В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель x^s, где s − кратность корня α в характеристическом уравнении.  В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x.  Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.

Принцип суперпозиции

Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида

то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части. 

30.Понятие числового ряда и суммы ряда. Геометрическая прогрессия.

Пусть дана бесконеч.послед-ть чисел a,a..a(1)

Опр-е 1. Выражение (1) назыв. числовым рядом или просто рядом. Числа a,a..aназыв. членами ряда.

Введём понятия суммы ряда, для этого рассмотрим след.суммы:

S= a

S= a+a

S= a+a.. a, S-n-ая частичная сумма ряда.

Т.к. ряд содержит бесконечное число членов, то можно составить последовательность частичных сумм

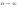Если сущ. Конечный предел послед-ти(S) частичных сумм S=lim S, то этот предел назыв. суммой ряда, а ряд 1 назыв. сходящимся, если сущ. Предел S= a,a..a=

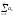
Если предел послед-ти частичных сумм(S) не сущ. или равен бесконечности, то говорят, что ряд суммы не имеет или явл.расходящимся.

30. Понятие числового ряда…:пусть задана посл-ть чисел a₁,a₂,a₃,..,a_n,... .Выражение a₁+a₂+a₃+...+a_n+…+=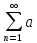_n (1) наз-ся числовым рядом. Числа a₁,a₂,a₃,.. наз членами ряда. 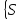a₁-1-й член ряда,a₂-2-й и т.д.Член a_n ряда,стоящий на n-м месте,наз n-м членом ряда или общим.Если задан ряд,то можно сост посл-ть сумм: S₁=a₁,S₂=a₁+a₂,S₃=a₁+a₂+a₃,….,S_n=a₁+a₂+a₃+a_n, кот наз частичными или частными суммами.Сумма 1-х n членов ряда S_n=a₁+a₂+...+a_n наз n-й частичной суммой.Если посл-ть частичных су-м n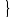 им конеч предел S,т.е. 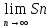=S,то ряд наз сход-ся,а число S сумм-й ряда и пишут _n=S, в против случ ряд наз расх-ся.Числовой ряд a_n+1+a_n+2+....+a_n+k+...=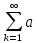_n+k,полу-й из ряда (1) отбрасыванием 1-х n членов,наз оста-м ряда (1) после n-го члена или n-м чл ряда.Для того,чтоб посл-ть b_n б геоме-й прогресс-й,надо и ДОС-но,чтоб для люб n>1 выпо-сь рав-во b²_n=b_n-1b_n+1.Сумма n 1-х чл прогр-и S_n=b₁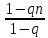,если q≠1; S_n=nb₁, если q=1;S=,если |q|<1.

31.Простей-е св-ва сходящ рядов:1.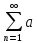_n (1) если этот ряд сход и им S,то ряд 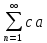_n (2) тоже сход и им сумму (cS) 2.если ряды 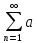_n, 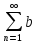_n сход и им соот-о S и S^*,то ряд 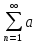_n±b_n тоже сход и им сумму S±S^* 3.схо-ть(рас-ть) ряда не измен,если прибав или отброс люб конеч число членов от его начала : (3) a₁+a₂+a₃+...+a_n+a_n+1+… (4)a_n+1+a_n+2+….Эти ряды сход или расход однов-о для люб фикси-го n. Опр: сумма ряда (4)-ост-к ряда (3) и обоз-ся R_n=a_n+1+a_n+2+… 4.сумму схо-ся ряда м пред-ть в виде суммы:частичн суммы ряда и его ост-ка. 5.если ряд (3) сход,то его ост-к после n-го члена стремит-ся к 0 (R_n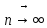0). Нео-й приз сх-ти рядов.Т-ма:если ряд a₁+a₂+...+a_n +(1) сход-ся, то его n-й член стрем к 0 при n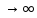,т.е. 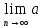_n=0.Сле-е из т-мы:если n-й член ряда не стре-ся к 0 при n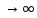,,т.е. 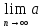_n≠0,то ряд (1) расход. Заме-е:условие 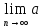_n=0 явл необ-м,но недоста-м,т.е. из выпол-я дан усл невсегда сле-т схо-ть ряда.

32.Интегр-й пр сх-ти:Т-ма:пусть дан полн ряд (1),выполн-ся усл a₁a_2….a_n….Дана непрерыв невозра-я неположит ф-я f(x),заданная для x1,и такая,что f(n)=a_n. Тогда:1.если несобств интеграл 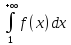схо-ся,то сход и ряд (1) 2.если этот несобств интег-л рас-ся,то расход и ряд (1). Док-во:1. Построим на графике f(x) ступенчатые фигуры как показано на рисунке 2. Площадь большей фигуры равнаS_b=f(1)+f(2)+....+f(n-1) 3. Площадь меньшей фигуры равна S_s=f(2)+f(3)+...+f(n) 4. Площадь криволинейной трапеции под графиком функции равна S_tr=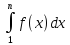5.получаемS_s S_trS_bS_n-a₁S_n-1 6. Далее доказывается с помощью критерия сходимости знакоположительных рядов.