
- •2.Необход и дост условие..:
- •25.Дифференциальные уравнения первого порядка с разделяющимися переменными.
- •26.Линейные дифференциальные уравнения первого порядка.
- •27. Дифференциальные уравнения второго порядка.
- •28.Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •1.Структура общего рещения ур-ия(1)
- •29. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •30.Понятие числового ряда и суммы ряда. Геометрическая прогрессия.
- •33. Признак сравнения для положительных рядов. Признак Даламбера и Коши.
- •38.Ряды Тейлора и Маклорена.
33. Признак сравнения для положительных рядов. Признак Даламбера и Коши.
Признак сравнения:
Пусть даны 2 положительных ряда
 (1) и
(1) и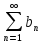 (2)
(2)
Если для всех
номеров n
выполняется неравенство
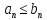 ,
то:
,
то:
1) Из сходимости ряда 2 следует сходимость ряда 1, т.е. из сходимости ряда с большими членами следует сходимость ряда с меньшими членами.
2) Из расходимости ряда 1 следует расходимость ряда 2, т.е. из расходимости ряда с меньшими членами следует расходимость с большими членами.
Признак Даламбера:
Пусть дан положительный ряд
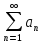 .
Если существует
.
Если существует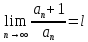 ,
то:
,
то:
1)при
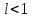 ряд сходится
ряд сходится
2)при
 расходится
расходится
3)
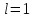 требуются дополнительные исследования
требуются дополнительные исследования
Признак Коши:
Пусть дан положительный ряд
 .
Если существует
.
Если существует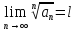 ,
то:
,
то:
1)при
 ряд сходится
ряд сходится
2)при
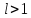 расходится
расходится
3)
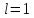 требуются дополнительные исследования
требуются дополнительные исследования
34. Знакопеременные ряды. Абсолютная и условная сходимость.
![]()
![]()
![]()
35. Знакочередующиеся ряды. Признак Лейбница
Знакочередующийся
ряд – это частный случай знакопеременного
ряда (если его члены попеременно
принимают значения противоположных
знаков). Его можно записать в виде:

Признак Лейбница: Если для знакочередующегося ряда выполняются условия:
1)
2)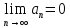
то ряд сходится,
его сумма не превосходит первого члена,
а остаток R
удовлетворяет неравенству
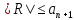
36. Понятие степенного ряда. Область сходимости степенного ряда
Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом:
![]()
Множество значений x, при которых степенной ряд сходится, называется областью сходимости степенного ряда.
Множество значений x, при которых степенной ряд расходится называется областью расходимости степенного ряда.
37.Пусть дан степенной ряд (1) (теорема Абеля):
![]()
1)если степен. ряд сходится при х=х0 ≠0, то он сходится абсолютно при всех х, принадлежащих |x| <| х0|.
2) если при х= х1 степен. ряд расходится, то он расходится при всех х, принадлежащихx|> | х1|.
Замечание1: для каждого степенного ряда (1) сущ-т такое R≥0, что в интервале (-R; R) ряд (1) сходится абсолютно, а в не [-R;R] ряд расходится. В точках ± R ряд может оказаться как сходящимся, так и расходящимся. R – радиус сходимости степенного ряда. (-R; R) – интервал сходимости степенного ряда.
Замечание2: центр интервала сходимости степенного ряда (1):
a0 + a1 (х-х0) + а2(х-х0)2+…+аn(х-х0)n+… находится в точке х0.
Ряд (1) сходится при всех х, удовлетворяющих нерав.|х-х0|<R.
Радиус сходимости м.б. определён по следующей формулам:
![]() (признак
Даламбера).
(признак
Даламбера).
Или
![]() (признак
Коши).
(признак
Коши).
Таким образом, всякий степенной ряд имеет свой радиус сходимости R и интервал расходимости (-R; R) .
При х =± R ряд может либо сходиться, либо расходиться. Этот вопрос реш-ся для каждого ряда индивид-о.
Следствие: согласно сходимости степенного ряда (1), интервалом сходимости является промежуток (-R; R) с возможн. присоед. К нему 1-ой или 2 точками в зависимости от того, как ведёт себя ряд на концах интервала, т.е.при x=R и при x=-R.
