38.Получение мат.Моделей проц-в о эксперимент. Данным

Исходные данные: заранее известные (экспериментальные, наблюденные) значения фактора х_i – экзогенная переменная и соответствующие им значения отклика y_i, (i = 1,…,n) - эндогенная переменная;

Активный и пассивный эксперимент.

Выборочные характеристики – позволяют кратко охарактеризовать выборку, т. е., получить ее модель, хотя и очень грубую:

а) среднее арифметическое:

Среднее арифметическое – это «центр», вокруг которого колеблются значения случайной величины.

процесс эконометрического моделирования можно разбить на шесть основных этапов.

1-й этап (постановочный) - определение конечных целей моделирова­ния, набора участвующих в модели факторов и показателей, их роли;

2-й этап (априорный) - предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда ги­потез;

3-й этап (параметризация) - собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными;

4-й этап (информационный) - сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показате­лей;

5-й этап (идентификация модели) - статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели Непосредственно связан с проблемой идентифицируемости модели, то есть ответа на вопрос «Возможно ли в принципе однозначно восстановить значения неизвестных параметров модели по имеющимся исходным данным в соответст-вии с решением, принятым на этапе параметризации?». После положительного ответа на этот вопрос необходимо решить проблему идентификации модели то есть предложить и реализовать математически корректную процедуру оценива­ния неизвестных параметров модели по имеющимся исходным данным;

6-й этап (верификация модели) — сопоставление реальных и модельных данных, проверка адекватности модели, оценка точности модельных данных.

39. ОЦЕНКИ ПАР-В МОДЕЛИ ПО МНК Модель парной линейной регрессии представляет собой уравнение связи двух переменных x и y вида:

, (1.1)

где x – независимая переменная, y – зависимая переменная (результативный фактор), a, b – параметры регрессии.

Построение уравнения регрессии сводится к оценке его параметров. Для оценки параметров уравнений регрессии используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от его расчетных значений минимальна .

Параметры уравнения (1.1) можно найти по формулам (1.2).

(1.2)

Оценить тесноту линейной связи между факторами x и y можно при помощи коэффициента линейной корреляции, который рассчитывается по формуле (1.3). Коэффициент парной линейной корреляции изменяется в пределах от -1 до 1.

(1.3)

Отрицательное значение коэффициента корреляции говорит об обратной зависимости, а положительное – о прямой. Если абсолютное значение больше 0,7, то говорят о наличии тесной линейной зависимости между факторами x и y.

Качество уравнения определяют нахождением коэффициента детерминации . Его значение показывает, на сколько процентов разброс значений y от средней объясняется зависимостью от фактора x.

Статистическую значимость коэффициентов регрессии можно проверить нахождением t-статистик Стьюдента по формулам (1.4).

(1.4)

S_a и S_b – стандартные ошибки параметров a и b, которые рассчитываются на основе стандартной ошибки уравнения регрессии S.

, , (1.5)

Коэффициент b считается статистически значимым, если . Критическое значение находят по таблицам Стьюдента при уровне значимости (по умолчанию ) и числе степеней свободы n – 2.

Для коэффициента корреляции также можно найти стандартную ошибку и t-статистику (1.6).

. (1.6)

Статистическую значимость уравнения в целом можно оценить при помощи критерия Фишера. Если расчетное значение F > F_кр, то говорят что уравнение регрессии статистически значимо, в противном случае незначимо или неадекватно. F можно рассчитать по формуле (1.7), а F_кр находят по трем параметрам: уровню значимости , числу степеней свободы и количеству независимых переменных 1.

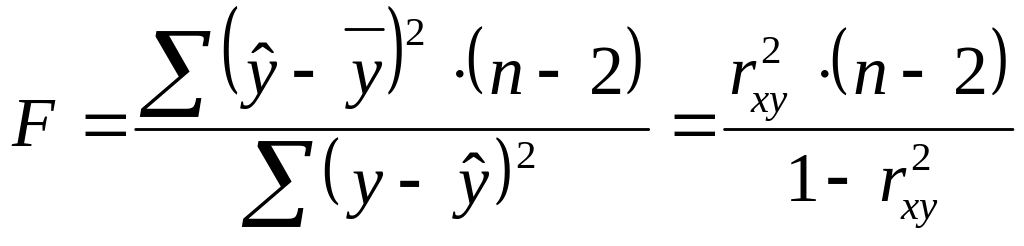(1.7)

Легко доказать, что для парной линейной регрессии , а . Поэтому для парной линейной регрессии оценка адекватности модели равносильна оценке статистической значимости коэффициентов регрессии и корреляции.

Средняя ошибка аппроксимации рассчитывается по формуле (1.8) и характеризует качество уравнения регрессии. Ошибка аппроксимации в пределах 5 – 7% свидетельствует о хорошем подборе модели к исходным данным.

(1.8)

Важной характеристикой является коэффициент эластичности (см. 1.9). Он показывает, на сколько процентов в среднем изменится результат y от своей средней величины при увеличении фактора x на 1% от его среднего значения.

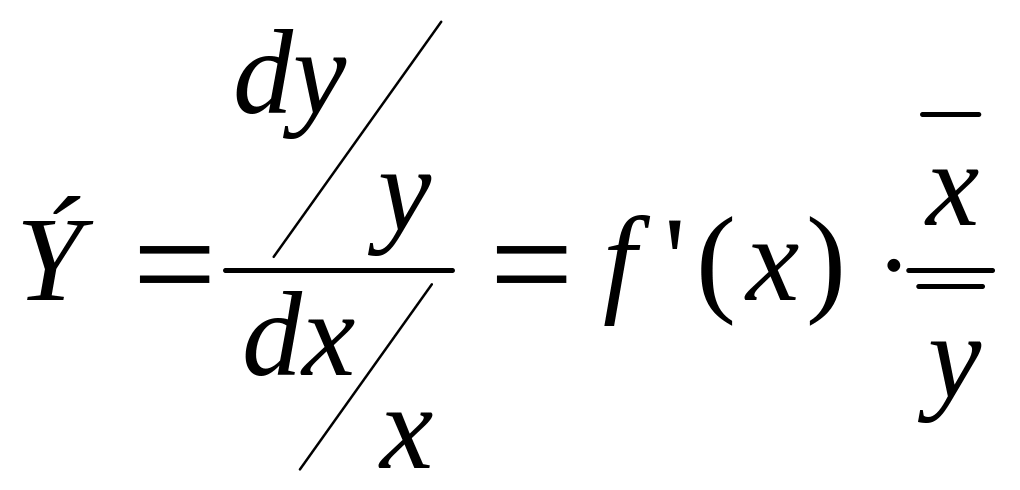. (1.9)

40. МНОЖ.ЛИН.РЕГРЕСС.МОДЕЛЬ Уравнением множественной линейной регрессии называется уравнение вида

, (3.1)

где b₀, b₁, b₂, …, b_m – оценки параметров уравнения регрессии.

Параметры уравнения (3.1) оценивают при помощи МНК. Для линейного уравнения множественной регрессии их можно найти, построив систему нормальных уравнений (3.2).

(3.2)

Решив систему (3.2), получим значения коэффициентов уравнения (3.1). Для n наблюдений уравнение (3.1) можно записать также в матричной форме

, (3.3)

где , , , .

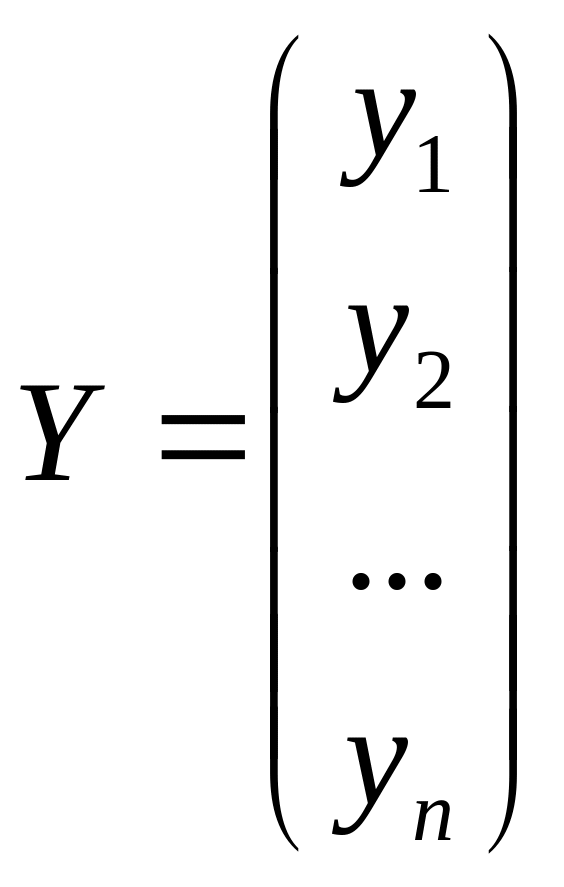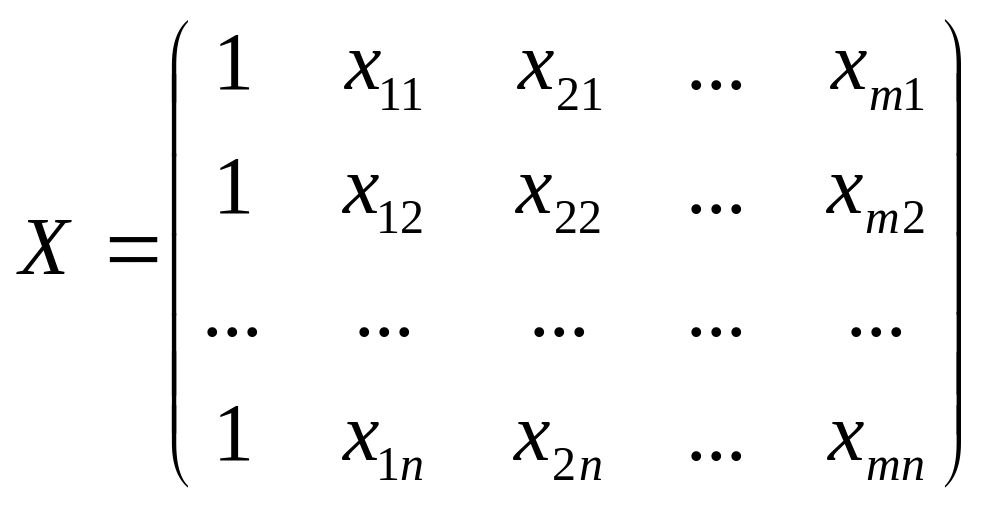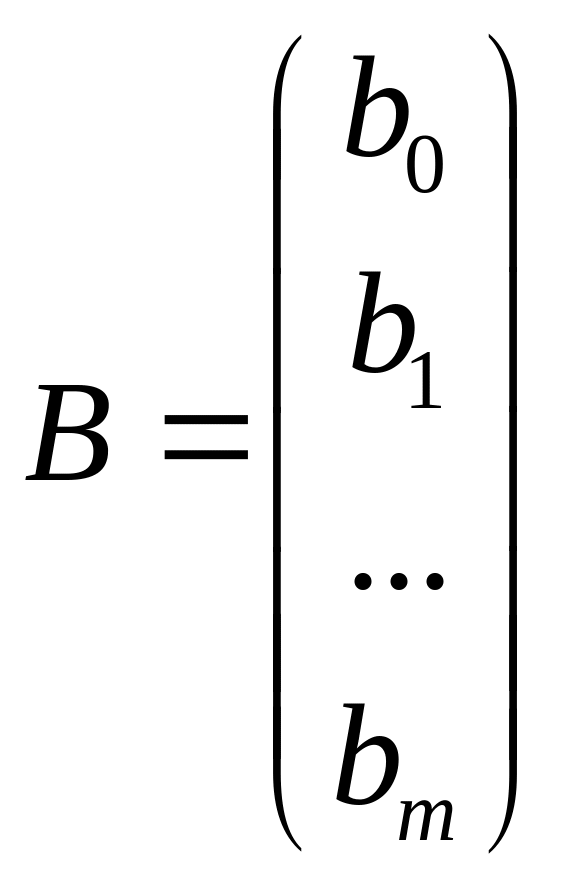Тогда матрицу коэффициентов В можно рассчитать по формуле

, (3.4)

где – матрица, транспонированная к X.

Статистическую значимость коэффициентов уравнения регрессии оценивают на основе расчета t-статистик:

, , , (3.5)

где 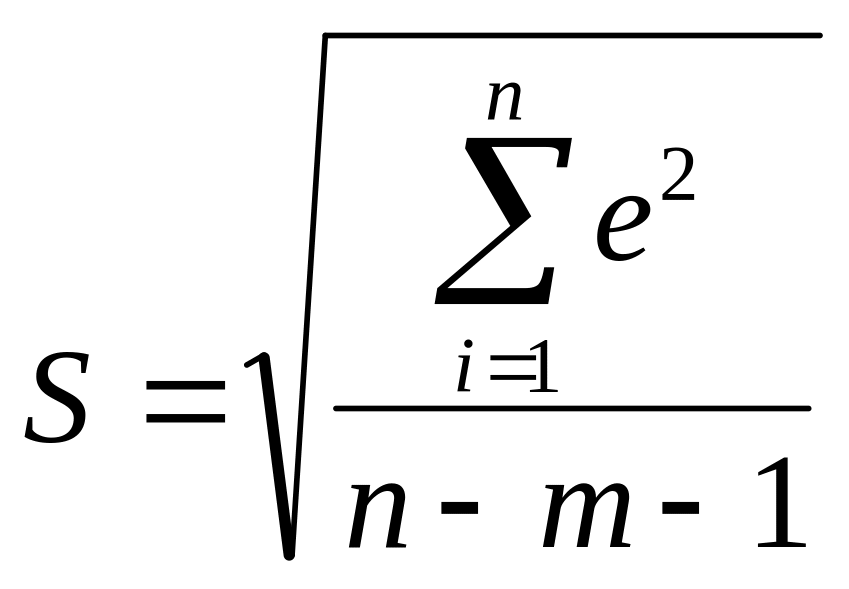– стандартная ошибка уравнения регрессии, – j-й диагональный элемент матрицы , – стандартная ошибка коэффициента .

Качество уравнения регрессии проверяют на основе расчета коэффициента множественной детерминации:

. (3.6)

Коэффициент детерминации показывает, на сколько процентов факторы, включенные в модель регрессии, объясняют вариацию результативного фактора y.

Значимость (адекватность) уравнения регрессии в целом проверяется с помощью F-статистики Фишера:

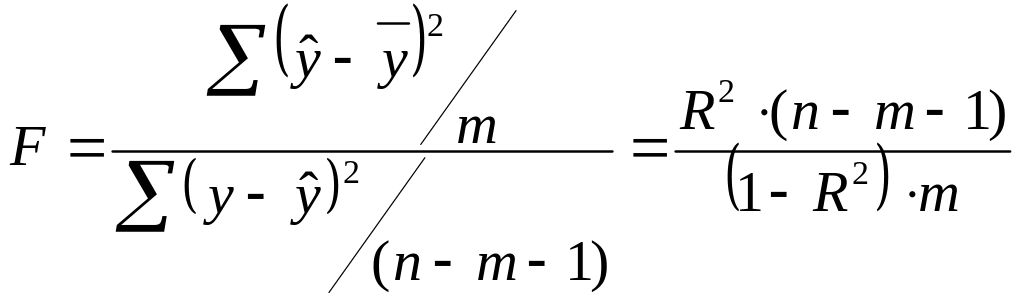. (3.7)

Построенная модель считается адекватной, если расчетное значение . Значение – критическая точка распределения Фишера для уровня значимости  и числа степеней свободы df₁ = m, df₂ = n – m – 1, где m – число независимых переменных, n – число наблюдений.

При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности, т.е. тесной линейной зависимости, независимых факторов. Считается, что переменные x_i и x_j явно коллинеарны, если частный коэффициент линейной корреляции . Этот коэффициент легко найти, используя формулу (1.3). Простейшим способом устранения мультиколлинеарности является включение в модель только тех факторов, которые при достаточно тесной связи с результатом имеют наименьшую зависимость между собой.

Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле:

. (3.8)

Для построения уравнения множественной регрессии можно также использовать линеаризуемые функции:

• степенная – ,

• экспоненциальная – ,

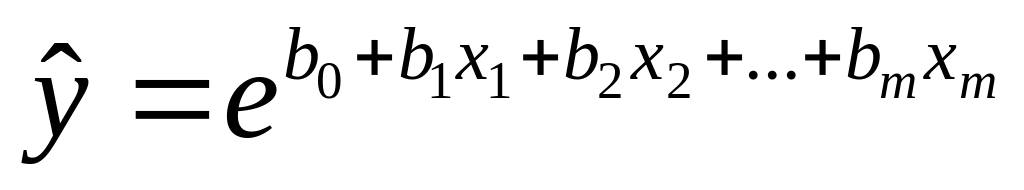• гиперболическая – .
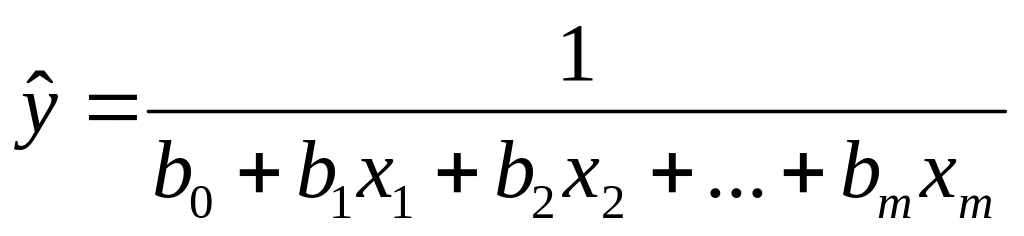