15 В каком случае двумерная задача программирования не имеет решения

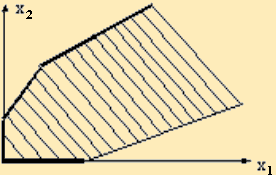
Неосновной случай - получается неограниченный (незамкнутый) выпуклый многоугольник, имеющий вид, подобный изображенному на рис.

Возможен случай, когда неравенства противоречат друг другу, и допустимая область вообще пуста.

если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.

16 Как находится линия уровня

Если область допустимых решений является непустым множеством, построить нормаль линий уровня n = (c1 ,c2 ) и одну из линий уровня, имеющую общие точки с этой областью.

17В чем отличие задач нахождения максимума целевой функции от задач нахождения минимума целевой функции

Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум- в противоположном направлении.

Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения в виду неограниченности целевой функции.

Если задача линейного программирования имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки c соответствующей опорной прямой.

Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычислить значение целевой функции на этих решениях.

20Почему симплекс-метод считается основным в задачах линейного программирования

Известно, что оптимальное решение задачи лин.программирования связано с угловыми точками многогранника решений. Угловых точек может быть много, если много ограничений, количество угловых точек соответствуют количеству базисных решений. Для каждого базисного решения однозначно определяется значение целевой функции. В связи с этим необходим такой переход от одного базисного решения к другому, в результате которого новое решение приносило бы невырожденной задаче на максимум больше значение целевой функции, а в невырожденной задаче на минимум меньше. Данный процесс решения задачи реализует симплекс-метод, который называется методом последовательного улучшения плана. Процесс решения задачи продолжается до получения оптимального плана, либо до установления факта отсутствия решения задачи.

Если задача лин программирования вырожденная, то при переходе от одного базисного решения к другому, значение целевой функции может не измениться.

Переход от одного базисного решения к другому называется итерацией симплекс-метода(шагами).

Симплекс-метод – основной в линейном программировании. Решение задачи начинается с рассмотрения одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней вершине, увеличивая значение функции цели при решении задачи на максимум и уменьшая на при решении на минимум. Т.о. переход от одной вершине к другой улучшает значение функции цели. Т.к число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима. Для использования симплекс-метода необходимо привести задачу к каноническому виду. Система ограничений здесь - система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные.

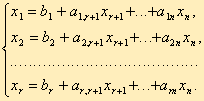
К такому виду можно привести любую совместную систему, например, методом Гаусса.

Фундаментальная теорема симплекс-метода: среди оптимальных планов задачи лин программирования в канонической форме обязательно есть опорное решение её системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение Z самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.