32) Формулы Крамера.

Метод Крамера — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А

D = det (ai j)

и n вспомогательных определителей D i (i= ), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.

Формулы Крамера имеют вид:

D × x i = D i ( i  = ).                                                (5.4)

Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:

x i = D i / D.

Если главный определитель системы D и все вспомогательные определители D i = 0 (i= ), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

33) Теорема Кронекера-Капелли.

Для того чтобы система линейных уравнений AX = B была совместной, необходимо и достаточно, чтобы ранг её матрицы был равен рангу расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Система совместна, если rangA = rangD. Очевидно, что система (1) может быть записана в виде:

x₁ + x₂ + … + x_n

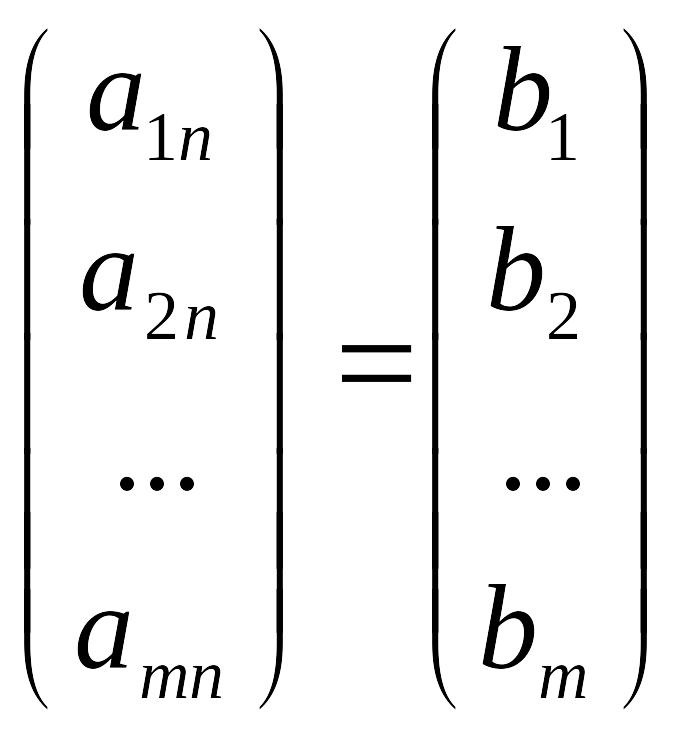
Доказательство.1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А^* не изменяют ранга.2) Если RgA = RgA^*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

34) Условия определенности и неопределенности систем линейных уравнений.

Совместная система линейных уравнений называется определенной, если имеет только одно решение. В противном случае система линейных уравнений называется неопределенной.

35) Метод Гаусса.

Метод Гаусса – метод последовательного исключения искомых неизвестных величин. С помощью элементарных преобразовании строк расширенной матрицы D системы, матрицу А приводят к ступенчатому виду.

Гаусс.

Любую систему такого вида можно привести к равносильной ей разрешенной системе.2 системы равносильны, если имеют одно и то же множество решений. Преобразование переводящее систему 1 в разрешенную называется джордановыми. В результате работы алгоритма Гаусса слева будут стоять неизвестные, а справа числа и свободные переменные. Это решение общее. Придавая свободным разные числовые решения, получаем частные решения.

36) Теорема о совместности однородной системы линейных уравнений.

Вместе с 37

3 7) Теорема о существовании ненулевых решений однородных систем линейных уравнений.

38)Линейное векторное пространство.

Множество L  называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:

1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y, причём:

x + y = y + x − сложение коммутативно;

x + (y + z) = (x + y) + z − сложение ассоциативно;

x + 0 = x − существует единственный нулевой элемент 0 ( x + 0 = x для любого x из L);

x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x ( x + (−x) = 0 для любого x из L).

2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x, причём:

α·(β·x) = (α·β)·x − умножнение на число ассоциативно: ;

1·x = x − для любого элемента x из L.

3. Операции сложения и умножения на число связаны соотношениями:

α·(x + y) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;

(α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.