28)Понятие дифференцируемости функции
Определение. Функция y=f(x) называется дифференцируемой в точке х, если ее приращение Δу в этой точке можно представить в виде
,
где А –
некоторое число, не зависящее от 
,
а α(
)
– функция аргумента
,
являющаяся бесконечно малой при 
→0,
т.е. 
Выясним теперь связь между дифференцируемостью в точке и существованием производной в той же точке.
Теорема. Для того чтобы функция f(x) была дифференцируемой в данной точке х , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Связь между дифференцируемостью функции и ее непрерывностью
Пример. Доказать, что функция y=│х│ недифференцируема в точке х=0 .
Решение. Производная функции (если она существует) равна
Очевидно,
что при х=0
производная не существует, так как
отношение 
,
т.е. не имеет предела при Δх→0
(ни конечного,
ни бесконечного). Геометрически это
означает отсутствие касательной к
кривой в точке х=0.
Теорема. Если функция y=f(x) дифференцируема в точке х0,, то она в этой точке непрерывна.
□Доказательство. По условия функция y=f(x) дифференцируема в точке х0, т.е. существует конечный предел
где f′(x0)
– постоянная величина, не зависящая
от 
.
Тогда на основании теоремы о связи бесконечно малых величин с пределами функций можно записать
где α(∆х) является
бесконечно малой величиной при 
→0,
или
.
При Δх→0 на основании свойств бесконечно малых величин устанавливаем, что Δу→0 и, следовательно, по определению непрерывности функции в точке, делаем вывод, что функция непрерывна в токе х0. ■
Обратная
теорема, вообще говоря, неверна, если
функция непрерывна в данной точке, то
она не обязательно дифференцируема
в этой точке. Так, функция y=│х│
непрерывна в точке х0=0,
ибо 
но,
как было доказано ранее недифференцируема
в этой точке.
Таким образом, непрерывность функции – необходимое, но не достаточное условие ее дифференцируемости.
Замечание: Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором промежутке Х, то функция называется гладкой на этом промежутке. Если же производная функция допускает конечное число точек разрыва, то такая функция на данном промежутке называется кусочно гладкой.
29)
30) 1. Производная от числа
С'=0
2. Производная от корня
3. Производная от функции в степени
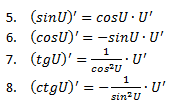
5. Производная от степенной функции, показательной функции, от логарифма, от натурального логарифма
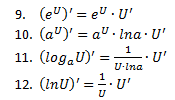
6. Производная от арксинуса, арккосинуса, арктангенса, арккотангенса (производная от arcsinx, arccosx, arctgx, arcctgx)
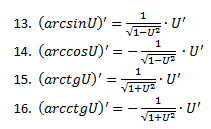
7. Производная сложной функции (производная от х в степени х)
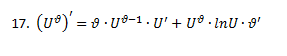
8. Производная от функции, заданной параметрически
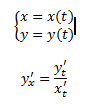
9.Производная от частного, суммы, произведения
Таблица производных
Элементарные функции |
Сложные функции |
С’=0 |
|
(xn)’=nxn-1 |
(Un)’=n*un-1*u’ |
(ax)’=ax*lna |
(au)’=au ln a *u’ |
(ex)’=ex |
(eu)’=eu*u’ |
Logax=1/(x ln a) |
Logau=1/(u ln a) * u’ |
(ln x)’=1/x |
(ln u)’=1/u*u’ |
(sin(x))’=cos(x) |
(sin(u))’=cos(u)*u’ |
(cos(x))’=-sinx |
(cos(u))’=-sinu*u’ |
(tg(x))’=1/cos2x |
(tg(u))’=1/(cos2u)*u’ |
(ctg(x))’=-1/(sin2x) |
(ctg u)’=-(1/sin2u)*u’ |
(arctg(x))’=1/(1+x2) |
|
(arctg(x))’=-1/(1+x2) |
|
(arcsin(x))’=1/sqrt(1-x2) |
|
(arcos(x))’=-1/sqrt(1-x2) |
|
31) Теорема о производной сложной функции:
Если
функция 
имеет
производную 
в
точке 
,
а функция 
имеет
производную 
в
соответствующей точке
,
то сложная функция 
имеет
производную 
в
точке
,
которая находится по формуле 
.
Доказательство:
По
условию 
. Отсюда,
по теореме о связи функции, её предела
и бесконечно малой функции, имеем 
или 
,
где 
при 
.
Функция
имеет
производную в точке
: 
,
поэтому:
,
где 
при 
.
Подставив
значение 
в
равенство
,
получим: 
; 
.
Разделим полученное равенство на 
и
перейдя к пределу при
,
получим
.
Пример:
Найти
производную 
.
Решение: 
.
32) Теорема о производной обратной функции:
Если
функция 
строго
монотонна на интервале 
и
имеет неравную нулю производную 
в
произвольной точке этого интервала, то
обратная ей функция
также
имеет производную 
в
соответствующей точке, определяемую
равенством 
или 
.
Доказательство:
Рассмотрим
обратную функцию
.
Дадим аргументу приращение 
.
Ему соответствует приращение 
обратной
функции, причем 
в
силу строгой монотонности функции.
Поэтому можно записать: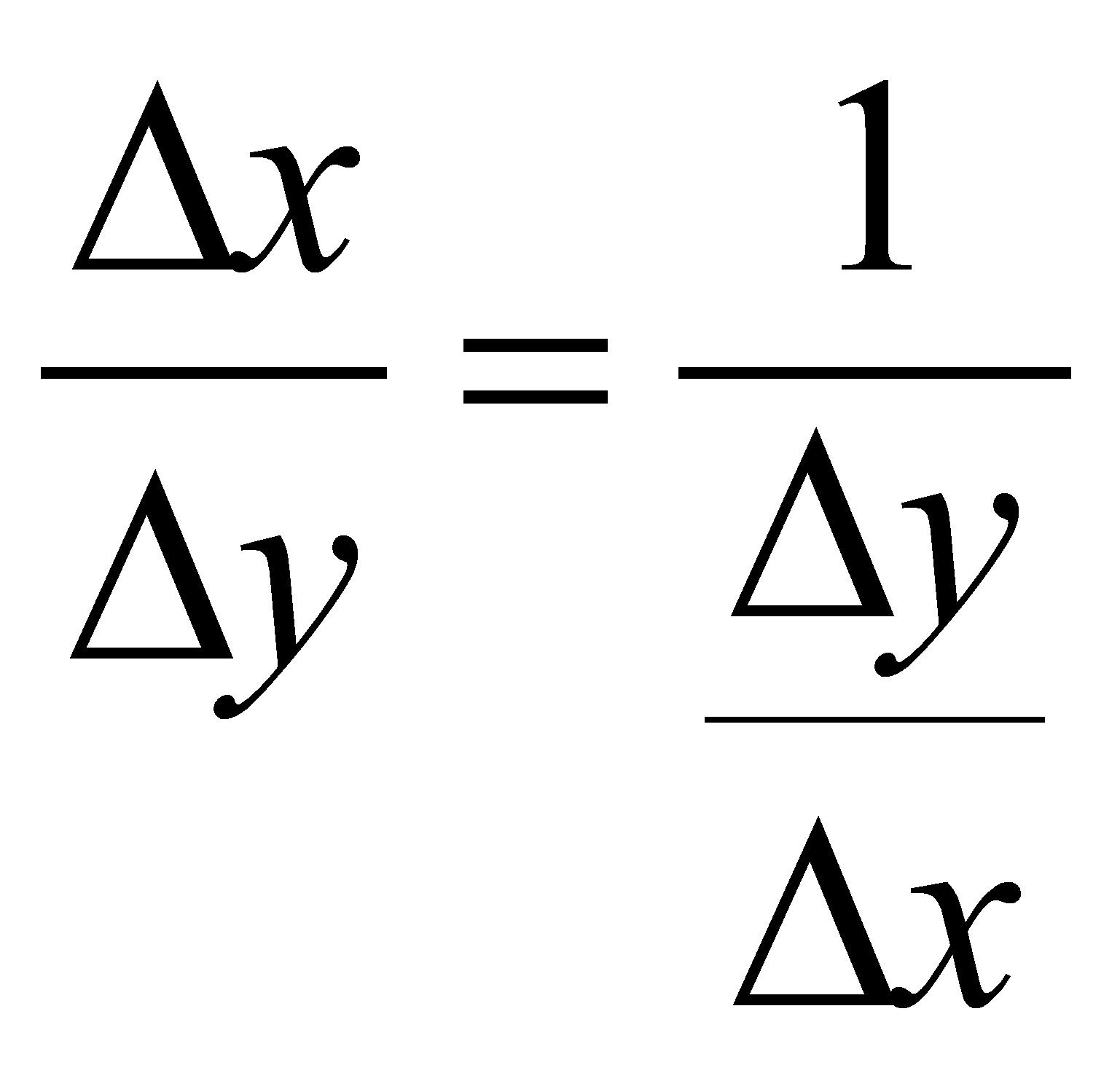 
.
Если 
,
то, в силу непрерывности обратной
функции, 
.
И т.к. 
,
то из
следует
равенство: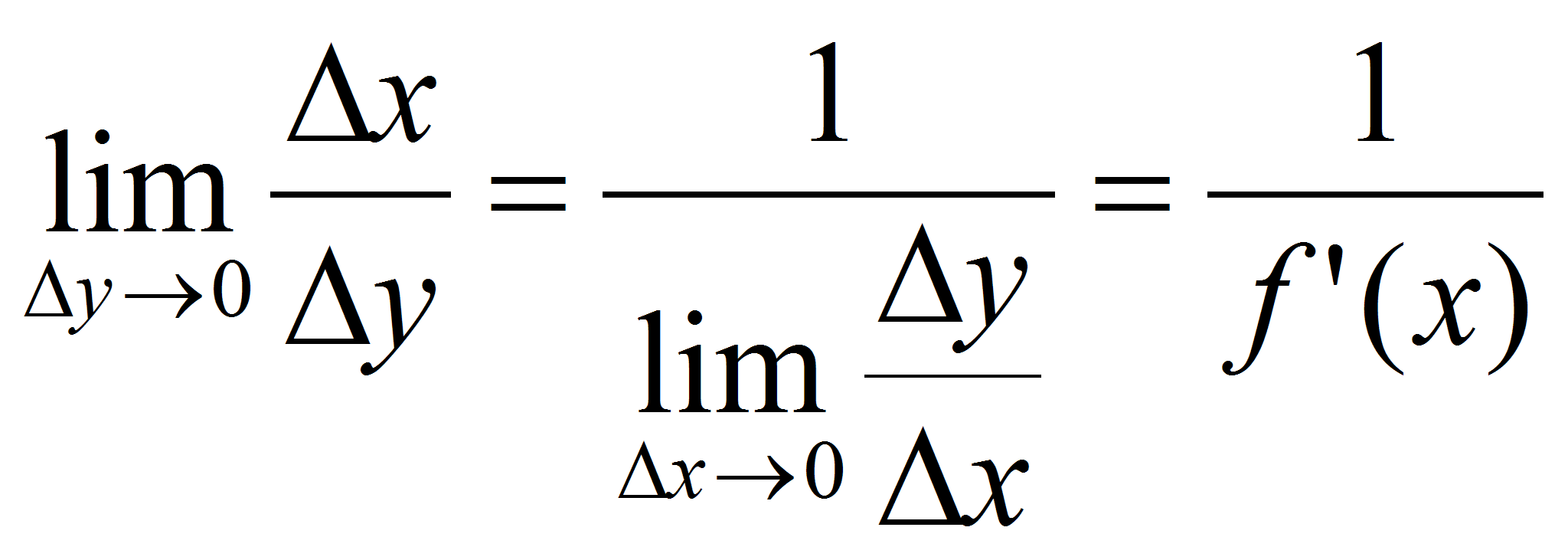 
,
т.е. 
.
33) 1) Функция называется дифференцируемой в данной точке, если в этой точке существует ее производная.
2)Определение 4 (дифференцируемость в точке). Функция f(x) называется дифференцируемой в точке x, если приращение y этой функции в точке x представимо в виде
y =A x + ( x) x, |
(1) |
где A - некоторое число, не зависящее от x, а lim x 0 ( x ) = 0.
В дальнейшем будем считать, что (0) = 0. В этом случае функция (x) будет непрерывной в точке x = 0. Равенство 1 можно переписать иначе, так как функции ( x), x - бесконечно малые в точке x = 0 и их произведение тоже бесконечно малая функция, поэтому
y =A x +o( x). |
(2) |
Справедлива теорема
Теорема 1. Для того чтобы функция была дифференцируема в точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство. Необходимость. Пусть функция дифференцируема, тогда ее приращение представимо в виде (1). Поделив (1) на x 0 получим
y/ x = A+( x).
Переходя к пределу в последнем выражении при x 0, получим, что A=f'(x).
Достаточность. Пусть существует конечная производная f'(x), то есть существует конечный предел
lim x 0 y/ x = f'(x).
Обозначим ( x) = y/ x-f'(x). Отсюда вытекает представление (1).
Пример 4. Доказать, что функция |x| не дифференцируема в точке x = 0.
Решение. Найдем приращение функции в точке x = 0 :
y = | x|
Поэтому
lim x -0 y/ x = -1, lim x +0 y/ x = 1,
следовательно, функция |x| в точке x = 0 не дифференцируема.
Следующая теорема выражает связь между непрерывностью и дифференцируемостью.
4)Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке.
При этом
|
Δy = f(x0+Δx)-f(x0) = f '(x0)Δx+α(Δx)Δx, |
|
где α(Δx) - бесконечно малая функция, при Δx→0.
5) ТЕОРЕМА (о необходимом и достаточном условии дифференцируемости функции в точке)
;
(
–
дифференцируемая в точке 
) 
.
Доказательство.
(
)
По определению дифференцируемости
функции в точке имеем 
;
отсюда
при 
получаем 
.
Поскольку 
,
то, применив теорему о пределе суммы,
устанавливаем существование 
.
Итак, для дифференцируемой в точке функции ее приращение представимо в виде
.
(
)
Если существует 
,
то существует 
,
т.е. 
–
бесконечно малая функция при 
.
Отсюда 
и
здесь 
, 
при
,
т.е. 
.
Полученное
представление для 
доказывает
дифференцируемость функции по определению.
34) Дифференциалом функции y=f(x) в точке x называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dy или (df(x)):
dy=f ‘ (x) * dx
(Дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной).
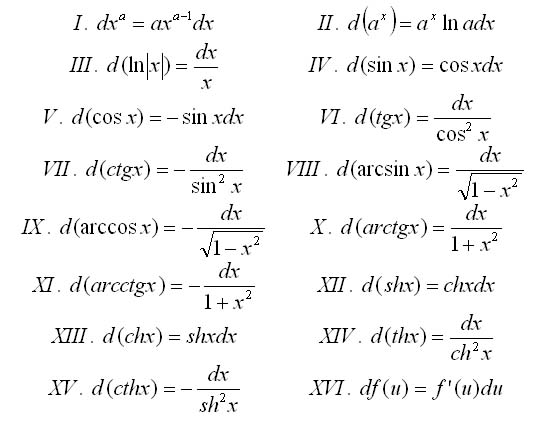
Дифференциал функции обладает свойствами, аналогичными свойствам производной.
Дифференциал постоянной равен нулю: dc = 0, с = const.
Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:
d(u+v)=du + dv
Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
d(u+c) = du (c= const).
Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
d(uv) = udv + vdu.
Следствие. Постоянный множитель можно выносить за знак дифференциала
d(cu) = cdu (с = const).
Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой
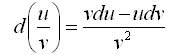
Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.
2)
(С
– постоянная величина)
Геометрический смысл дифференциала:
Дифференциал функции y=f(x) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение Δx.
35) Установленное в первом параграфе приближенное равенство
(тут у меня картинка, но она не отобразилась на сайте))
или
(14)
позволяет использовать дифференциал для приближенных вычислений значений функции.
Запишем приближенное равенство более подробно. Так как
а
то
или
(15)
Пример 3. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.
Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (15) в данном случае примет вид
Положим
тогда
Следовательно,
что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.
Пример 4. Пользуясь понятием дифференциала, вычислить приближенно
Решение.
Число
является
одним из значений функции
Так как производная этой функции
то формула (15) примет вид
Полагая
и
получаем
(табличное значение
).
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная
погрешность 
приближенного
числа 
равна
абсолютной величине разности между
точным числом 
и
его приближенным значением:
(16)
Относительной
погрешностью 
приближенного
числа
называется
отношение абсолютной погрешности этого
числа к абсолютной величине соответствующего
точного числа:
(17)
Если точное число неизвестно, то
(18)
Иногда,
прежде чем применить формулу (15), требуется
предварительно преобразовать исходную
величину. Как правило, это делается в
двух целях. Во-первых, надо добиться,
чтобы величина
была
достаточно малой по сравнению с 
,
так как чем меньше 
,
тем, вообще говоря, точнее результат
приближенного вычисления. Во-вторых,
желательно, чтобы величина 
вычислялась
просто.
Пример
5. Пользуясь
понятием дифференциала, вычислить
приближенно 
.
Оценить точность полученного результата.
Решение. Рассмотрим функцию
Её производная равна
а формула (15) примет вид
В данном случае было бы нерационально вычислять приближенно следующим образом:
так как значение
не является малым по сравнению со значением производной в точке
Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда
Теперь, полагая
получим
Умножая на 4/3, находим
Принимая табличное значение корня
за точное число, оценим по формулам (16) и (17) абсолютную и относительную погрешности приближенного значения:
