1.Декартова система координат (квадратная) и полярная система. 3

2. Понятие геометрического вектора. Основные определения. 4

3. Линейные операции над векторами 5

4. Деление отрезка в заданном отношении 6

5. Понятие о радиус-вектора 7

6. Действие с геометрическими векторами в координатной форме. Признак коллениарности. 8

7. Скалярное произведение геометрических векторов. Признаки ортогональности 9

8. Вычисление скалярного произведения векторов через их координаты, длина вектора, расстояние между двумя точками, вычисление косинуса угла между двумя векторами. 10

9. Направляющие косинусы и их свойства. 11

10. Общее уравнение прямой на плоскости 12

11. Уравнение прямой с угловым коэффициентом. Геометрический смысл коэффициентов. Пучок прямых 13

12. Уравнение прямой, Проходящей через две заданные точки на плоскости и в пространстве. 14

13. Угол между прямыми. Условия параллельности и перпендикулярности, прямой на плоскости. 15

14. Общее уравнение плоскости 16

15) Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей 17

16)Уравнение прямой в пространстве, проходящей через две точки 18

17) Условия параллельности и перпендикулярности прямых в пространстве 19

18) Условия параллельности и перпендикулярности прямой и плоскости в пространстве. 20

19) Угол между прямой и плоскостью 21

20) Окружность 22

24. Матрица и основные определения связанные с ней. 23

25. Действия с матрицами 24

26. Определения определителя и его свойства. 25

27. Определения минора и алгебраического дополнения 26

28. Обратная матрица. 27

29. Определения ранга матрицы 28

30. Система линейных уравнений. Определение совместной, не совместной системы 29

31) Матричный способ решения систем линейных уравнений. 31

32) Формулы Крамера. 32

33) Теорема Кронекера-Капелли. 33

34) Условия определенности и неопределенности систем линейных уравнений. 34

35) Метод Гаусса. 35

36) Теорема о совместности однородной системы линейных уравнений. 36

37) Теорема о существовании ненулевых решений однородных систем линейных уравнений. 37

38)Линейное векторное пространство. 38

39.1.Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними 39

40. Линейная зависимость и независимость системы векторов. Пусть имеется n векторов. 40

41. Система векторов линейного пространства L образует базис в L если эта система векторов упорядочена, линейно независима и любой вектор из  L линейно выражается через векторы системы. 41

42. Теорема. (О разложении вектора по базису.) 42

43. Подпространство 43

44. Собственные числа и собственные вектора 44

45. Характеристическим уравнением матрицы 46

1.Декартова система координат (квадратная) и полярная система.

Орты: i_(x) j_(y) k_(z) – Д.

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.

2. Понятие геометрического вектора. Основные определения.

Вектором называется направленный отрезок прямой с началом в точке А, концом в точке В (например), тогда обозначается как .

2 вектора равны, если они коллинеарны, если они лежат на одной прямой или на параллельных прямых.

Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой. Могут быть сонаправлены, а могут быть противоположно направлены.

Нулевой вектор (нуль-вектор) — вектор, начало которого совпадает с его концом. Нулевой вектор имеет норму 0 и обозначается или .

Три вектора (или большее число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.

Единичным вектором (орт-вектором) называется вектор, абсолютная величина (модуль) которого равен единице индекс е. Задан вектор а, вектор ае - единичный. Этот единичный вектор направлен туда же, куда направлен и сам вектор а, и его модуль равен единице, (ае = 1).

Длина (модуль) вектора — скаляр, равный арифметическому квадратному корню из суммы квадратов координат (компонент) вектора.

3. Линейные операции над векторами

4. Деление отрезка в заданном отношении

5. Понятие о радиус-вектора

Радиус-вектором точки называется вектор, начало которого всегда совпадает с началом системы координат, а конец - с данной точкой.

Единичные векторы. направленные по координатным осям O_x O_y O_z называются ортами координатных осей. По теореме о разложении по базису для арифметических векторов справедливо равенство. (a_x;a_y;a_z)= a_x (1;0;0) + a_y (0;1;0) + a_z (0;0;1), которому соответствует равенство для геометрических векторов = а_x + a_y + a_z

6. Действие с геометрическими векторами в координатной форме. Признак коллениарности.

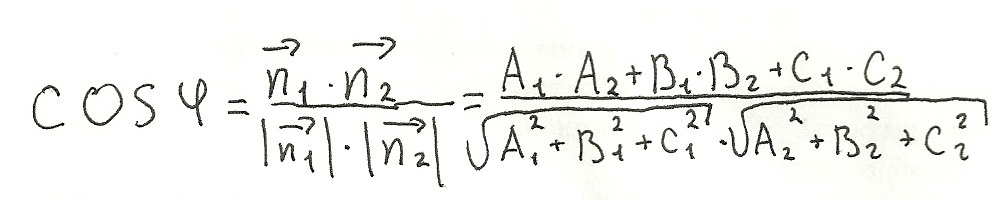
Признак коллинеарности векторов:

n₁||n₂; n₂= λn₁; (A₂,B₂)= λ(A₁,B₁); A₂=λA₁; B₂=λB₁; A₂/A₁=B₂/B₁=λ

7. Скалярное произведение геометрических векторов. Признаки ортогональности

.

Признак ортогональности векторов:

y=k₁x+b₁; k₁=tgφ₁; y=k₂x+b₂ k₂=tgφ₂; n₁=(A1B1); n₂=(A₂B₂); n₁n₂=A₁A₂+B₁B₂ =0

8. Вычисление скалярного произведения векторов через их координаты, длина вектора, расстояние между двумя точками, вычисление косинуса угла между двумя векторами.

Скалярное произведение может быть вычислено по формуле

.

Длина вектора – это скаляр, равный арифметическому квадратному корню из суммы квадратов координат (компонент) вектора.

Расстояние d между двумя точками ( , , ) и ( , , ) в пространстве определяется формулой

.

С калярным произведением двух векторов называется произведение длин двух векторов на косинус угла между ними.

9. Направляющие косинусы и их свойства.

Направляющими косинусами прямой называются направляющие косинусы вектора , которые могут быть вычислены по формулам:

;     .

10. Общее уравнение прямой на плоскости

Общее уравнение прямой на плоскости Ax + By + C

11. Уравнение прямой с угловым коэффициентом. Геометрический смысл коэффициентов. Пучок прямых

- уравнение прямой с угловым коэффициентом

k - угловой коэффициент прямой, равный тангенсу угла, образованного прямой с положительным направлением оси абсцисс (угол измеряется против часовой стрелки)

- уравнение пучка прямых

12. Уравнение прямой, Проходящей через две заданные точки на плоскости и в пространстве.

Пусть в пространстве заданы две точки M₁(x₁, y₁, z₁) и M₂(x_2, y₂, z₂), тогда уравнение прямой, проходящей через эти точки:

                                                

            Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

            На плоскости записанное выше уравнение прямой упрощается:

13. Угол между прямыми. Условия параллельности и перпендикулярности, прямой на плоскости.

Угол между прямой и плоскостью

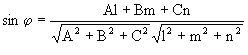
Условие параллельности прямой и плоскости

Аl + Вm + Сn = 0

Условие перпендикулярности прямой и плоскости

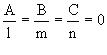
14. Общее уравнение плоскости

Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0, где А, В, С – координаты вектора

15) Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей

Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j1 соотношением: j = j1 или j = 1800 - j1, т.е.

cosj = ±cosj1.

Определим угол j1. Известно, что плоскости могут быть заданы соотношениями:

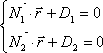
, где (A1, B1, C1), (A2, B2, C2). Угол между векторами нормали найдем из их скалярного произведения:

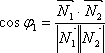
Таким образом, угол между плоскостями находится по формуле:

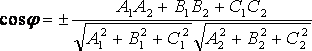
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.

Условия параллельности и перпендикулярности плоскостей

На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.

Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

Плоскости параллельны, векторы нормалей коллинеарны: ïï .Это условие выполняется, если: A₁/A₂=B₁/B₂=C₁/C₂