394026 Воронеж, Московский просп., 14

9. Подобие гидромеханических процессов

Теория подобия получила общее признание, как простейший метод решения некоторых теоретических задач и как основа строгого научного экспериментального исследования гидродинамических процессов на моделях. Результаты эксперимента на моделях могут быть соответствующим образом перенесены на натуру только при условии соблюдения законов подобия.

Аналогично известному представлению о геометрическом подобии, сохранение которого означает, что отношение соответствующих геометрических размеров подобных тел есть величина постоянная, все процессы переноса будут подобными, когда такое отношение будет сохраняться нс только для линейных размеров, но и для всех других величин, определяющих эти явления (время, скорость, сила, давление, плотность, температура и т. д.).

Для установления законов подобия разделим все экспериментально изучаемые явления и процессы на две группы. Первая группа это процессы, которые математически описаны, т. е. дифференциальные уравнения этих процессов существуют. Опыты же проводятся для того, чтобы найти пути решения этих уравнений или сравнить результаты эксперимента с решениями уравнений, если они получены. Другая группа процессов и явлений еще не имеет уравнений, их описывающих. Тогда опыты ставятся для того, чтобы установить законы, управляющие исследуемыми явлениями, записать эти законы в виде некоторых математических соотношений и распространить указанные результаты на случаи, для которых эксперимент не производился.

В зависимости от того, к какой группе относится изучаемое явление, определяется метод нахождения безразмерных параметров, называемых числами подобия. Если уравнение дано (хотя и нет его решений), то числа подобия, как будет показано далее, легко находятся из анализа уравнений. В начальной стадии изучения некоторых сложных явлений, когда еще нет описывающих их уравнений, а иногда нет вообще математической постановки задачи, единственным методом получения чисел подобия, определяющих процесс, является теория размерности.

На примере уравнений гидромеханики рассмотрим метод анализа уравнений и основы теории размерностей.

Для выяснения условий, при соблюдении которых уравнения движения будут одинаковы или движения подобны, напишем уравнения Стокса (X. 7) для плоского случая в безразмерном виде. В качестве масштаба длины выберем какой-либо характерный размер тела l (хорда крыла, диаметр или радиус трубы и др.), а масштабами скоростей, давлений, плотности, температуры и пр. - их характерные значения (на бесконечности, средние по объемным, массовым расходам и пр.).

Обозначая безразмерные величины теми же буквами, что и размерные, но с черточкой, произведем следующую замену:

За масштаб времени взято время, характерное для данного движения, а за масштаб массовых сил, отнесенных к единице массы - ускорение силы тяжести.

После подстановки написанных выражений в (X. 7) получим уравнения плоского движения и уравнение неразрывности

;

;

.

Разделив первые два уравнения на и третье на и опустив для простоты письма черточки над буквами, получим

;

;

.

Из этой системы следует, что если два потока подобны, т. е. они определяются одинаковыми уравнениями и одинаковыми граничными и начальными условиями, представленными в безразмерном виде, то для этих двух потоков должны быть одинаковы следующие безразмерные величины:

.

Обычно в теории подобия пользуются комбинациями указанных величин, каждая из которых имеет свое название и обозначается следующим образом:

- число Струхаля;

- число Фруда;

- число Эйлера;

- число Рейнольдса.

Условие одинаковости чисел, характеризующих подобие, обозначается словом idem, т.е. Sh = idem, Re = idem и т.д.

Число Эйлера для сжимаемой жидкости

,

где - скорость звука;

- показатель адиабаты;

М - отношение скорости потока к скорости звука.

Следовательно, число Eu для сжимаемой жидкости заменяется числами k и М. Используя уравнение энергии в безразмерном виде, можно показать, что каждая из этих величин в отдельности должна быть одинакова для двух подобных потоков, т.е. k = idem и М = idem. Таким образом, в подобных потоках сжимаемой жидкости будет

Sh = idem, Re = idem, Fr = idem, M = idem и = idem.

Если бы не было уравнений движения, то указанные числа подобия так же, как и числа подобия любых физических явлений можно получить из теории размерности.

Размерность данной физической величины определяется соотношением между ней и теми физическими величинами, которые приняты за основные. В каждой системе единиц имеются свои основные единицы. В международной системе единиц основными являются: длина - метр, масса - килограмм, время - секунда, сила электрического тока - ампер, термодинамическая температура - градус Кельвина и сила света - свеча.

Размерность остальных физических величин, так называемых производных единиц, принимается на основании физических законов, устанавливающих связь между ними. Эта связь может быть представлена в виде формулы, называемой формулой размерности.

Теория размерностей основана на двух положениях:

1) отношение двух численных значений какой-нибудь производной величины не зависит от выбора масштабов для основных единиц измерения. Например, отношение двух площадей не зависит от того, в каких единицах будут измеряться площади;

2) всякое физическое соотношение между размерными величинами можно сформулировать как соотношение между безразмерными величинами. Это положение в теории размерности называют П-теоремой.

Не приводя доказательств, укажем, что из первого положения следует, что формулы размерности физических величин должны иметь вид степенных одночленов, т.е.

,

где и - размерность основных единиц.

Математическое выражение П-теоремы можно представить в таком виде: если размерная величина а является функцией независимых между собой размерных величин , т.е.

,

где - число основных размерных величин, то безразмерных комбинаций Пi указанных размерных величин могут быть представлены в виде

;

;

................................

.

Для примера установим зависимость коэффициента сопротивления крыла , рассмотренного в п. 8, гл. VII. Допустим, что зависит от следующих размерных величин: плотности , вязкости , скорости полета V и линейного размера крыла l. Тогда

.

Пользуясь формулой размерности, можно найти безразмерную комбинацию указанных физических величин, представив их размерность степенным одночленом

.

Для нахождения показателей a, d, с и п подставим в эту формулу значения размерностей физических величин в некоторой системе единиц. Выберем международную систему СИ. Тогда будем иметь

.

Подставив эти величины в степенной одночлен, получим

,

откуда относительно основных единиц измерения будем иметь три следующих уравнения

для кг: a + d = 0;

для м: - 3a - d + c + n = 0;

для сек:- в - с = 0.

Решим эту систему, считая один из показателей степени, например п, известным. Получим а = с = п; d = - п. Таким образом, найдем безразмерную величину, от которой зависит

.

Следовательно, зависит от числа Re. Показатель степени числа Re можно найти из эксперимента или каких- либо дополнительных соображений о механизме сопротивления крыла.

Аналогичным образом с помощью теории размерности можно получить и другие числа подобия для гидродинамических процессов.

5. РОЛЬ ЧИСЕЛ ПОДОБИЯ

Интересно установить абсолютное значение чисел подобия и области их изменения в практических задачах техники.

Число Re, характеризующее отношение сил инерции к силам вязкости, может быть представлено в виде

.

Если за линейный размер для корабля брать длину корабля и для самолета - хорду крыла, то числа Re и в этом и в другом случае изменяются в пределах 10⁵ - 10⁹. В гидротурбинах за характерный линейный размер обычно берут диаметр рабочего колеса. Тогда число Re для турбин изменяется в пределах 10⁴ - 10⁶.

Подобие поверхностных сил давления определяется равенством чисел М и k или при малых скоростях потоков - числом Эйлера. Если скорость звука

,

где m - молекулярный вес,

то число М будет иметь вид

.

Из формулы видно, что при одной и той же скорости движения и мало меняющихся k и g значение числа М пропорционально корню квадратному из величины молекулярного веса среды и обратно пропорционально корню квадратному из абсолютной температуры.

Современные самолеты летают при значениях чисел М = 0,2 - 1,0 и более, снаряды при М = 2 - 4 и ракеты при М = 5 - 8 и более. В проточной части турбомашин обычно число М < 1, т.е. потоки дозвуковые, и лишь в некоторых особых случаях имеют место потоки при М > 1.

Число Эйлера Eu характеризует отношение нормальных поверхностных сил давления к силам инерции и равно отношению перепада давлений в двух точках потока к скоростному напору.

В большинстве задач гидродинамики (внешнее обтекание тел, движение жидкостей и газа в трубах и др.) величина давления и скорости в любой точке потока однозначно определяется числом Re. Следовательно, Eu в этих случаях не является критерием подобия, и его значение полностью зависит от других чисел подобия. Например, при движении жидкости в трубах число Eu выражает безразмерную величину сопротивления и зависит лишь от числа Re

.

В некоторых задачах величина перепада задана и не связана однозначно с величиной скоростного напора в любой точке потока. В таких потоках число Еu не зависит от других чисел подобия и является критерием, соблюдение которого обязательно. Примером потока, при моделировании которого числа Еu должны быть строго одинаковы, является поток в проточной части любой турбомашины и, в частности, гидравлической турбины. В последнем случае величина перепада задана разностью уровней воды в верхнем и нижнем бьефе, и скорость в любой точке потока зависит не только от числа Re, но и от числа Еu.

Число Струхаля Sh характеризует составляющие инерционных сил, зависящих от времени. При этом может быть два случая:

1) когда нестационарность движения задается граничными условиями (машущее крыло, винт, колесо турбины и пр.);

2) когда нестационарность может являться следствием стационарного обтекания какого-либо тела, т.е. движение будет нестационарным по своей внутренней сущности.

В первом случае число Sh полностью определяется заданными условиями. Так, при исследовании работы винтов за характерное время принимается время одного оборота, т.е. период , за характерный линейный размер - диаметр винта D и тогда число Sh определяет величину, называемую относительной поступью

.

Для судовых винтов изменяется в пределах 0,3 - 3. Во втором случае число Sh является следствием подобия, т.е. число Sh есть функция числа Re. Так, при стационарном обтекании цилиндра с его поверхности периодически отрываются вихри, частота отрыва которых заранее неизвестна и определяется режимом обтекания, т.е. числом Re.

Число , в отличие от других чисел подобия, явно не зависит от параметров потока. Оно полностью определяется физическими свойствами газов, и зависимость его величины от параметров газа довольно сложна. При некоторых упрощениях можно считать, что величина зависит от числа атомов в молекуле. Для одноатомных газов k = 1,66, двухатомных k = 1,4, трехатомных k = 1,27; для молекулы с бесконечным числом атомов k стремится к единице.

Величина k слабо зависит от температуры. Так, для воздуха при изменении температуры от 0 до 1500 ⁰С она убывает от 1,4 до 1,28. Действительные значения показателя изэнтропы для различных газов в зависимости от температуры можно найти в термодинамических таблицах. Влияние величины числа k на обтекание существенно лишь при числах М значительно больших единицы.

Для полного моделирования необходимо полное подобие процессов, т.е. равенство чисел подобия. Но обычно пользуются приближенным моделированием, при котором подобие сохраняется по числам, наиболее характерным для данного процесса. Так, например, при стационарных процессах числа Sh не имеют значения. При изучении движения жидкости в трубе самым существенным числом будет число Рейнольдса. При испытании моделей турбомашин (турбины, насосы, компрессоры) необходимо равенство чисел Sh и Еu.

Число Re приобретает решающее значение при определении структуры потока. Все потоки делятся на ламинарные и турбулентные. Структура потока определяет процесс переноса массы, количества движения и тепла.

Выясним, как величина чисел подобия влияет на сопротивление тел. Сопротивление любого тела Х можно представить в виде

,

где - безразмерный коэффициент сопротивления;

S - характерная площадь.

Зависимость от числа Re для шара показана на рис. 1.

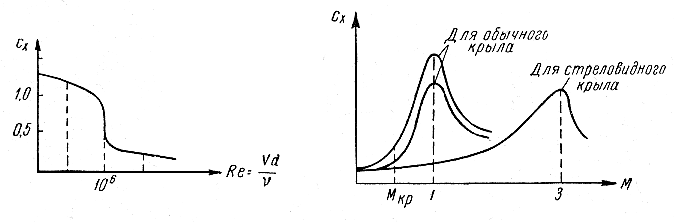
Рис. 1. Зависимость коэффициента сопротивления

от числа Рейнольдса Re

Из рис. 1 видно, что число Re существенно влияет на коэффициент сопротивления шара. Аналогичные кривые будут иметь место и для других плохо обтекаемых тел. Число Re, при котором происходит резкое падение сопротивления, называется критическим числом Рейнольдса и обозначается .

Число М также существенно влияет на сопротивление и другие аэродинамические характеристики. Для обычных самолетов существует так называемый «звуковой барьер». Он заключается в том, что при приближении скорости самолета к скорости звука коэффициент лобового сопротивления, как это видно из рис. 2, резко возрастает и дальнейшее увеличение скорости сопряжено с необходимостью значительного увеличения мощности двигателя.

Рис. 2. Зависимость коэффициента сопротивления

от числа Маха М

Число М, при котором где-либо вблизи обтекаемого тела скорость газа достигает местной скорости звука, что приводит к резкому увеличению сопротивления, называется критическим числом М и обозначается М_кр,. Значение М_кр для крыла меняется в пределах 0,7 - 0,8. Для уменьшения сопротивления строят самолеты со стреловидным крылом. При этом М_кр возрастает до 1,5 - 2,0 и несколько больше.

6. ТЕПЛОВОЕ ПОДОБИЕ

Аналогично гидродинамическому подобию рассмотрим условия теплового подобия. Вначале разберем случай чистой теплопроводности, т.е. переноса тепла молекулярным способом без конвекции. В этом случае уравнение переноса тепла имеет вид

,

где - удельная теплоемкость жидкости.

Напишем это уравнение в безразмерном виде, для чего введем следующие безразмерные величины:

,

где - безразмерные величины;

- характерные размерные величины (масштабы).

Рассмотрим одномерное движение, т.е. , тогда

.

Подставив выражения входящих в уравнение величин через их безразмерные значения и масштабы, получим

или

.

Как было указано ранее, называется коэффициентом температуропроводности.

Число, равное , называется числом Фурье. Оно характеризует нестационарность процесса молекулярного переноса.

Далее рассмотрим случаи конвективного переноса тепла. Для одномерного установившегося движения получим

.

Введя безразмерные величины, получим

,

или

.

Следовательно, для подобия необходимо соблюдать одинаковость значения , величины, характеризующей конвективный перенос; обратная величина называется числом Пекле (Ре)

.

Перенос тепла с поверхности при разности температур в потоке и на стенке , можно представить в виде

,

где - температура окружающей среды;

- температура стенки;

- коэффициент теплоотдачи (теплопереноса).

Для плотности тока имеем

.

Воспользуемся выражением (X. 16) и получим еще одно число подобия. Если уравнение в безразмерном виде

поделим на , то получим

.

Число называется числом Нуссельта и обозначается

.

Так как коэффициент теплоотдачи , входящий в число Nu, меняется от точки к точке, то такое число Nu является локальным.

Если в выражение для числа Nu подставить среднее значение коэффициента

,

то полученное значение будет называться средним значением числа Нуссельта.

Количество тепла, которое снимается со стенки, имеющей длину l и ширину, равную 1, будет

.

Физически число Nu можно рассматривать как отношение действительного потока, определяемого величиной коэффициента теплоотдачи , к удельному тепловому потоку, который имел бы место в условиях чистой теплопроводности в слое толщиной l, т.е.

.

Если разделим число Ре на число Re, то получим число Рr, равное

.

Число Pr характеризует отношение двух характеристик молекулярного переноса: кинематической вязкости v и коэффициента температуропроводности а. Перенос импульса, связанный с величиной v, определяется разностью скоростей, а перенос тепла, связанный с величиной а, разностью температур. Следовательно, число Pr, явно содержащее лишь величины, определяющие физические свойства среды, в действительности характеризует отношение между полями скоростей и температур.

Тогда зависимость

можно трактовать следующим образом: количество переносимого тепла (Nu) зависит от вида скоростного поля (Re) и его связи с полем температур (Pr).

Для идеальных газов число Pr, однозначно определяемое числом атомов в молекуле и независящее от температуры и давления, приведено в табл. X. 1.

Для реальных газов число Pr зависит от температуры и давления и определяется экспериментально. Для газов число Pr немного меньше единицы, для жидкостей - всегда больше единицы и может достигать больших значений (масла). Для жидких металлов и ртути число Pr имеет очень малые величины.

Таблица X. 1

Число атомов		Pr
1	1,66	0,67
2	1,40	0,73
3	1,30	0,80
4 и более	-	1,00

Числа Pr для некоторых сред приведены в табл. X. 2.

Число Pr для жидких металлов в зависимости от температуры показано на рис. X. 4.

Таблица X. 2

Среда	Температура, °С
	20	60	100	400
Воздух	0,7	-	0,690	0,661
Вода	7,02	3,02	1,74	-
Масло	10400	1050	276	-
Ртуть	0,0249	-	0,0162	-
Водяной пар	-	-	1,12	0,876

Рис. Х.4. Числа Pr для жидких металлов

Очевидно, что малые значения числа Ре соответствуют очень малому конвективному переносу в общем переносе тепла. Следовательно, при значениях чисел Ре << 1 наблюдается только молекулярный перенос, т.е. теплопроводность; в то время, как при больших значениях числа Ре роль молекулярного переноса будет ничтожна.

Так как

,

то для газов, для которых обычно число Pr = 0,7 - 0,9, можно считать

.

Последнее означает, что большим числам Ре будут соответствовать большие числа Re, а следовательно, при некотором достаточно большом числе Re перенос тепла будет осуществляться путем турбулентной конвекции.

При турбулентном течении жидких металлов отношение потока тепла, переносимого молекулярной теплопроводностью, к потоку тепла, переносимому за счет турбулентного перемешивания, может быть приблизительно оценено следующим образом.

При значениях

преобладает механизм передачи тепла молекулярной теплопроводностью. При числах Ре порядка 1000 роль молекулярного и турбулентного механизмов переноса приблизительно одинакова, и лишь при Ре > 50000, т.е. при очень высоких скоростях течения, в ядре потока преобладает турбулентный перенос тепла.

7. ДИФФУЗИОННОЕ ПОДОБИЕ

Числа подобия для диффузионных процессов можно легко получить из уравнения диффузии вещества. Для одномерного движения уравнение молекулярной диффузии будет иметь вид

.

Подставим в уравнение выражения входящих в него величин через безразмерные и характерные значения (масштабы):

или .

Безразмерное число называется диффузионным числом Фурье. Очевидно, что оно аналогично тепловому числу Фурье. При конвективном переносе вещества для одномерного движения воспользуемся уравнением

.

Проделав аналогичные преобразования, получим

.

Число называется диффузионным числом Пекле.

Число соответствует числу Re, определяющему структуру потока, и по тому, велико ли число по сравнению с единицей или мало, можно судить о том или ином характере режима переноса вещества. В первом случае молекулярной диффузией можно пренебречь по сравнению с конвективным переносом вещества, во втором - наоборот, молекулярная диффузия является определяющей.

Поделив число Ре на число Re, получим диффузионное число Прандтля , равное отношению кинематической вязкости к коэффициенту диффузии

.

Во многих работах число называется числом Шмидта. Напишем теперь уравнение переноса вещества, отнесенное к разности концентраций на стенке и в окружающей среде

,

где коэффициент переноса массы;

концентрация в окружающей среде;

концентрация на стенке.

Запишем это уравнение в безразмерном виде

или

.

Тогда получим локальное число равное

.

Аналогично тепловому числу Nu можно, воспользовавшись средним коэффициентом переноса вещества , ввести среднее диффузионное число Нуссельта.

В газах числовое значение коэффициентов диффузии и вязкости имеет один порядок, поэтому .

Иначе обстоит дело в жидкостях. Коэффициент кинематической вязкости подвижных жидкостей типа воды составляет около . Коэффициент диффузии молекул и ионов в водных растворах имеет порядок , у макромолекул - . Поэтому в воде и сходных жидкостях будет . При возрастании вязкости коэффициент диффузии уменьшается по закону

,

поэтому число растет с увеличением вязкости, пропорционально квадрату последней. В вязких жидкостях число достигает значения 10⁶ и более. Для жидких металлов число значительно меньше единицы. Значения для некоторых сред приведены в табл. X. 3.

Таблица X. 3

Диффунди-рующее вещество	Среда, в которой происходит диффузия	Температура °С	D м2/с
Hg	N2	19	3,2510-3	0,00424
СО2	Н2	18	6,0510-5	0,158
NН3	Воздух	0	2,1710-5	0,634
О2	N2	12	2,0310-5	0,681
НС1	Н2О	0	2,2310-6	0,81
С6Н6	Воздух	0	7,510-6	1,83
С6Н6	Н2	0	2,9410-5	3,26

Следует отметить, что для газов тепловое и диффузионное числа Pr имеют одинаковый порядок, поэтому процессы переноса тепла и вещества в газах аналогичны, но процессы переноса тепла и вещества в жидкостях сильно отличаются друг от друга, так как сильно отличаются числа Pr и .

Можно заметить сходство между некоторыми числами подобия. Так, число Re похоже на числа Пекле тепловое и диффузионное. Исходя из этой аналогии, эти числа можно было бы назвать числами Рейнольдса - динамическим, тепловым и диффузионным, т.е.

; и .

Тогда в соответствии с ранее введенным определением имеем

и .

Эта аналогия используется и в электромагнитной гидродинамике (см. гл. XV), где вводятся магнитное и электрическое числа Рейнольдса.

10. ПЛОСКОЕ ТЕЧЕНИЕ МЕЖДУ ПЛАСТИНКАМИ

Приближенные методы решения для потоков при малых числах Re нами подробно не рассматриваются, поэтому в качестве примера приведем задачу о потоке между двумя очень близко расположенными пластинками.

Если обозначить малое расстояние между пластинками h и считать, что число очень мало, т.е. инерционные силы малы по сравнению с силами вязкости, то в уравнениях Навье - Стокса (X. 7.) можно пренебречь силами инерции и отбросить левую часть их. Тогда при отсутствии массовых сил система уравнений примет вид

; ; .

Пусть уравнения плоскостей, между которыми течет жидкость, будут

и ,

тогда, имея ввиду малость величины h, будем считать, что и что изменение u и по z будет сильнее, чем по х и у. Последнее означает, что

или ;

или ,

и соответственно

и и т. д.

Тогда, используя эти соотношения, получим уравнения (X. 17) в виде

; ; .

Так как из третьего уравнения видно, что давление не зависит от координаты z, то интегралы первого и второго уравнений будут

;

.

Для нахождения А, В, А₁ и В₁ воспользуемся следующими граничными условиями: при z = 0 и z = h .

Учитывая эти условия, найдем u и

;

.

Подставим найденные значения в уравнение неразрывности

,

получим

.

Из равенства (X. 20) видно, что давление в рассматриваемом движении жидкости есть гармоническая функция.

Введем средние значения скоростей

; .

Подставляя выражения (X. 19) в формулы (X. 21) и имея ввиду, что

,

получим

и

.

Если теперь введем функцию

,

то она будет потенциалом средних скоростей, так как

и .

Тогда по равенству (X. 20) потенциал будет удовлетворять уравнению Лапласа

.

Следовательно, средние скорости при движении вязкой жидкости с малым числом Re между двумя пластинами соответствуют скоростям потенциального потока. Последние соотношения используются для так называемой ламинарной аналогии потенциального потока (см. п. 2, гл. XVI).

9.1. Понятие о методе размерностей. Пи-теорема

9.2. Числа и критерии подобия

9.3. Методы моделирования

9.4. Методы аналогий

10. Общее уравнение энергии в интегральной и дифференциальной формах

11. Турбулентность и ее основные статистические характеристики

11.1. Осредненные параметры и пульсации

11.2. Стандарт пульсационной скорости и степень турбулентности

11.3. Двухслойная модель турбулентности

189