5.5. Примеры аналитических решений уравнений Навье-

Стокса для ламинарного движения в цилиндрических трубах

В качестве первого примера интегрирования уравнения Стокса рассмотрим ламинарное стабилизованное движение несжимаемой жидкости в круглой цилиндрической трубе.

Под стабилизованным движением будем понимать такое стационарное движение, при котором скорость потока и профиль скоростей не зависят от продольной координаты. Следовательно, если направление движения совпадает с осью х, то проекции скоростей на оси у и z будут равны нулю, а проекция скорости на ось х будет зависеть только от у и z. Такое движение будет иметь место на плоской стенке или в цилиндрической трубе на значительном расстоянии от входа.

Если направление потока в трубе произвольного сечения совместить с осью х и считать, что для стабилизованного движения составляющие скоростей и отсутствуют, то в общем случае будем иметь

и .

Используя уравнение неразрывности движения, получим, что ди / дх = 0 и, следовательно, скорость в трубе не зависит от координаты х. Последнее является условием для стабилизованного движения.

Уравнение Стокса после подстановки значений , и и пренебрежения массовыми силами будет иметь вид

;

и .

Из последних уравнений следует: 1) величина давления не зависит от поперечных координат у и z и есть функция только координаты х, т.е., в частности, в круглой трубе давление меняется только вдоль оси, а следовательно, постоянно в каждом сечении и не зависит от радиуса; 2) так как левая часть первого уравнения зависит только от у и z, а правая часть не зависит ни от у, ни от z, то, следовательно, и правая и левая части этого уравнения должны быть равны одной и той же постоянной величине, т.е.

dp / dx = const. (5.47)

Таким образом, уравнение Стокса для стабилизованного движения жидкости в цилиндрической трубе произвольного сечения или в более общем случае для прямолинейно параллельного стабилизованного движения вдоль оси х будет иметь вид

. (5.48)

Если прямоугольную систему координат заменить на цилиндрическую, в которой и , то уравнение (5.48) в цилиндрической системе координат будет

. (5.49)

Вид решения уравнений (5.48) или (5.49) определяется граничными условиями, задаваемыми формой поперечного сечения трубы. Для трубы круглого поперечного сечения, ось которой совпадает с осью х, естественно пользоваться уравнением в цилиндрической системе координат (5.49).

Предполагая, что поток обладает осевой симметрией

,

получим уравнение (5.49) в виде

(5.50)

Так как

,

то уравнение (5.50) окончательно примет следующий вид

. (5.51)

После последовательного двойного интегрирования получим общее решение уравнения (5.51)

. (5.52)

Произвольные постоянные и определяются из граничных условий. Для круглой трубы с радиусом они могут быть записаны так: при , а при r = 0 u - конечная величина.

Подставив r = 0 в уравнение (5.52), получим при бесконечное значение скорости на оси. Следовательно, для удовлетворения второго граничного условия необходимо положить .

Используя первое граничное условие, найдем

.

Таким образом, для круглой трубы распределение скоростей по сечению будет параболическим, т.е.

. (5.53)

По уравнению (5.47) можно написать

, (5.54)

где - перепад давления в трубе длиной l.

Определим среднюю расходную и максимальную скорости в круглой трубе. Объемный расход Q

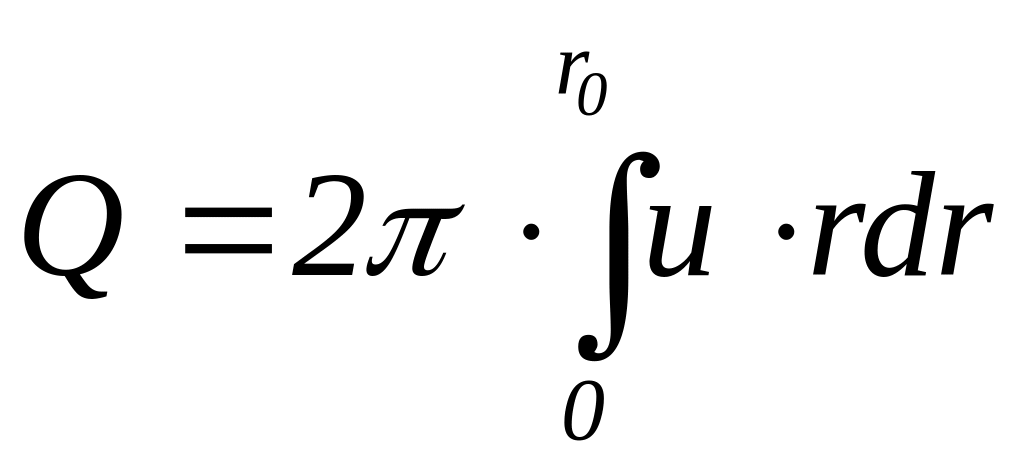(5.55)

или, подставляя u из формулы (5.53) и используя выражение (5.54), получим

. (5.56)

Формула (5.56) выражает известный закон о том, что секундный объемный расход жидкости при установившемся ламинарном движении несжимаемой жидкости в цилиндрической трубе круглого сечения пропорционален перепаду давления на единицу длины трубы и четвертой степени ее радиуса (или диаметра). Этот закон часто называется законом Пуазей-ля, исследовавшего законы движения крови по капиллярным сосудам.

Величина средней расходной скорости , будет

. (5.57)

Наибольшее значение скорости , как видно из выражения (5.53), будет на оси трубы, т.е. при r = 0, и равно

. (5.58)

Из сравнения двух последних формул получим очень важное свойство ламинарного установившегося движения жидкости в круглой трубе: максимальная скорость на оси трубы в два раза больше средней расходной скорости, т.е.

. (5.59)

Это свойство можно использовать при нахождении объемного расхода, определяя не весь профиль скоростей, что необходимо в соответствии с формулой (5.55), а лишь значение скорости на оси трубы. Тогда формула для расхода будет

.

Если отнести значение скорости в любой точке к максимальной скорости на оси трубы, то можно вместо выражения (5.53) получить безразмерный профиль скоростей

(5.60)

в виде параболоида вращения с меридианальным сечением в форме параболы.

Найдем величину сопротивления при движении жидкости в трубе. Для установившегося движения в цилиндрических трубах сопротивление на данном участке определяется перепадом давления на этом участке либо по формуле

, (5.61)

либо по формуле

, (5.62)

где и - коэффициенты сопротивления.

Приравнивая правые части равенств (5.61) и (5.62) и имея в виду, что , получим отношение между коэффициентами и в форме

. (5.63)

Определяя из формулы (5.57) и приравнивая полученное значение правой части (5.61), найдем

,

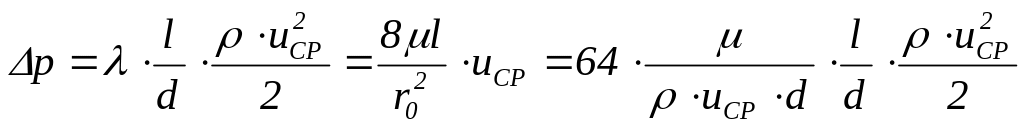откуда следует, что величина коэффициента сопротивления Л

, (5.64)

где - число Рейнольдса, составленное по расходной скорости и диаметру трубы d.

Выражение коэффициентов сопротивления как функций числа Рейнольдса или называется законом сопротивления ламинарного движения вязкой жидкости в цилиндрической трубе. Зная или , легко найти перепад давления по выражениям (5.61) и (5.62), а следовательно, и величину мощности, необходимой для перекачки заданного расхода Q (м³ / с). Формула мощности имеет вид

.

Для решения задачи о продольном движении жидкости между двумя соосными цилиндрами с радиусами и постоянные и в уравнении (5.52) определим, исходя из следующих граничных условий: величина скорости на стенках цилиндров равна нулю, т.е. при и .

Тогда, считая получим формулу распределения скоростей

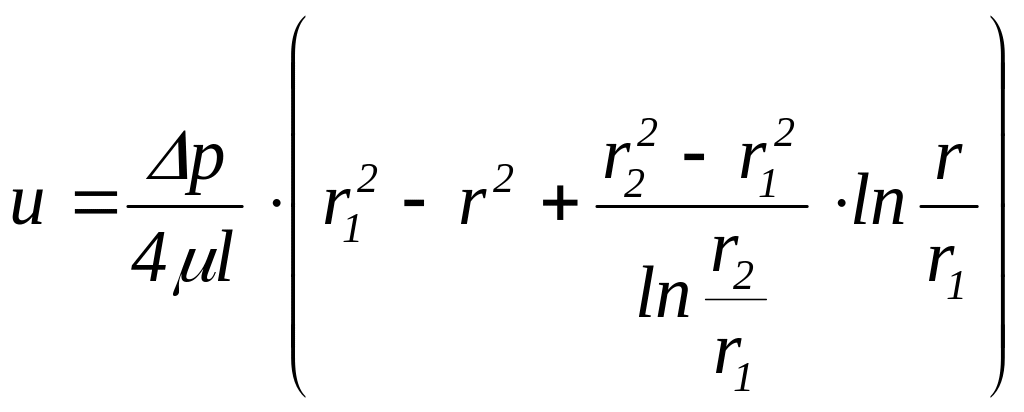. (5.65)

Величину расхода и средней скорости найдем в виде

;

,

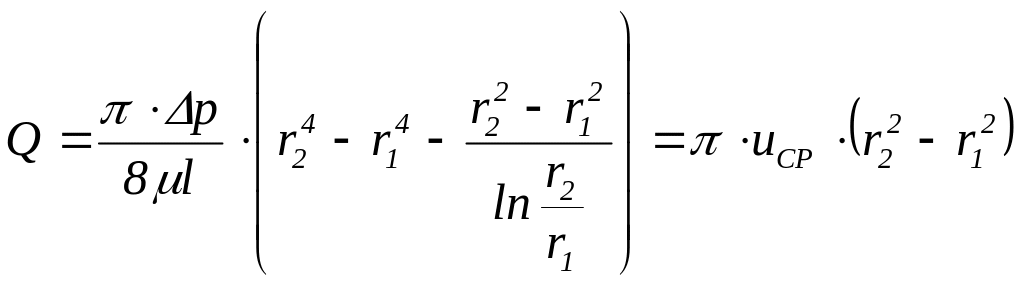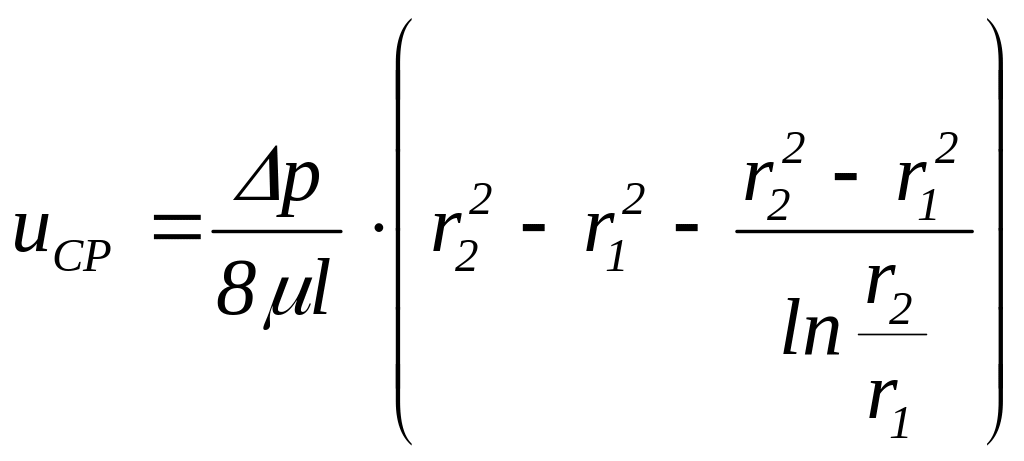откуда величина перепада давления будет

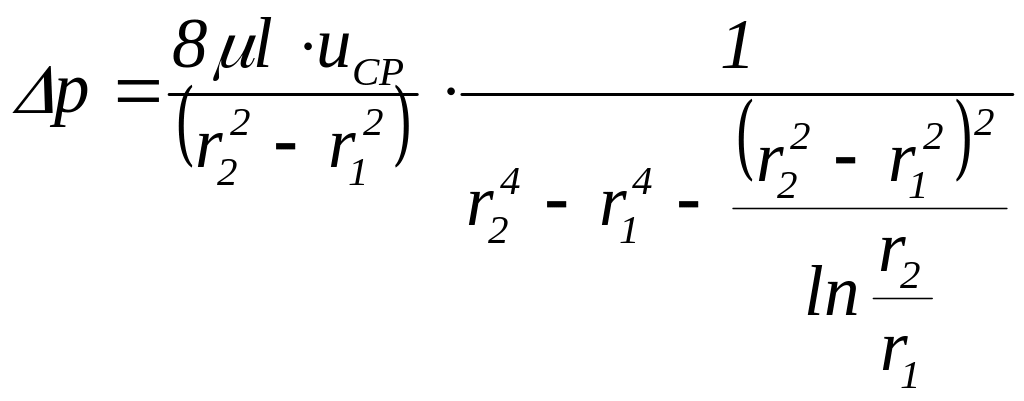. (5.66)

Для очень узких кольцевых щелей, т.е. при малой разности радиусов, допустимо щель считать ограниченной параллельными плоскостями. Тогда формула (5.66) значительно упрощается и принимает вид, очень удобный для практических расчетов

, (5.67)

где - ширина щели.

Принимая для потока между соосными трубами выражение перепада давления по формуле

,

получим из выражения (5.67) закон сопротивления для ламинарного движения в щели между соосными цилиндрами

,

где .

Существует также точное решение для щели, образованной не концентрическими цилиндрами. Не рассматривая здесь довольно громоздких решений, приведем лишь приближенную формулу для сопротивления при цилиндрах с мало отличающимися радиусами

,

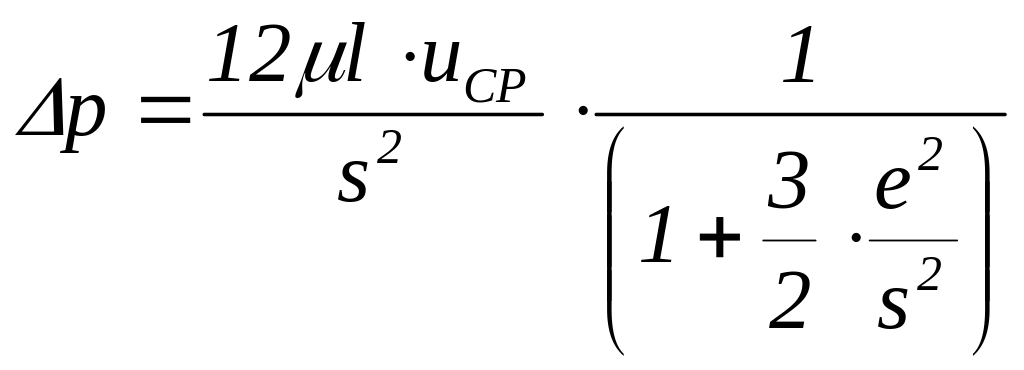где e - эксцентриситет;

s - ширина щели, которая была бы при отсутствии эксцентриситета.

Результаты многочисленных опытов при ламинарном установившемся движении в трубах круглого и кольцевого поперечного сечения хорошо совпадают с соответствующими данными, полученными по вышеприведенным формулам.

Уравнение (5.58) было решено и для труб с эллиптическим, прямоугольным и треугольным поперечными сечениями. Приведем без доказательства некоторые формулы для ламинарного стабилизованного движения в трубах эллиптического сечения.

Если а и b будут полуоси эллипса, а контур трубы в плоскости yz представить в виде , то распределение скоростей в сечении трубы

(5.68)

дает уравнение поверхности эллиптического параболоида, а изотахи (линии равных скоростей) - подобные друг другу эллипсы, т.е. эллипсы с одинаковыми отношениями полуосей.

Из уравнения (5.68) видно, что скорость будет максимальной на оси трубы, т.е. при у = z = 0, и она равна

.

Зная можно скорость по формуле (5.68) представить в безразмерном виде

.

Величина объемного расхода через трубу эллиптического сечения легко определяется интегрированием скорости (5.68) по сечению, т.е.

.

После вычисления интеграла получим

.

Разделив объемный расход на площадь поперечного сечения трубы , определим среднюю величину скорости

.

Следовательно, так же как и для круглой трубы средняя скорость равна половине максимальной.

Из последней зависимости можно найти выражение для сопротивления и, используя выражение (5.61), получить закон сопротивления.

Легко видеть, что все формулы, полученные для трубы эллиптического сечения при а = b переходят в соответствующие зависимости для круглой трубы.