1. Кинематические характеристики поступательного движения.

Кинематика отвечает на вопрос, где находится материальная точка, каковы её скорость и ускорение. При этом используется система отсчёта представляющая собой совокупность: тело отсчёта, система координат и часы отсчитывающие время. В самом лучшем случае используется - декартова система координат. Каждой оси направлен единичный вектор направления OX-i,OY- j,OZ - k. Все они взаимно перпендикулярны и равны 1. Вектор r - радиус вектор материальной точки М, то есть вектор проведённый из начала координат к точке М.

r = x i + y j + z k.

Быстрота изменения (r) во времени характеризуется (v), которая представляет собой производную (r) по (t).

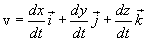
В большинстве задач считается, что орты постоянны во времени, а значит их производные по времени = 0.

Быстроту изменения скорости по времени характеризует ускорение.

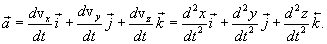
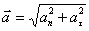Ускорение так же можно представить в виде суммы двух ускорений тангенсального и нормального.

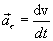Тангенсальное ускорение характеризует изменение скорости по модулю.

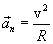Нормальное ускорение характеризует изменение скорости по направлению.

2.Движение по окружности.

Траектория большинства точек тела при вращательном движении окружность. При таком расположении оси вращения точка окружности (центр начала координат, который лежит на оси вращения) расположены в плоскости перпендикулярной поверхности чертежа. В этом случае окружность изображается в виде овала или элипса.

Положение мат. точки на траектории указывает псевдовектор угла поворота и вектор. Псевдовектор угла поворота (φ) равен по модулю углу (φ) в радианах, а его направление связано с направлением вращения правилом правого винта. Если с конца (φ) смотреть на вращение мат.точки по окружности, то оно будет видно происходящим против часовой стрелки.

Быстроту изменения вектора угла поворота характеризует угловая скорость

Угловая скорость связана с линейной [ ]

При равномерном вращении = const. в этом случае рассматривают период и частоту обращения.

Период (T) - время одного полного поворота

Частота (ν) - число оборотов в единицу времени ,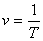

Быстроту изменения угловой скорости по времени характеризует угловое ускорение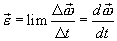

Угловое ускорение связано с тангенсальным ускорением

[ ]

3.Криволинейное движение.

Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением где r – радиус окружности.  Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.  Ускорение также можно разложить на тангенциальное (dU/dt) и нормальное (V²/R).Важнейшими характеристиками равномерного движения по окружности являются период и частота обращения. При равномерном вращении 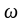=const в этом случае рассматривают период и частоту вращения; Т – это время одного полного оборота Т = 2 / . Частота n-это число оборотов в единицу времени n=1/t ; =2 n При неизменной частоте обращения центростремительное ускорение прямо пропорционально расстоянию от движущейся частицы до центра вращения.

4.Законы Ньютона.

Первый закон Ньютона: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние. Свойство материальных объектов сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Мерой инертности материального объекта при поступательном движении является его масса. Системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными системами отсчета. Строго инерциальных систем отсчёта нет. Неинерциальные системы отсчёта движутся относительно инерциальных с ускорением.

Второй закон Ньютона: Ускорение с которым движется мат. точка прямо пропорционально равнодействующей всех действующих сил и обратно пропорциональна её массе. 2. З-н. является основным законом динамики поступательного движения, у него есть более общая форма записи. В механике Ньютона масса считается постоянной величиной, поэтому её можно вынести из под знака производной. - более общая форма записи второго закона.

Произведение импульса мат.точек по времени равна равнодействующей всех действующих на неё сил.

Третий закон Ньютона: Две мат. точки действуют друг на друга с равными по значению и обратными по направлению силами и приложены к разным точкам. Из 3 закона следует что силы возникают попарно.

5.Принцип независимости действия сил.

Для упрощения нахождения равнодействующей всех сил действующих на мат.точку в механике используется принцип независимости действия сил (суперпозиция).

Если на мат.точку действуют одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение независимо от наличия и действия других сил. По закону Ньютона можно записать: F=ma  F_i=m_ia_i Масса явл. постоянной величиной и может быть вынесена за знак суммы: а = аi