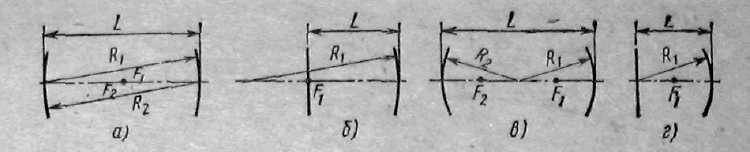
3. Резонатори з довільними сферичними дзеркалами.

Це резонатори, що складаються з двох співвісних сферичних дзеркал радіусами R1 і R2, розташованих на відстані, L один від одного. Властивості таких резонаторів легко визначити, якщо знайдена відповідна конфокальная система, в якій дві синфазні поверхні співпадають з поверхнями дзеркал резонатора.

Якщо відомі радіуси R1 і R2 дзеркал і відстань між ними, то з виразу (3) можна знайти довжину, а також радіуси кривизни і координати дзеркал еквівалентного конфокального резонатора.

Якщо відоме Lек, то розподіл поля всередині і поза резонатором буде таким же, як в еквівалентному конфокальном резонаторі. Зокрема, радіус світлової плями визначатиметься співвідношенням (4), де замість L стоятиме Lек.

Якщо резонатор утворений двома однаковими сферичними дзеркалами радіусами R1=R2=R, розташованими на відстані L один від одного, то з (3) отримуємо, що довжина еквівалентного конфокального резонатора

(5)

Еквівалентний конфокальний резонатор визначає тільки власні функції довільного сферичного резонатора.

Сферичний резонатор може бути або стійким (промінь заишається в межах обмеженої області) або нестійким (коли промінь послідовно відображається від кожного з дзеркал, віддаляється на необмежено велику відстань від осі резонатора)

(у останньому випадку резонатор по суті втрачає свої резонансні властивості).

Умова стійкості резонатора:

0<g1g2<1, (*)

Де g1g2 – радіуси кривизни.

Умова * виражає умову при якій в даном резонаторі можливо спостерігати стійку моду ТЕМ_00.

Також існують нестійкі резонатори, які підрозділяються на 2 класи:

1. коли g1g2 >1, резонатори додатної гілки,

2. коли g1g2 <0, резонатори від’ємної гілки.

На рис.1 приведена діаграма, що ілюструє умову стійкості оптичних резонаторів. Стійкі області відповідають заштрихованим ділянкам.

Т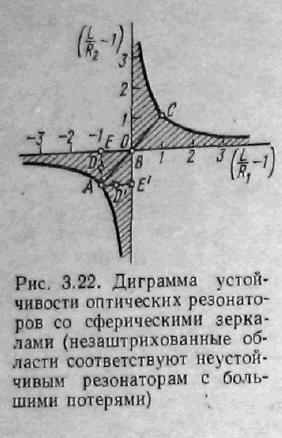 очці А (-1; -1) відповідає резонатори з плоскими дзеркалами, розташований на межі стійкості.

Точці В (0; 0) відповідає конфокальний резонатор.

Точці С (1; 1) відповідає резонатор, утворений двома однаковими сферичними дзеркалами, осі і центри кривизни яких співпадають, тобто R1=R2=L/2.

Такий концентричний резонатор також лежить на межі, що розділяє стійка і нестійка області. Дифракційні втрати в ньому дуже швидко зростають із збільшенням типу коливань, тобто із збільшенням індексів m n. Тому такий резонатор використовують для селекції (відбору) неаксіальних коливань: за рахунок великої різниці в дифракційних втратах між аксіальними ТЕМ₀₀ і неаксіальними модами останні в концентричному резонаторі володіють малою добротністю і, отже, гасяться.

Т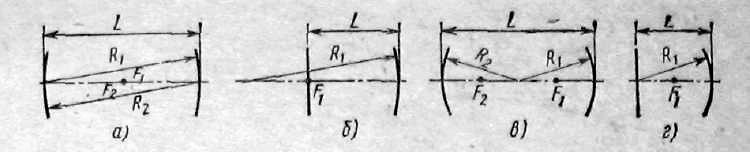 очкам D D' (-1; -0,5) і (-0,5; -1) відповідає полуконфокальний резонатор, тобто резонатор, утворений одним плоским і одним сферичним дзеркалом, радіус кривизни якого рівний подвоєній довжині резонатора.

Він знаходиться в середині стійкої області і його властивості аналогічні конфокальному резонатору з подвоєною довжиною.

Т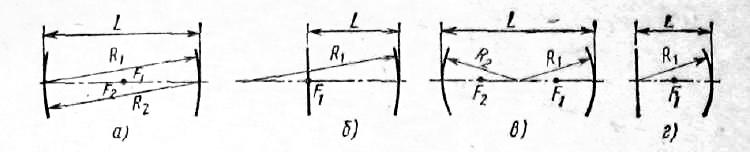 очкам В і Е' (-1; 0) і (0; -1) відповідає півконцентричний резонатор. Він володіє особливостями, характерними для концентричного резонатора, а також застосовується для селекції неаксіальних коливань.