112 Вектор-потенціал магнітного поля.

Електростатичне поле характеризується як напруженістю поля, так і потенціалом: 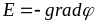. В магнетостатиці вектор напруженості магнітного поля також знаходять, застосовуючи диференціальний оператор до деякої функції, однак, ця функція є вектором та називається вектором-потенціалом магнітного поля і за звичай позначається . Зв’язок векторів і задається співвідношенням. . Перевіримо коректність такої заміни на рівняннях Максвелла: ,отже це рівняння Максвелла одразу ж задовольняється. Потенціал можна вибирати із точністю до константи. Замість будемо брати величину , де деяка скалярна функція. Накладемо додаткову умову (умова калібровки потенціала) . Тоді подивимось, що буде із другим рівнянням Максвелла 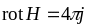; ; . Але , отже отримали рівняння, аналогічне рівнянню Пуассона в електростатиці 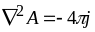. Тепер по аналогії з електростатикою : рівняння Пуассона , потенціал пов’язаний із густиною заряду співвідношенням 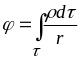. Особливість полягає у тому, що потенціал векторний, тому що магнітне поле не потенціальне. Остаточно маємо вираз для вектор-потенціалу . Таким чином, знаючи розподіл густини струму у просторі, можна знайти вектор , а відтак, і вектор напруженості магнітного поля . Вектор-потенціал має ще одну властивість. Нехай у магнітному полі вибрано деякий контур і натягнуто на нього довільну поверхню . Потік вектору через цю поверхню . Скористаємось формулою Стокса . Таким чином, потік вектору напруженості магнітного поля через поверхню, натягнуту на контур, дорівнює циркуляції вектор-потенціалу по цьому контуру. Це аналог закону повного струму 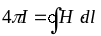, де роль потоку грає 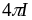( також потік, але вектору ), роль вектору грає вектор .

113 Квантові уявлення про природу феромагнетизму.

Вейсс у своїй класичній теорії показав, що якщо на магнетик діє зовнішнє поле , то на кожний магнітний момент діє молекулярне поле ,де стала Вейсса. Оцінки за класичною теорією і за експериментальними даними дали розбіжність у значенні сталої Вейсса у 3-4 порядки. Отже, запросимо на допомогу квантову теорію. Квантова теорія показує, що вираз для енергії взаємодії атомів та має вигляд , де спіни та атомів, а обмінний інтеграл, величина якого залежить від ступеня перекриття електронних оболонок та атомів. Модель феромагнетику, в якій виходять із виразу для енергії такого вигляду, називається моделлю Гейзенберга.

Розподіл заряду в системі із двох електронів залежить від взаємного розташування їх спінів, тобто від того, паралельні вони чи антипаралельні (можливо лише останнє - принцип Паулі). Різниця енергій, що відповідаєють паралельній і антипаралельній орієнтації спінів називається обмінною енергією. Знайдемо зв’язок між обмінним інтегралом 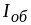і сталою Вейсса (яку в квантовій теорії іноді ще називають обмінною сталою). Нехай взаємодія виділеного атома з кожним із сусідів характеризується обмінним інтегралом . Обмінна енергія буде визначатись як енергія перевороту заданого спіна у присутності інших. Тоді , де 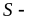середнє значення спіну в напрямку намагніченості. З іншого боку, різницю енергій паралельного і антипаралельного станів модна записати через середній магнітний момент електрона 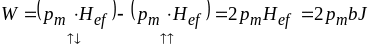. Скористаємось деякими позначеннями з теорії Вейсса, як то намагнічуваність насичення, середній спіновий магнітний момент електрона (у вільного електрона , , ). Тоді, прирівнявши вирази для енергій, маємо , звідки .

Поблизу точки Кюрі ми знаходимось між феромагнітним і парамагнітним станами. Врахування квантування енергії у теорії Ланжевена дало нам намагнічуваність, що при малих значеннях аргументу дорівнює .Оскільки молекулярне поле Вейсса пов’язане із вектором намагніченості як 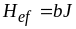, звідси .Два отриманих незалежно вирази для сталої Вейсса дають нам можливість визначити обмінний інтеграл .Тепер можна оцінити, що значення сталої Вейсса, виражене через обмінний інтеграл становить саме одиниці. З експериментальних даних для заліза еВ (або Дж); ; (СІ); 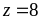(ОЦК гратка); 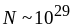м^-3. Тоді .
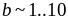