45. Рівняння неперервності та умова стаціонарності струму

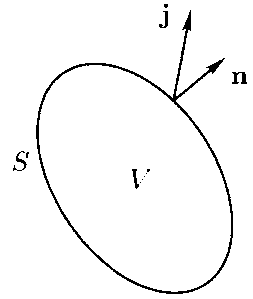
-густина заряду, - густина струму.Візьмемо в середовищі довільну замкнуту поверхню 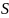, яка обмежує обєм V .Кількість струму, який щосекундно витікає з обєму через поверхню , представимо інтегралом . З іншого боку воно ж доріювнює . Отримали: , ,

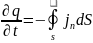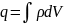Отже: 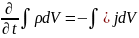. Так як це співвідношення має виконуватися для будьякого V тому .Якщо струми стаціонарні, тобто не залежть від часу, то ми отримаємо формули

46.Електричне поле в умовах протікання струму

Рух зарядів у провідниках відбувається під впливом сили, яка діє на ці заряди. Таким чином, існує електричне поле - поле постійних струмів . В цьому полі густина зарядів не залежить від часу, отже, воно є тотожним до поля нерухомих зарядів, які розподілені і закріплені у просторі за тим же законом, що і у випадку поля постійного струму. Отже, стаціонарне поле постійного струму, подібне до електростатичного поля, є потенціальним, і для нього виконуються співвідношення

; ; .

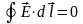(різниця між електростатичним полем і полем стаціонарного струму) Для електростатичного поля поверхня будь-якого провідника є еквіпотенціальною, вектор направлений вздовж нормалі до поверхні провідника, на якій існує поверхнева густина зарядів .

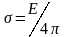У

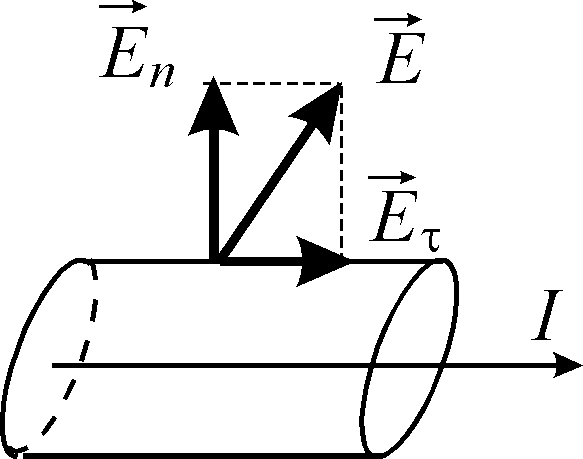
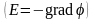випадку постійного струму поверхня провідника не є еквіпотенціальною, якщо вздовж провідника тече струм. Наявність різниці потенціалів вздовж поверхні означає наявність поля вздовж поверхні . Тому, на відміну від електростатики, вектор для постійного струму нахилений по відношенню до нормалі і має як нормальну 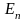, так і тангенціальну складову .

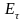Всередині провідника 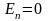, оскільки завдяки поверхні рух зарядів у провіднику в цьому напрямку неможливий. На поверхні міститься заряд, поверхнева густина якого . Ці поверхневі заряди змінюються вздовж поверхні, створюючи тангенціальну складову в просторі над провідником. Але оскільки 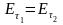, всередині провідника виникає електричне поле , яке приводить заряди в рух, створюючи струм.

Для підтримання постійного струму, тобто руху електронів із сталою швидкістю, потрібна неперервна дія сили, яка дорівнює 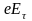( заряд електрона). А це означає, що електрони у провідниках рухаються із тертям. Інакше кажучи, провідники мають електричний опір.

47. Закон Ома в інтегральній і диференціальній формі.

(Інтегр ф) Для підтримки постійного струму, необхідна неперервна дія сили (F=e*Et, де e – заряд електрона, Et – складова напруженості поля , що напрямлена вздовж провідника). Це означає, що електрони в провідниках рухаються із тертям, або, інакше кажучи, що провідникам властивий електричний опір. Для кожного провідника існує однозначна залежність між напругою U, прикладеною до кінців провідника та силою струму i в ньому. Для багатьох провідників ця залежність проста і виражається формулою 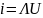(закон Ома), де 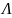– електропровідність провідника. Величина, обернена до електропровідності називається електричним опором(позначається R). .

(Диф ф) Закон Ома в інтегральній формі дозволяє знайти силу струму у тих випадках, коли трубки струму є циліндрами постійного перерізу, але часто це не так(напр. сферичний конденсатор). Розглянемо в однорідному та ізотропному провідному середовищі невеликий відрізок трубки струму довжини Δl і два близьких її еквіпотенціальних перерізи 1 і 2. Позначимо їх потенціали через U1 і U2, а середню величину площі перерізів – через ΔS. За законом Ома отримаємо: 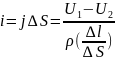, - питомий опір. , де λ = 1/ = питома електропровідність. Здійснивши граничний перехід, отримаємо: 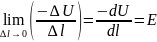, де E – напруженість електричного поля всередині провідника. Оскільки j та E – вектори, і що всередині ізотропних середовищ вони напрямлені однаково, то – закон Ома в диференціальній формі.