15.Скалярное произведение векторов и его свойства.Условие перпендикулярности векторов.Угол между векторами.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла фи между ними

Скалярное произведение равно сумме произведений соответствующих координат этих векторов.

Скалярный квадрат вектора равен квадрату его длины.

свойства проекций:

1)     Равные векторы имеют равные проекции на одну и ту же ось.

2)     пр пр пр .

3)     пр пр , .

4)     пр , где  – угол между вектором и осью.

Заметим, что проекция вектора на ось и его составляющая связаны соотношением сост пр .

Условие перпендикулярности векторов

• Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.

• Даны два вектора a (xa;ya) и b (xb;yb). Эти векторы будут перпендикулярны, если выражение x_ax_b + y_ay_b = 0.

Углом между двумя ненулевыми векторами  и  называется наименьший угол ( ), на который надо повернуть один из векторов до его совпадения со вторым. Предварительно нужно привести векторы к общему началу О (рис. 7).

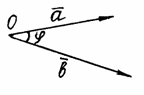
Рис. 7

Под углом между вектором  и осью  понимают угол между векторами  и  (рис. 8).

 

16.Векторное произведение и его свойства.

Упорядоченная тройка некомпланарных векторов называется правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае тройка называется левой (начала векторов тройки предполагаются совмещенными).Так, на рис. 16 тройка , ,  – правая, а тройка , , – левая (из конца вектора  кратчайший поворот от  к  виден по часовой стрелке).

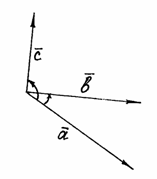
Рис. 16Векторным произведением двух векторов называется вектор, который обозначается  или и определяется следующим образом: 1)     где  – длина этого вектора равна произведению длин перемножаемых векторов на синус угла между ними; 2)      , – этот вектор перпендикулярен каждому из перемножаемых векторов; 3)     векторы , ,  образуют правую тройку. Из условия (1) следует, что модуль вектора численно равен площади параллелограмма, построенного на векторах  и  как на сторонах (рис 17): , .

Свойства векторного произведения:

1)     ;

2)     ;

3)     ;

4)     , или , или ;

4a) .

17.Смешанное произведение и его свойства.Условие компланарности векторов.

Смешанным, или векторно-скалярным произведением трех векторов (обозначается ) называется произведение вида .

 Свойства:

• Коммутативность

• ассоциативность

Теорема. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю

Доказательство. Необходимость. Пусть векторы , ,  компланарны. Можно считать, что они лежат в одной плоскости. Тогда вектор  перпендикулярен этой плоскости, следовательно, ,

а значит, их скалярное произведение равно нулю, то есть .

Достаточность. Пусть . Предположим, что векторы некомпланарны. Но тогда существует параллелепипед, построенный на этих векторах, объем которого , а это противоречит условию . Следовательно, предположение неверно, и векторы компланарны.