Замечание

Прямо из определения следует, что график касательной прямой проходит через точку (x₀,f(x₀)). Угол α между касательной к кривой и осью Ох удовлетворяет уравнению

где обозначает тангенс, а  — коэффициент наклона касательной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Вычисление производной функции y=sin x.

Найти производную функции  y(x) = sin x.

Решение.

Используя определение производной, получаем

     

Применим тригонометрическое тождество

     

Тогда

     

Первый предел в данном выражении равен

     

Поскольку , то для производной синуса получаем окончательное выражение:

     

50. Вычисление производных функций: y=C,y=LOG a X, y=ln x.Вычисление производной функции y=cos x.

Воспользуемся математическим определением производной функции:

1.            

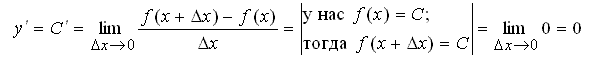
Остальные по образцу

2. Пусть ( ). Тогда приращение функции равно (h=∆x)

а разностное отношение --

Теперь вычислим производную:

При вычислении предела мы, во-первых, воспользовались непрерывностью логарифмической функции и переставили знаки предела и логарифма; во-вторых, сделали замену , при этом при ; в-третьих, был использован второй замечательный предел: . Из полученной формулы

при вытекает, что

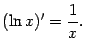
3.

Пусть . Тогда приращение функции равно

а производная --

При этом мы воспользовались непрерывностью синуса, откуда и первым замечательным пределом.

51. Производные суммы, разности, производения, частного двух функций. Вычисление производной функции y=tg x.

Правила дифференцирования.

Пусть u = u(x) и v = v(x) – функции, дифференцируемые в точке х. Тогда в этой точке дифференцируемы функции u+v, uv, . Последнее при условии, что v(x)  0. Причем

(u+v)' = u'+v'

(uv)' = u'v+uv'

Следствием последних трех соотношений являются следующие два: (сu)' = cu', где с – константа, и (u-v)' = u'-v'

Используя правило нахождения производной частного, легко получаются формулы:  и , которые выполняются для любого х, при котором существует tgx и cosx  0 или существует ctgx и sinx0.

52.Производная сложной функции.Вычисление производной показательной функции y= a^x

Пусть y = f(u) и u = (x). Тогда функция y = f((x)) называется сложной функ­цией от х.

Теорема . Если функция u=(x) имеет производную u'_x в точке х, а функ­ция y = f(u) имеет производную у'_u в соответствующей точке u, то сложная функция y = f((x)) в точке х имеет производную у'_x, причем у'_x = у'_u u'_x.

Доказательство. Дадим х приращение Δх. Тогда u и у получат соответст­венно приращения Δu и Δу. Будем считать, что Δu при Δх0 не принимает зна­чений, равных нулю. Тогда . Так как функция u = (x) дифференцируема, а следовательно, непрерывна, то Δu0 при Δх0. Поэтому . Тогда .

Это означает, что у'_x = у'_u u'_x.

Заметим, что теорема верна и в случае, когда при Δх0

Δu принимает значения, равные нулю.

Найдем сначала производную функции у=е^х. Придав аргументу х приращение ∆х, находим приращение функции ∆у: ∆у=е^х+∆х-е^х =е^х(е^∆х-1). Стало быть,

При вычислении предела воспользовались эквивалентностью е^х-l~x при х→0.

Итак, у'=е^х, т.е.

(e^x)'=e^x

Теперь рассмотрим функцию у=а^х, х є R. Так как а^х=e^xlna, то по формуле производной сложной функции находим:

(а^x)'=(е^хlnа)'=e^xlna•(х•lna)'=е^хlnа•lna=a^x•lnа.

Таким образом, (a^х)'=a^хInа.

53.Производная обратной функции.Вычисление производной функции y=arcsin x.

Производная обратной функции

Теорема. Пусть функция х = f(y) монотонна и дифференцируема в некото­ром интервале (a, b) и имеет в точке у этого интервала производную f'(y), не равную нулю. Тогда в соответствующей точке х обратная функция у = f^--1(x) имеет производную [f^--1(x)]', причем

 или

Доказательство. По условию теоремы функция x = f(y) монотонна и дифференци­руема, следовательно, по теореме о существовании обратной функции функция у = f^--1(x) существует, монотонна и непрерывна на соответствующем интервале. Дадим аргументу х приращение Δх0. Тогда функция у = f^--1(x) получит приращение Δу, которое в силу ее монотонности отлично от нуля. Так как функция у = f^--1(x) непрерывна, то Δу0 при Δх0. Тогда .

Пользуясь доказанной теоремой, вычислим производные обратных триго­нометрических функций. Для функции у = arcsinx обратной является функция x = siny, которая является в интервале  монотонной и дифференцируе­мой. Ее производная x' = cosy в этом интервале в нуль не обращается. Поэтому . Таким образом .

Аналогично получаются формулы