6. Понятие определителя.
Вводится только для квадратной матрицы.
Составим произведение из nэлементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца а1 α1 ∙ а2 α2 ∙…∙ аn αn Для удобства первые индексы (номера строк) следуют в порядке возрастания. Вторые индексы (номера столбцов) будут образовывать некоторую перестановку (α1, α2, …, αn). Число различных произведений такого вида будет равно числу различных перестановок из вторых индексов, которое, как мы знаем, равно n!. Домножим каждое из произведений на (-1)k(α1, α2, …, αn). Этот множитель может принимать значения -1…1. Получаем: (-1)k(α1, α2, …, αn)∙ а1 α1 ∙ а2 α2 ∙…∙ аn αn
Сумма всех различных произведений такого вида называется определителем матрицы А. Обозначается |A| = детерминант.
Здесь суммирование производится по всем различным перестановкам вторых индексов det(aij). Очевидно, что число слагаемых в правой части равно n!.
7. Частные случаи определителей.
1) матрица первого порядка:
А1=[a11]
detA1=(-1)k(1)=10 ∙a11=a11
K(1) = 0
2) матрица второго порядка:
detA2
=
3) матрица третьего порядка:
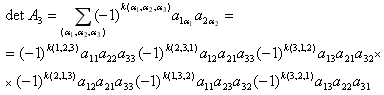
Теорема1: определитель произведения двух квадратных матриц одинакового порядка = произведению их определителей.
det(А1∙А2)= detA1∙detA2
Теорема 2: если аα1β1а α2β2… аαnβnесть произведение элементов матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, то det матрицы может быть найден по формуле:
detA=∑(-1) к(α1, α2... αn) к(β1, β2...βn)∙аα1β1а α2β2… аαnβn.
Здесь суммирование берётся по всевозможным произведениям элементов, взятых по 1му и только по 1му из каждой строки и каждого столбца матрицы А. эту теорему можно рассматривать как другое определение определителя равносильное тому, которое было введено ранее.
10. Теоремы о разложениях определителя
Теорема 1 (о разложении определителя по эл-там ряда). Определитель = сумме произведений элементов любого его ряда на их алгебраические дополнения,
Для строк эта теорема выглядит так:
detА= аi1Аi1+аi2Аi2+…+..ainAin
Для столбцов:
detА=a1jA1j+ a2jA2j+…+ anjAnj.
Теорема 2 (замещения). Сумма произведений чисел α1, α2... αn на алгебраические дополнения элементов некоторого ряда определителя = определителю, полученному из данного заменой в нём элементов выбранного ряда на числа α1, α2... αn.
Теорема 3 (аннулирования). Сумма произведений элементов некоторого ряда определителя на алгебраические дополнения элементов другого, параллельного ему ряда, = 0.
Справедливость этой теоремы вытекает из того, что такая сумма произведений, согласно теореме замещения, будет = определителю, имеющему 2 одинаковых параллельных ряда, который согласно одному из св-в определителя = 0.
8. Свойства определителей.
1. При транспонировании матрицы её определитель не изменяется. det AT=det A. Это свойство следует из другого определения определителя.
Рядом определителя будем называть его строку или столбец.
2. Если все элементы некоторого ряда определителя = 0, то этот определитель = 0.
Это свойство следует из определения определителя, согласно которому каждое слагаемое в определителе должно содержать 1 элемент из каждого ряда, в т. ч. из нулевого, => все слагаемые определителя = 0. Это и означает равенство нулю определителя.
3. Если все элементы некоторого ряда определителя имеют общий множитель, то этот множитель можно вынести за знак определителя.
Следует из определения определителя. Согласно определению, в каждом слагаемом определителя будет присутствовать 1 элемент из рассматриваемого ряда, т. е. каждое слагаемое определителя будет содержать этот множитель. Вынося этот множитель за скобки (или за знак суммы) в скобках получим определитель без общего множителя.
4. Определитель, каждый элемент некоторого ряда которого равен сумме 2-х слагаемых, равен сумме 2-х определителей, в первом из которых в данном ряду стоят первые слагаемые, а во втором – вторые слагаемые. А элементы остальных рядов у всех 3х определителей совпадают.
Это св-во для столбцов можно записать так:
Действительно, согласно определению определителя, каждое слагаемое будет содержать эл-ты из данного ряда, яв-ся суммой 2-ух слагаемых. Поэтому каждое слагаемое в определителе в левой части формулы разобьется на 2 слагаемых. Число слагаемых в определителе удваивается. Группируя отдельные слагаемые, содержащие а'ni и a''ni, получим две суммы, которые, согласно определению, дадут первый и второй определитель из правой части.
5. Если м-ца В, полученная из м-цы А переменой мест 2х её параллельных рядов, то detВ=-detА, т. е. при перемене мест строк и столбцов матрицы знак её определителя изменится на противоположный. Действительно, например, перемена мест столбцов приведет к транспозиции – перестановке вторых индексов. В рез-те четность этой перестановки изменится. Поэтому, согласно определению определителя, изменятся знаки всех слагаемых определителя, а => поменяется на противоп. знак определителя.
6. Если м-ца имеет 2 одинаковых параллельных ряда, то её определитель = 0. Действительно, поменяв местами 2 одинаковых ряда м-цы, мы получим ту же самую матрицу. Но, согласно предыдущему свойству, ее определитель должен изменить знак на противоположный. detA=-detA. Это возможно только если detA=0.
7. Определитель м-цы, имеющий 2 пропорциональных параллельных ряда=0. Действительно, вынося коэффициент пропорциональности рядов за знак определителя, получим определитель, имеющий 2 одинаковых параллельных ряда, который, согласно св-ву 6, = 0.
8. Если м-ца В, полученная из м-цы А прибавлением к эл-там некоторого её ряда эл-тов другого параллельного ему ряда, умноженных на некоторое число, то detВ= detА.