49. Сравнение бесконечно малых

Пусть одновременно несколько ф-ций α, β, γ… от одного аргумента х явл. ∞ малыми, т.е. →0 при х→а либо при х→∞, далее мы не будем указывать к чему →х, предполагая один из этих случаев. limα=0, limβ=0, limγ=0.

Определение. Если отношение имеет конечный предел, отличный от 0, , то ∞ малые α и β наз. ∞ малыми одинакового порядка. В этом случае

Определение. Если отношение 2-х ∞ малых →0 (тогда очевидно ), то ∞ малая β наз. ∞ малой высшего порядка относительно ∞ малой α.

Определение. Если сущ. конечный предел (а тогда очевидно, существует и предел ), то ∞ малая β наз. ∞ малой порядка k относительно ∞ малой α.

Определение. Если (а тогда очевидно, ), то α и β - эквивалентные ∞ малые.

Пример: 2х и sin3х явл. ∞ малыми, при х→0. Действительно,

Найдем пределы отношений

Отсюда следует: эти ∞ малые одинаково порядка.

Т-ма: Если α и β эквивалентные ∞ малые, то их разность явл. ∞ малой высшего порядка относительно α или β.

Док-во: Т.к. α и β эквивалентны, то (по определению). Найдём предел

Таким образом, α-β – ∞ малое высшего порядка относительно α.

Аналогично можно доказать, что

Справедлива также обратная т-ма: если разность α-β - ∞ малая высшего порядка, чем α, чем β, то α и β – эквивалентные бесконечно малые.

Док-во: если , отсюда следует α~β.

Замечаем: Если отношение 2-х ∞ малых не имеет предела и этот предел ≠∞, то эти ∞ малые несравнимы в смысле данных выше определений.

Т-ма: Предел отношения 2-х ∞ малых не изменится, если числитель и знаменатель заменить эквивалентными ∞ малыми.

50.Производная.

Пусть некот. тело движется неравномерно. Пусть закон по кот. измен-ся пройденный путь, в зависимости от времени, опред-ся ф-цией s=s(t). Для опред-ия быстроты движения выводят понятие средней

Мгновенную скорость можно определить как предел

Мгновенная v есть производная от пути по времени.

Пусть дана ф-ция y=f(x). Дадим переменной х приращение Δх. Тогда ф-ция у получит приращение Δу=f(x+Δx)-f(x). Если сущ. предел отношения приращения ф-ции к приращению аргумента, когда приращение аргумента →0, то этот предел называется производной от ф-ции f(x) и обознач. f ’(x). Таким образом, по определению: или

С учетом данного опред. мгновенная v есть v(t)=s’(t)

Обозначения производной: f’(x); у’(x);

В конкретной точке f’(x₀); у’(x₀).

Физический смысл производной – это v изменения ф-ции в зависимости от изменения аргумента. Операция по нахождению производной - дифференцирование.

Найдем производную ф-ции y=cos x по опред-ию производной: дадим ф-ции х приращениеΔх, тогда ф-ция y получит приращение: Δу=cos(x+Δx)-cos x.

Разность косинусов равна

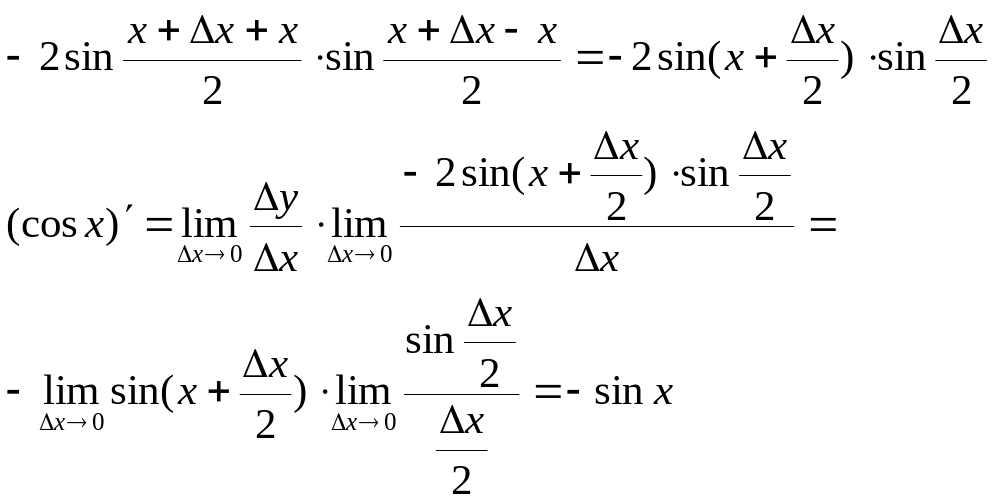
(cosx)’=-sin х

Аналогично можно доказать, что (sin х)’=cos x

С помощью определения производной найдем производную ф-ции у=х². Если х изменяется на Δх, у изменяется на Δу= (х+Δх)²-х²=х²+2хΔх+Δх²-х²=2хΔх+Δх²

(х²)’=2х. Эта формула является частным случаем более общей (xⁿ)’=nx^n-1

51. Геометрический смысл производной

Пусть дана некоторая кривая на плоскости. Выделим на ней некоторые т. М₀ и М₁, проведём через них секущую, затем т. М₁ будет приближаться к т. М₀.

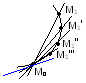
Определение. Если при неограниченном приближении точки М₁ по кривой к точке М₀ с любой стороны секущая М₀М₁ стремится занять положение некоторой прямой, то эта прямая называется касательной к данной кривой в точке М₀.

Рассмотрим график ф-ии y=f(x)

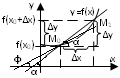
Из ∆ видно, что - tg угла наклона секущей по отношению к положительному направлению оси Ох.

Перейдём к пределу при ∆х→0

При уменьшении ∆х, точка _М1 будет приближаться к точке _М0.

В пределе секущая _М0_М1 перейдёт в касательную к графику в точке _М0. В результате

Производная функции y=f(x) в точке x₀ = tg угла наклона касательной к графику этой ф-ии в т. (x₀,f(x₀)) по отношению к положит. направлению оси Ох.