37. Поверхности второго порядка.

1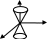 ) z

y

x

2) трехосный эллипсоид

a, b, с – полуоси

a=с

a=b=c= R

- уравнение сферы

3)

Однополостный гиперболоид

4)

Двухполостный гиперболоид.

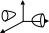
5)

pq>0 – элииптический параболоид

6)

г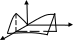 иперболический параболоид

7) - эллиптический цилиндр

8) - гиперболический цилиндр

9) =2px – параболический цилиндр

39. Предел переменной величины.

Постоянное число a наз. пределом переменной величины x, если для любого сколько угодно малого числа Е> 0 можно указать значение переменной величины x такое, что для всех её послед. значений будет выполняться неравенство │х-а│<E, а – такое число, что все последующие переменные будут лежать в этом интервале. limx=a. Частным случаем понятия предела переменной величины явл. понятие предела числовой последовательности. Число а наз. пределом числовой последовательности x₁,x₂,…,x_n, если для любого сколько угодно малого числа Е>0 можно указать такой номер N, что для всех n>N, справедливо неравенство: |Хn-a|<E.

Постоянное число а есть предел переменной х, если для любой сколько угодно малой E окрестности числа а можно указать значение переменной х такое, что все последующие ее значения будут лежать внутри этой окрестности.

40. Ф-ция и её предел.

Если каждому значению одной переменной величины х ставят в соответствие единственное значение другой переменной величины у, то переменную у наз-ют зависимой переменной или функцией от х, а переменную х при этом наз-ют независимой переменной, или аргументом. y=f(x), y=φ(x), y=y(x). Функция y=f(x) наз-ся монотонно возрастающей (монотонно убывающей), если большему значению её аргумента соответствует большее (меньшее) значение функции. Постоянное число b наз-ся пределом функции y=f(x) при x стремящемся к а, если для любого сколько угодно малого числа ε>0 можно указать число δ>0, что для всех значений х, удовлетворяющих неравенству ׀x-a׀<δ(∆) будет выполняться условие ׀f(x)-b׀<ε.

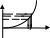Lim_х→аf(x)=b

y

b+ε

b

b-ε

a- δ a a+ δ

Геометрически это означает следующее: число b наз-ся пределом функции y=f(x) x→a, если для любой сколько угодно малой Е окрестности числа b можно указать ∆ окрестность числа а такую, что если значение аргумента х € этой δ-окрестности, то значение функции y=f(x) будет принадлежать заданной E окрестности. Заметим, что переменная величина х не может иметь двух пределов.

41. Бесконечно малые и бесконечно большие.Теоремы.

Переменная величина х стремиться к ∞, если для любого сколько угодно большого числа M>0 можно указать такое значение этой переменной величины, что для всех последующих значений переменной величины будет выполняться неравенство |х|>М. Обозначают limx=∞. Если переменная величина х стремится к бесконечности, принимает только + значения (только -), то пишут limx=+∞ (limx=-∞).

Если переменная величина →∞, то она называется бесконечно большой.

Е сли функция y=f(x) стремится к пределу b, при х→а так, что х при этом принимает только значения меньшие, чем а, то число b₁ наз-ся пределом функции f(x) при x→a слева обознач. . Если f(x) стремится к пределу b₂ (x→a-0), что х при этом принимает значение только больше, чем а, то число b₂ наз-ся пределом ф-ции f(x) справа точки а и обозначается .

Можно показать, что если для ф-ции f(x) в точке а оба предела слева и справа существуют и равны друг другу , то предел слева и справа – односторонние пределы. В этом случае существует предел ф-ции f(x) при х→a= b в смысле, определённо ранее.

Функция f(x) стремится к бесконечности, т.е. яв-ся бесконечно большой при х→а, если для любого сколько угодно большого числа М>0 можно указать число ∆ такое, что для всех знач. х удовлетворяющих неравенству |x-a|<δ будет выполняться условие ׀f(x)׀>M.

Если при этом f(x) принимает только положительные значения, то пишут , если только отриц., то

Функция f(х) называется бесконечно малой при х→а либо при х→∞, если

Теорема. Если функция у=f(х) может быть представлена в виде суммы бесконечно малой функции α(х) и числа b, то limf(x)=b. Справедливо также обратное утверждение: если limf(x)=b, то функция f(x) может быть представлена в виде f(x)=α(x)+b, где α(х) - бесконечно малая функция. Это утверждение справедливо как при х→а, так и при х→∞.

Доказательство для случая х→а.

Пусть f(x)=α(x)+b, где (1), тогда, по определению предела, для любого сколь угодно малого Е>0 можно указать число δ>0 такое, что для всех значений х, удовлетворяющих неравенству |x-a|<δ будет выполняться неравенство |α(x)-0|<E или |α(x)|<E. Но, согласно равенству (1), α(x)=f(x)-b, тогда из предыдущего нерав-ва имеем: |f(x)-b|<E, а это означает, что . Аналогично доказывается 2 часть теоремы.

Теорема. Если функция α(х) →0 при х→а, т.е. яв-ся бесконечно малой, но не обращается в 0 при х=а, то функция f(x)=1/ α(х)→∞ при х→а, т.е яв-ся бесконечно большой.

Теорема. Алгебраическая сумма любого конечного числа бесконечно малых есть бесконечно малое.

Произведение любого конечного числа бесконечно малых является бесконечно малым.

Теорема. Произведение бесконечно малой функции α(х) на ограниченную f(х) есть функция бесконечно малая.

Следствие: произведение бесконечно малой на постоянную есть бесконечно малое.

Теорема. Частное α(х)/f(х) от деления бесконечно малой на функцию f(х) предел которой отличен от 0 есть бесконечно малое.