52. Основные правила дифференцирования.

Если производная ф-ции y=f(x) в точке x₀ существует, т. е. существует предел , то f(x) называется дифференцируемой в точке х₀.

Если ф-ция дифференцируема в каждой точке некоторого интервала (a,b) или некоторого отрезка [a,b], то она называется дифференцируемой на данном интервале или на данном отрезке.

Теорема 1. Если ф-ция y=f(x) дифференцируема в некоторой точке х₀, то она непрерывна в этой точке.

Док-во. Дифференцируемость ф-ции f(x) в точке х₀ означает существование предела . Как мы знаем, каждая ф-ция отличается от своего предела на бесконечно малое слагаемое, т. е. .

Умножаем обе части на ∆х. Имеем:

Перейдём в последнем равенстве к пределу при ∆х→0. Имеем

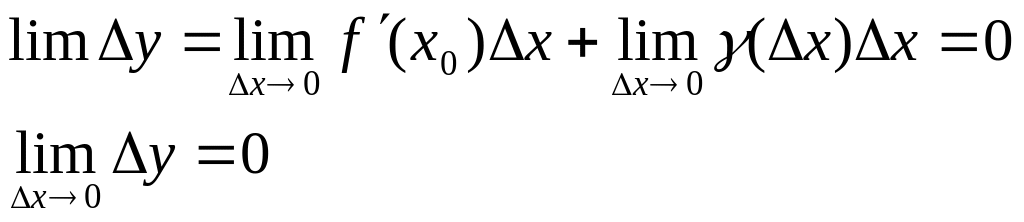
Это и означает непрерывность функции в точке х₀.

Теорема 2. Производная от постоянной = 0. с’=0, если с=const.

Док-во. Если у=с=const, то Δу=f(x+Δx)-f(x)=с-с=0. Приращение ф-ции всегда = 0.

Теорема 3. Постоянный множитель можно выносить за знак производной.

(сf(x))’=cf’(x)

Док-во.

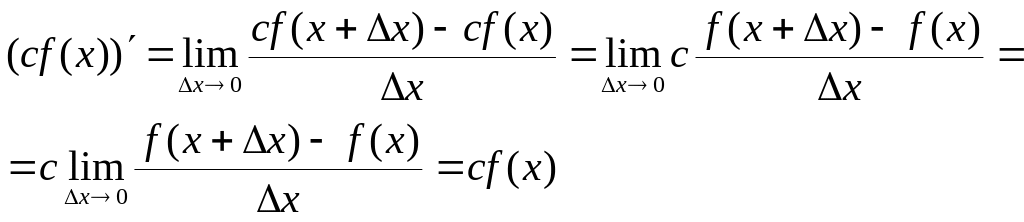
Теорема 4. Производная от суммы ф-ций = сумме их производных. Т. е. (U(x)+V(x))’=U’(x)+V’(x)

Док-во.

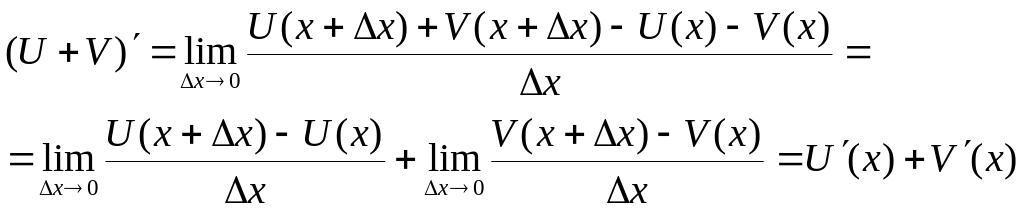
Теорема 5. Производная от произведения 2х дифференцируемых ф-ций может быть найдена по формуле (U∙V)’=U’∙V+U∙V’

Док-во. Пусть даны 2 дифференцируемые непрерывные ф-ции U(x), V(x). y= U∙V.

Дадим переменной приращение ∆х, тогда ф-ции U, V, y получат соответственно приращения ∆U, ∆V, ∆y. Очевидно, что у+∆у=(U+∆U)∙(V+∆V), тогда ∆у=(U+∆U)∙(V+∆V)-у. Тогда ∆у=UV+U∆V+V∆U+∆V∆U-UV. Разделим обе части равенства на ∆х. Тогда , перейдем к пределу при Δх→0. Имеем

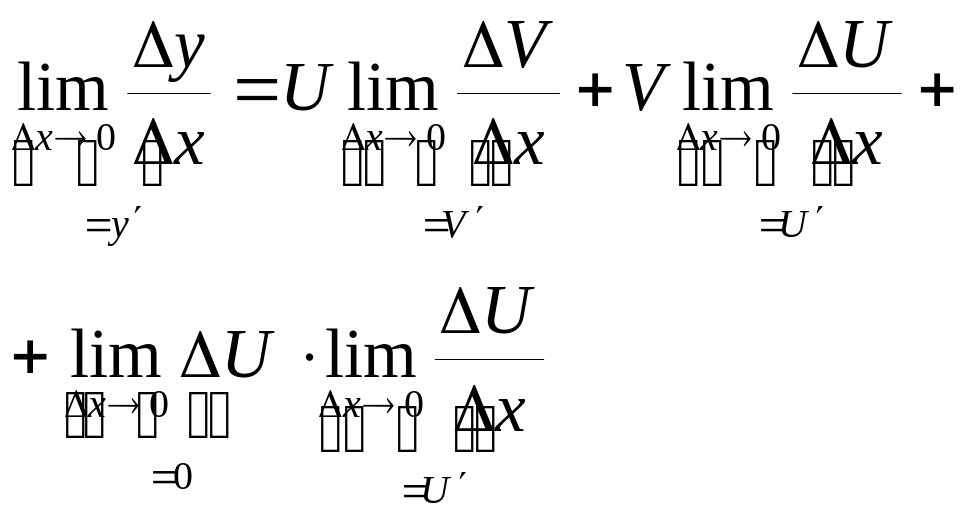
Получили y’= U∙V’+U’∙V

(U∙V)’=U’∙V+U∙V’. теорема доказана.

Эту теорему можно обобщить на произвольное число сомножителей. (U₁∙U₂∙…∙U_n)= U₁’∙U₂∙…∙U_n+ U₁∙U₂’∙…∙U_n+…+ U₁∙U₂∙…∙U_n’

Теорема 6.Производная от частного 2х дифференцируемых ф-ций может быть найдена по формуле

54. Обратная функция и её дифференцирование.

Пусть дана монотонная функция y=f(x) (монотонно возрастающая или монотонно убывающая). Для определённости рассмотрим монотонно возрастающую функцию.

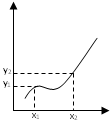
Тогда различным значениям аргумента х₁ и х₂ соответствуют различные значения функции: y₁=f(х₁) и у₂= f(х₂). Причём, это справедливо только для монотонной функции. Т.е. для монотонной функции существует взаимно однозначное соответствие между значениями х и y.

Каждому значению y соответствует единственное значение х и в данном случае формально можно считать, то переменная х является функцией от y.

X=_φ(y).

Эта функция X=_φ(y) называется обратной по отношению к функции y=f(x) .

Теорема: Если для функции y=f(x) существует обратная функция X=_φ(y), имеющая в некоторой точке у производную _φ’(y), то ф-ция y=f(x) имеет производную в соответствующей точке X=_φ(y), кот. может быть найдена по формуле

Доказательство: Дадим приращение ∆у, тогда переменная х получит приращение ∆х=φ(х+∆х)-φ(х).

В силу монотонности f(x) и φ(х), ∆у≠0 и ∆х≠0.

Т.к. в этом случае

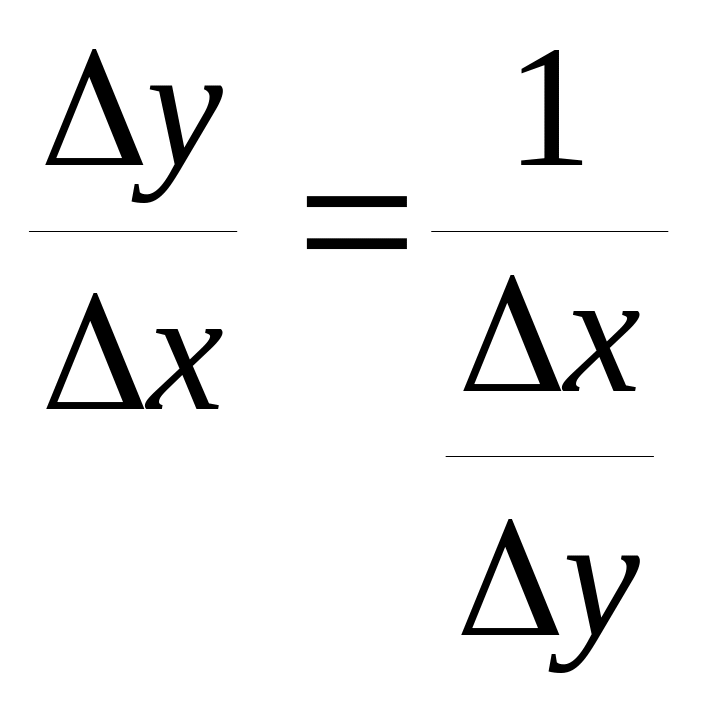
Перейдём в обеих частях этого равенства к пределу при ∆х→0, тогда и ∆у→0.

Имеем: 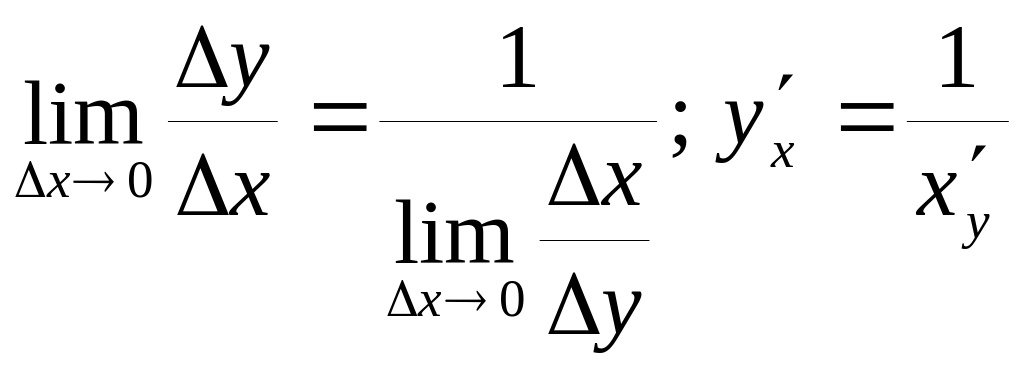. ч.т.д.