5. Дифференциал функции

Пусть функция y=f(x) дифференцируема в точке x, тогда ее приращение можно записать в виде двух слагаемых, первое из которых линейно относительно x, а второе бесконечно малое при Dx0 более высокого порядка малости по сравнению с Dx:

, где (Dx)  0 при Dx  0.

Определение 4. Слагаемое f’(x) Dx называется главной линейной относительно Dx частью приращения функции y = f(x), называемой дифференциалом этой функции. Дифференциал обозначается

dy = y' (x) Dx .

Если x – независимая переменная, то справедливо равенство: Dx = dx, так как (x)' = 1. Тогда формула для дифференциала записывается:

dy = y' (x) dx .

Так как второе слагаемое приращения функция – малая величина более высокого порядка малости по сравнению с Dx, то между приращением функции и ее дифференциалом можно поставить приближенное равенство. Это равенство тем точнее, чем меньше Dx. На основе этого приближенного равенства получается приближенное представление значения дифференцируемой функции:

Пример. Вычислить приближенно

Решение. Рассмотрим функцию . В качестве начальной точки возьмем x₀ = 4, приращение Dx = 0,08, .

Подставим в формулу:

, где D<<0,08.

Геометрический смысл дифференциала

Рассмотрим график дифференцируемой функции в некоторой окрестности точки x₀ (рис.6):

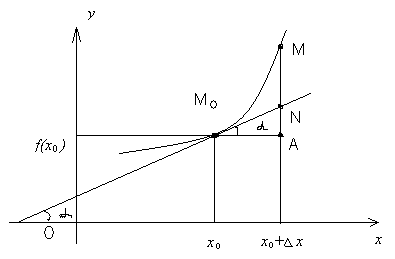
Рис. 6

из DM₀AN: AN = M₀Atg = Dxf '(x₀) = dy

Итак: дифференциал функции y = f(x) в точке x₀ равен приращению ординаты касательной (AN), проведенной к кривой y = f(x) в точке (x₀; f(x₀)), при переходе от x₀ к x₀+x (от точки М₀ в точку М).

Инвариантность формы дифференциала

Теорема 14. Пусть функция y=f(U) дифференцируема в точке u, а функция u = u(x) дифференцируема в соответствующей точке x(u=u(x)). Тогда для сложной функции y = f(u(x)) справедливо равенство:

dy = f ' (u)du = y' (x)dx

Доказательство. Сложная функция y=f(u(x)) является дифференцируемой функцией в точке x. Поэтому справедливо равенство:

dy = y' (x)dx

Но так как функция y(x)=f(u(x)) сложная функция, то

y' (x) = f’(u)  u' (x)

Поэтому dy = y' (x)dx = f’(u)u' (x)dx = f’(u)du, так как по условию теоремы функция U = U(x) дифференцируема в точке x

du = u' (x)dx.

Теорема доказана.

6. Производные и дифференциалы высших порядков

Если функция y = f(x) дифференцируема на некотором промежутке, то она имеет на этом промежутке производную y' = f’(x), которая в свою очередь, может иметь производную: (y')' = (f’(x))' = y'', называемая второй производной для функции y = f(x). Она обозначается:

Может случиться, что новая функция y''(x) имеет производную, она называется третьей производной для функции y=f(x). Ее обозначения:

Производная “n”-ого порядка функции y=f(x) обозначается:

Вторым дифференциалом функции y = f(x) в точке x называется выражение, обозначаемое d²y и вычисляемое по формуле:

,

если x – независимая переменная.

Дифференциал третьего порядка функции y = f(x):

,

если x – независимая переменная. И так далее.

Замечание: дифференциал уже второго порядка не обладает свойством инвариантности формы.