3. Экстремумы функции
Определение 6. Функция y=f(x) x0Î D(f) максимум ymax (минимум ymin), если существует такая, окрестность точки x0, для всех x из которой выполняется неравенство:
f(x0) > f(x) (f(x0) < f(x)).
Определение 7. Точки максимума и минимума функции называются точками экстремума функции.
Теорема 3 (необходимое условие экстремума)
Если функция y = f(x) имеет экстремум в точке x0, то в этой точке производная функции равна нулю или не существует.
Доказательство.
1) Для определенности рассмотрим случаи, когда функция y = f(x) в точке x0 имеет максимум и в этой точке существует производная. Тогда из определения максимума для любого x, принадлежащего окрестности точки x0 f(x0) > f(x).
Отсюда следует, что для любого x 0 справедливо неравенство: f(x0+x) - f(x0) < 0. Разделим неравенство на Dx. При этом получим:
при Dx
> 0:
при Dx
< 0:
Перейдем к пределам:
Так как f”(x0) существует, то:
f’(x0+0) = f’(x0-0) = f(x0) = 0.
Аналогично рассматривается случай, когда x0 – точка минимума.
2) Если f' (x0) не существует или равна ¥, то точка x0 может быть точкой экстремума функции.
Например, функция y = 1х1 имеет минимум при x = 0, хотя y' (0) не существует (рис.9)
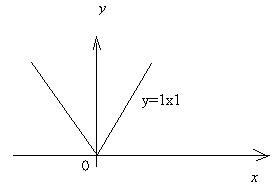
Рис. 9
Теорема доказана.
Теорема 4 (достаточное условие экстремума)
Если функция y = f(x) непрерывна в точке x0, дифференцируема в некоторой ее окрестности за исключением, может быть, самой этой точки, f’(x0) = 0 или не существует и при переходе x через точку x0 f’(x) изменяет знак, то точка x0 является точкой экстремума. Если при этом знак f’(x) меняется.
с «+» на «-», то x0 - точка максимума,
с «-» на «+», то x0 - точка минимума.
Доказательство. Пусть f’(x) при переходе x через точку x0 изменяет знак с «+» на «-», то есть f’(x)>0 при x Î (x0-; x0)
и f’(x)<0 при x Î (x0;x0 +), где >0.
(рис.10).
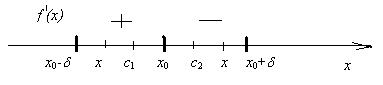
Рис. 10
1) Пусть x Î (x0-; x0). На отрезке [x;x0] функция y = f(x) удовлетворяет теореме Лагранжа (по условию теоремы 4). Значит, на (x;x0) найдется хотя бы одна точка c1, в которой выполняется равенство:
f(x) – f(x0) = f’(c1)(x–x0), где c1(x0-;x0).
Так как f’(c1) > 0 и x-x0 < 0, то f(x) – f(x0) < 0
2) Пусть x Î (x0;x0 +). На отрезке [x;x0] функция y = f(x) также удовлетворяет теореме Лагранжа. Значит на (x0;x) найдется хотя бы одна точка с2, в которой выполняется равенство:
f(x) – f(x0) = f’(c2)(x–x0), где c2 (x0;x0+).
Так как f’(c2) < 0 и x-x0 > 0, то f(x) – f(x0) < 0
Следовательно, для любого x Î (x0-d;x0 +d) выполняется неравенство:
f(x0) > f(x).
Отсюда следует, что точка x0 является точкой максимума функции y = f(x).
Аналогично рассматривается случай, когда f’(x) при переходе x через точку x0 изменяет знак с «+» на «-». При этом точка x0 является точкой минимума функции.
Теорема доказана.
4. Выпуклость, вогнутость и точки перегиба графика функции
Пусть функция y = f(x) дифференцируема в любой точке промежутка (a;b). Тогда она имеет конечную производную в любой точке этого промежутка. Значит, существует касательная к графику функции y = f(x) в любой его точке (x;f(x)), a < x < b.
Определение 8. График функции y = f(x), дифференцируемой в каждой точке промежутка (a;b) называется выпуклым (вогнутым) на этом промежутке, если для любого x Î (a;b) график расположен не выше (не ниже) касательной к графику в точке (x;f(x)).
Теорема 5 (достаточное условие выпуклости или вогнутости кривой).
Пусть функция y = f(x) дважды дифференцируема на промежутке (a;b) и f”(x) для x Î (a;b) сохраняет свой знак, то кривая y = f(x) выпуклая, если f”(x) 0 при x Î (a;b), и кривая y = f(x) вогнутая, если f”(x) 0 при x Î (a;b).
Доказательство. Для определенности рассмотрим случай, когда f”(x) 0 для x Î (a;b). Обозначим x0 любую точку промежутка (a;b). Построим касательную к кривой y = f(x) в точке (x0; f(x0)): yкасат = f(x0) + f(x0)(x- x0). Покажем, что график функции y = f(x) лежит не ниже этой касательной, то есть выполняется неравенство (рис.11):
f(x) – yкасат. (x) 0 для любого x Î (a;b).
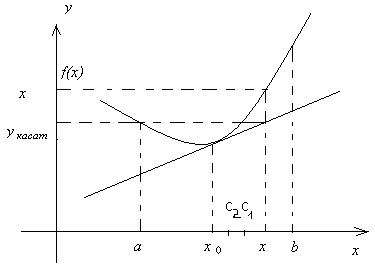
Рис. 11
f(x) – yкасат(x) = f(x) – (f(x0) + f’(x0)(x-x0)) =
=f(x) – f(x0) – f’(x0)(x-x0) = (f(x) - f(x0)) - f’(x0)(x-x0), где x Î (a;b), (1)
На [x0;x] функция y = f(x) удовлетворяет условию теоремы Лагранжа. То есть на [x0;x] найдется хотя бы одна точка c1, для которой выполняется равенство:
F(x) – f(x0) = f’(c1)(x-x0).
Поставим в равенство (1) полученное соотношение:
f(x) – yкасат(x) = f’(c1)(x-x0) – f’(x0)(x-x0) = (x-x0)(f’(c1) – f’(x0)). (2)
На [x0;c1] функция f’(x) удовлетворяет условию теоремы Лагранжа. То есть на (x0;c1) найдется хотя бы одна точка с2, для которой выполняется равенство:
f’(c1) – f’(x0) = f”(c2)(c1-x0).
Подставим в равенство (2) полученное соотношение:
f(x) – yкасат(x) = (x-x0)f”(c2)(c1-x0). (3)
Если x > x0, то c1 > x0 и c2 > x0, то есть x-x0 < 0 и с1-x0 < 0.
По предположению f”(x) 0. Тогда f(x) – yкасат(x) 0.
Если x < x0, то c1 < x0 и c2 < x0, то есть x-x0 > 0 и c1-x0 > 0.
Тогда f(x) – yкасат(x) 0.
Следовательно, при любом x Î (a;b) выполняется неравенство:
f(x) – yкасат(x) 0.
Аналогично можно доказать, что если f”(x) 0 при любом x Î (a;b), то кривая y = f(x) на (a;b) будет выпуклой.
Теорема доказана.
Определение 9. Пусть в точке (x0;f(x0)) существует касательная. Тогда точка (x0;f(x0)), отделяющая выпуклую часть кривой от вогнутой или наоборот называется точкой перегиба графика функции y = f(x).
Теорема 6 (достаточное условие точки перегиба).
Если функция y = f(x) дифференцируема в окрестности точки x0, вторая производная функции f”(x0) = 0 или не существует и f”(x) меняет свой знак при переходе x через точку x0, то точка (x0;f(x0)) – точка перегиба кривой y = f(x).
Доказательство. Для определенности рассмотрим слeчай, когда f”(x) при переходе через точку x0 изменяет знак с «+» на «-».
Тогда в левой полуокрестности точки x0 f”(x) >0, то есть кривая при x < x0 вогнутая, а в правой полуокрестности точки x0 f”(x) <0, то есть кривая при x > x0 выпуклая.
Следовательно, точка (x0;f(x0)) по определению является точкой перегиба графика функции y = f(x).
Аналогично рассматривается другой случай, когда f”(x) при переходе через точку x0 изменяет знак с «-» на «+».
Теорема доказана.