2. Интегрирование рациональных дробей

Задача интегрирования рациональной дроби сводится к умению интегрирования только правильных рациональных дробей, так как интегрирование целой части дроби (многочлена) не сложная. Если решена задача разложения правильной дроби на сумму простых дробей, то дальше надо уметь интегрировать простые дроби. Покажем, как интегрировать такие дроби.

I.

II.

III.

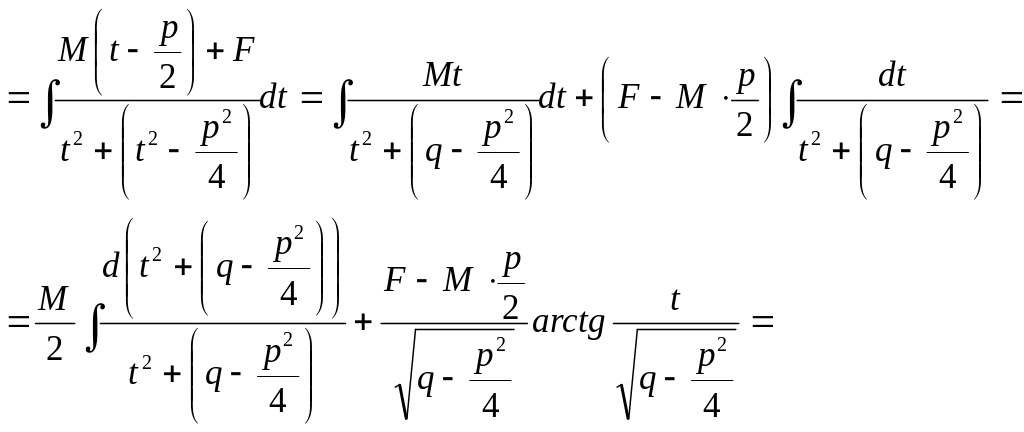
Интегрирование дроби IV типа проводится аналогично интегрированию дроби III типа.

Пример 22.

D = 16 – 52 < 0  дробь III типа.

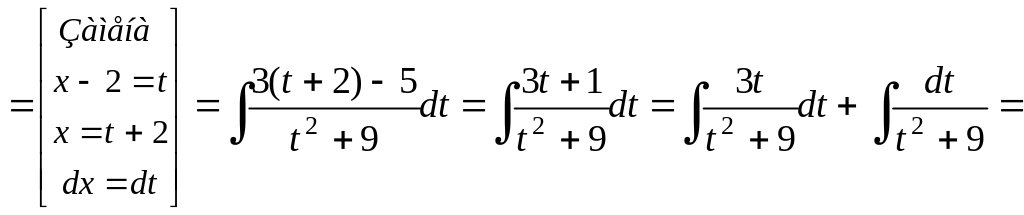
Ответ:

Пример 23.

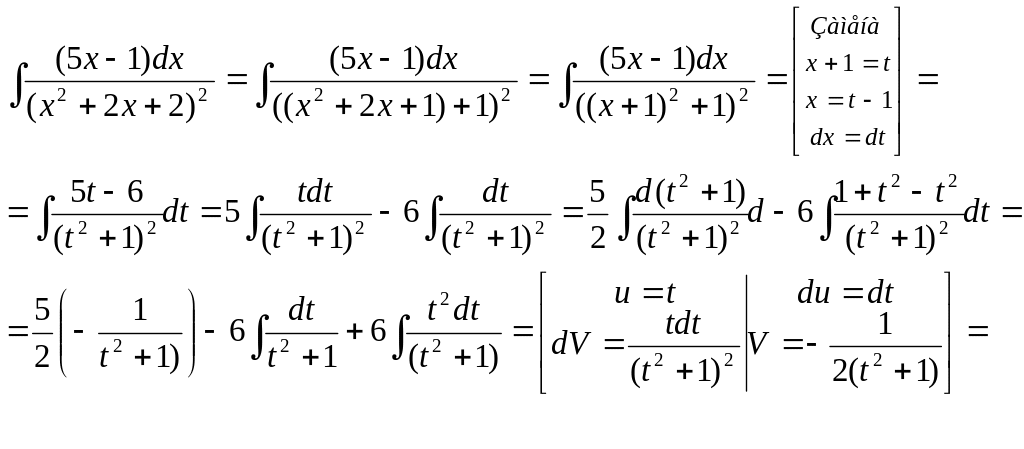
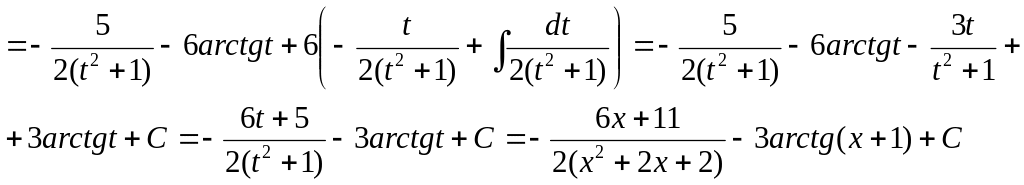
Ответ:

Итак, любая рациональная дробь интегрируема. Для этого необходимо выполнить следующие действия.

1) Если дробь является неправильной, выделить ее целую часть. То есть представить в виде:

,

где T_m-n(x) и R_r(x) – многочлены степени m-n и r соответственно (причем r<n).

2) Разложить правильную рациональную дробь на сумму простых дробей

3) Вычислить интегралы от многочлена T_m-n(x) и каждой из простых дробей, полученных на шаге 2).

Пример 24.

1) Дробь - неправильная рациональная дробь. Выделим ее целую часть:

Поэтому можно записать:

2) Полученную правильную дробь разложим на сумму простых дробей:

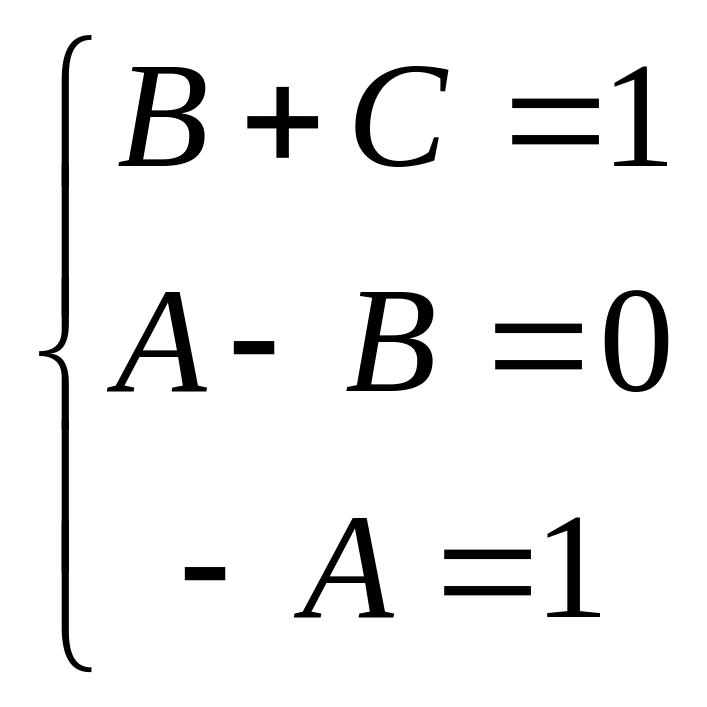
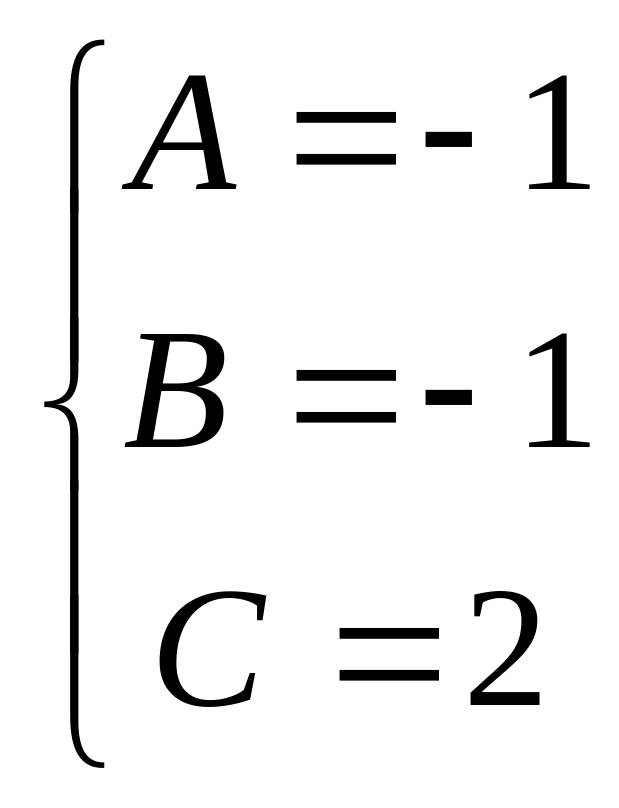
Отсюда следует:

Значит, подынтегральная рациональная дробь представима в виде:

3) Найдем интеграл:

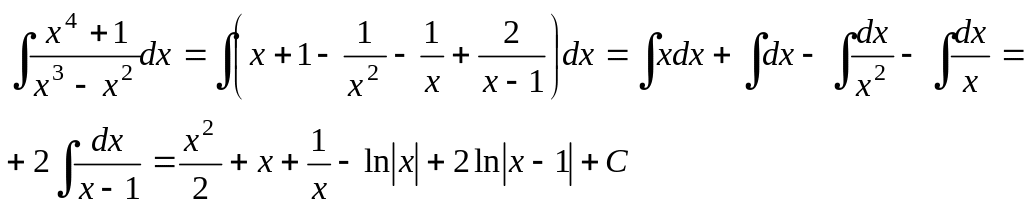
Ответ:

5. Интегрирование тригонометрических выражений

1) Интеграл вида

а) Если n - четное число и m - четное, то подынтегральное выражение преобразуют с помощью формул:

,

б) Если одно из чисел m или n – нечетное, то выполняют замену:

t = sin x, если n – нечетное;

t = cos x, если m – нечетное.

Эта замена приводит к интегрированию степенных интегралов или рациональных дроби.

в) Если оба числа m и n – нечетные, то интеграл берется как в случае замены:

t = sin x, так и t = cos x.

Пример 25.

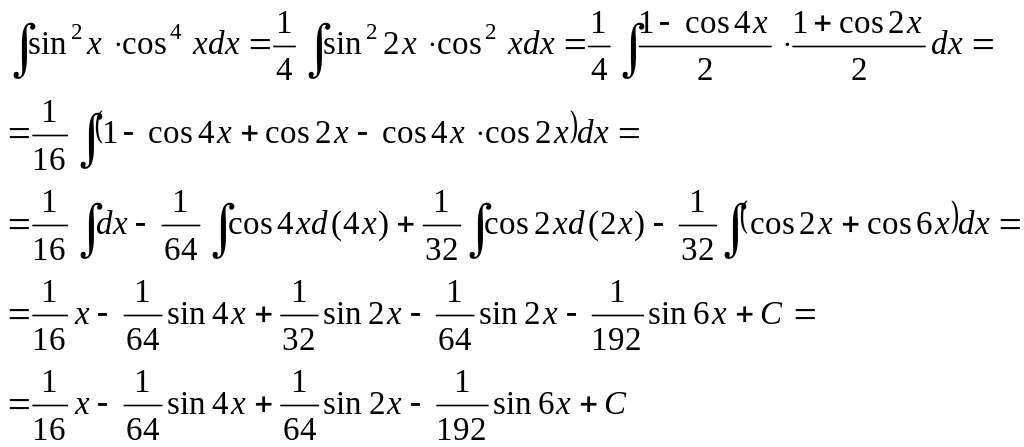
Ответ:

Пример 26.

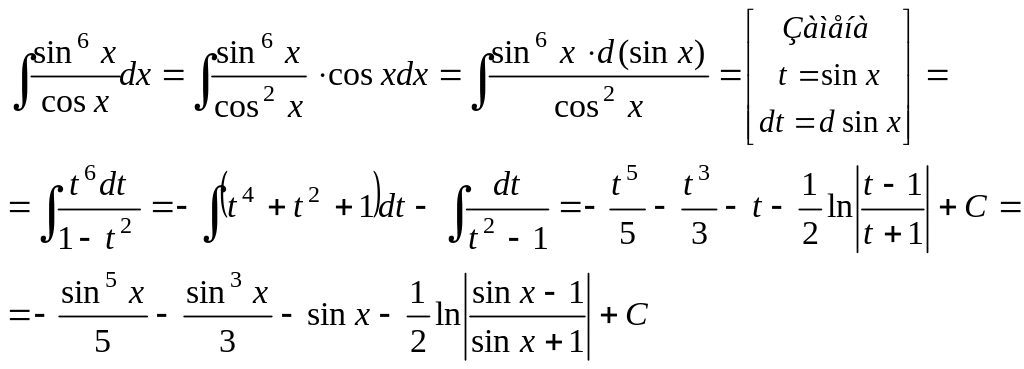
Ответ:

Пример 27.

Ответ:

2) Интегралы вида:

; ; .

Такие интегралы находят после предварительного применения формул:

Пример 28.

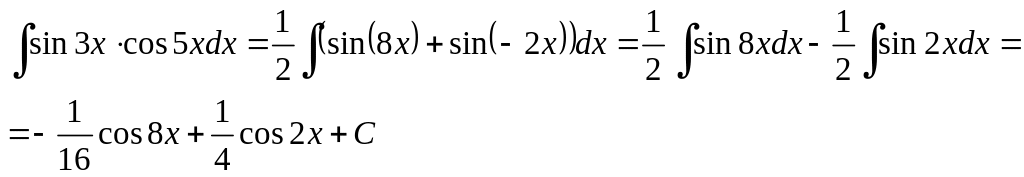
Ответ:

3) Интегралы вида , где f(u;V) – рациональная функция двух переменных.

Такие интегралы приводятся к интегралам от рациональных дробей с помощью замены:

;

;

;

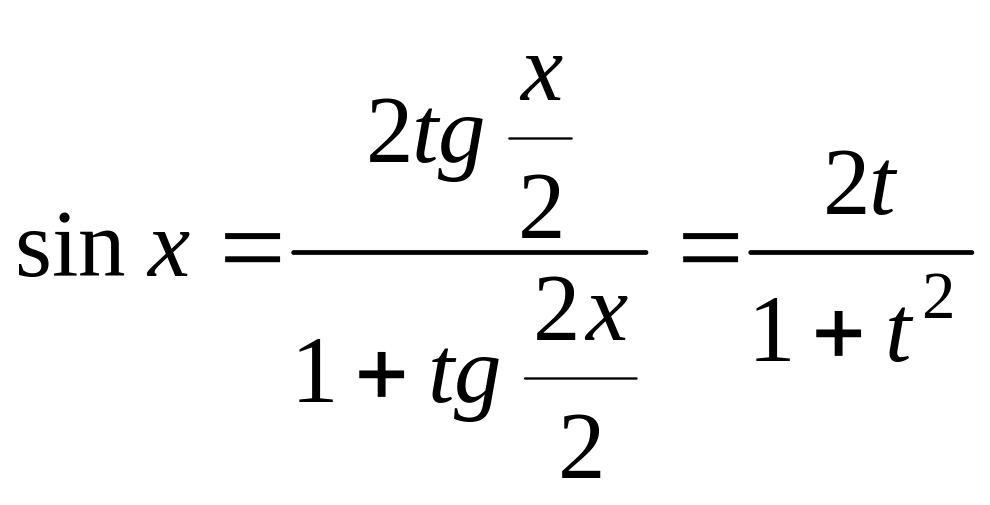Пример 29.

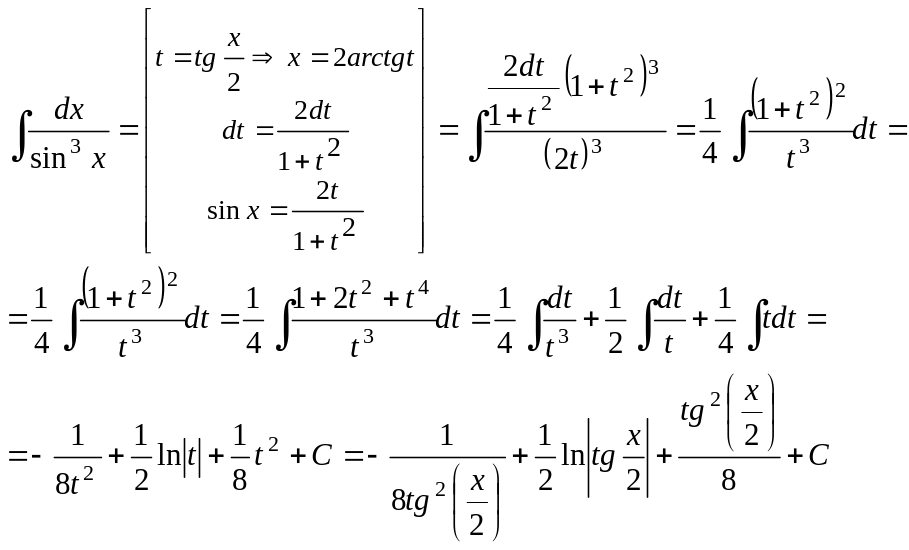
Ответ:

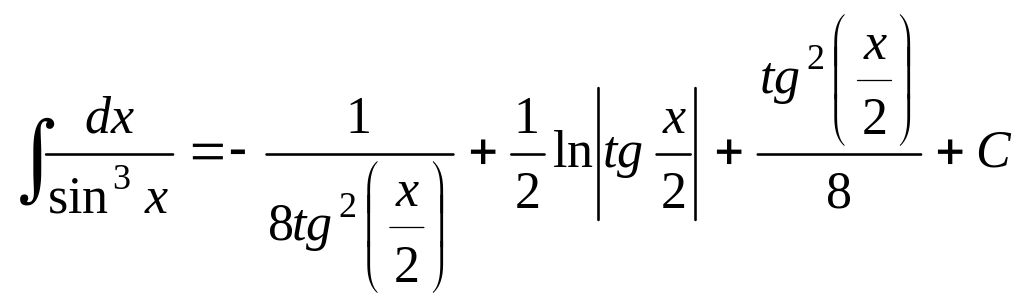
4) Интегралы вида , где f(u;V) – рациональная функция двух переменных.

Такие интегралы находят сведением к интегралу от рациональной дроби с помощью замены:

;

Пример 30.

Ответ:

5) Интегралы вида ; , где

Такие интегралы находят после предварительного применения формул:

;

Или с помощью замены:

;

или .

Пример 31.

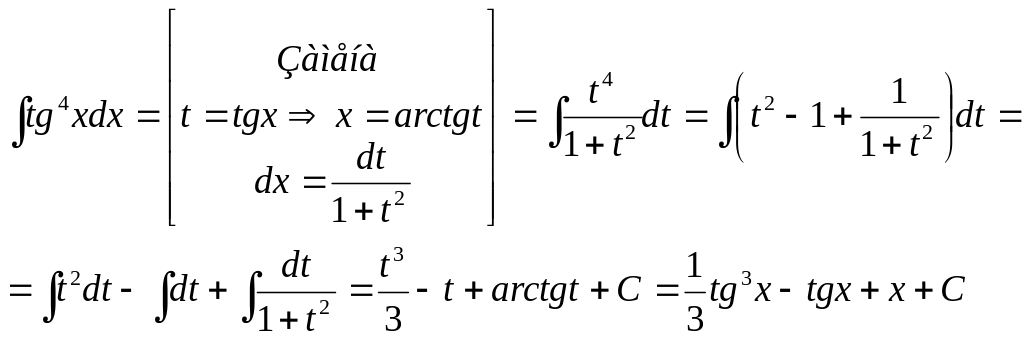
Ответ:

6. Интегрирование некоторых видов иррациональных выражений

1) Интеграл вида

Такие интегралы находят с помощью преобразований и замены, аналогичным преобразованиям и замены для нахождения интеграла от простой рациональной дроби III типа.

Пример 32.

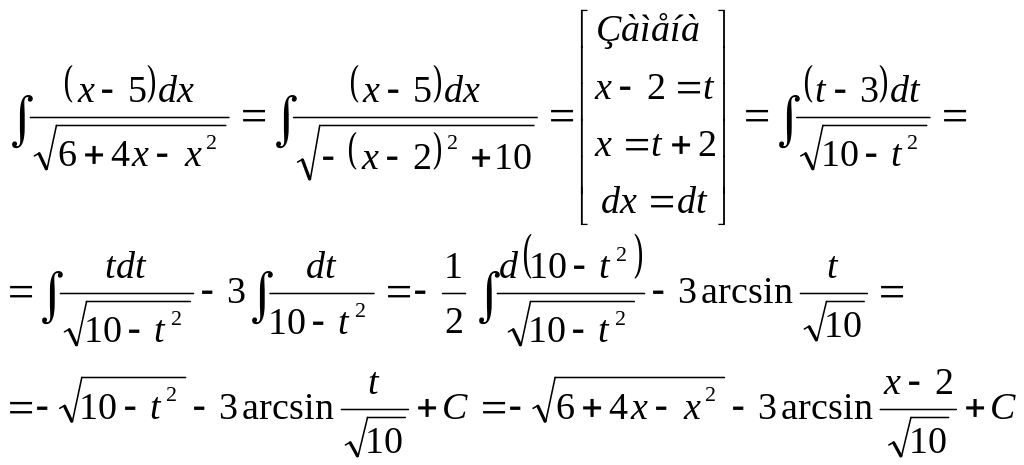
Ответ:

2) Подынтегральная функция содержит .

Тогда надо выполнить замену:

Такая замена приводит интеграл от некоторого тригонометрического выражения.

Пример 33.

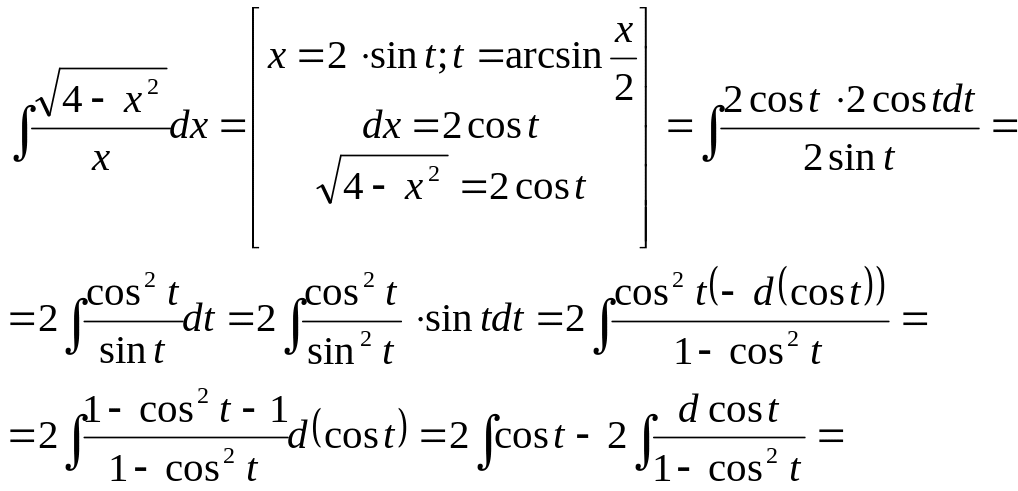
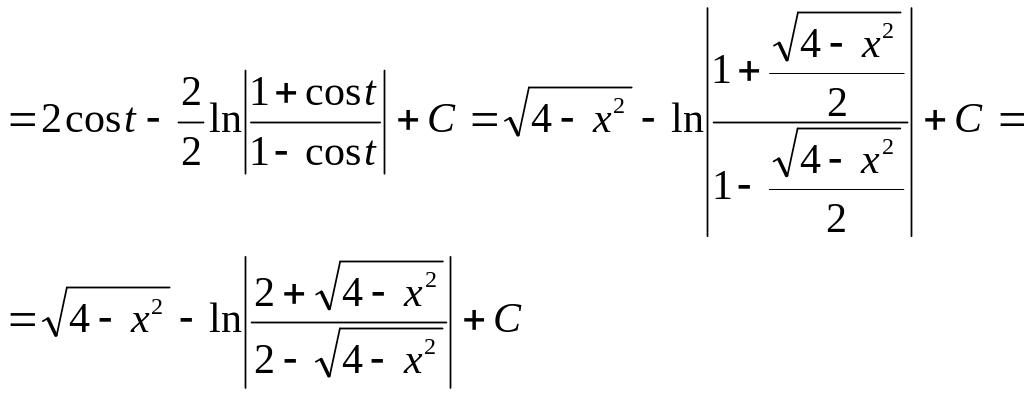
Ответ:

3) Подынтегральная функция содержит .

Тогда надо выполнить замену:

Пример 34.

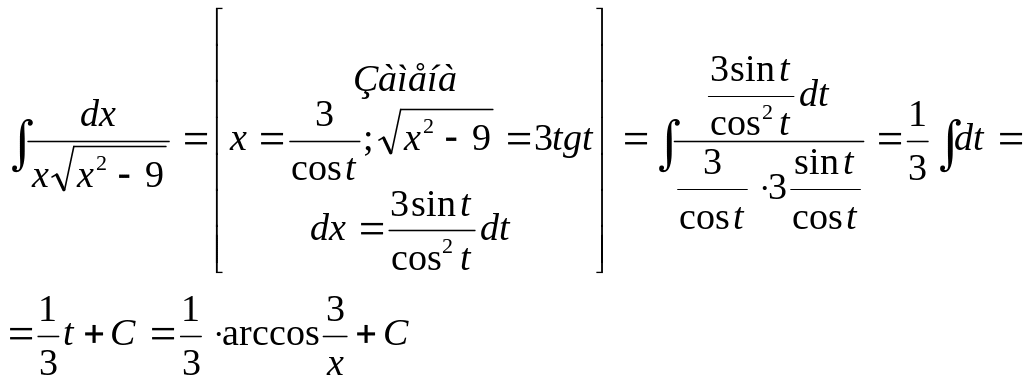
Ответ:

4) Подынтегральная функция содержит .

Тогда надо выполнить замену:

Пример 35.

Ответ:

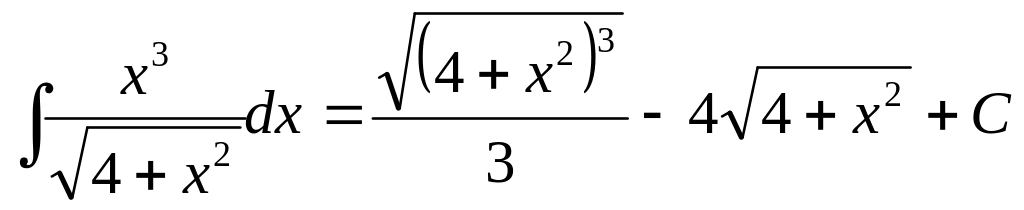
5) Подынтегральная функция содержит :

Тогда надо выполнить замену:

.

Пример 36.

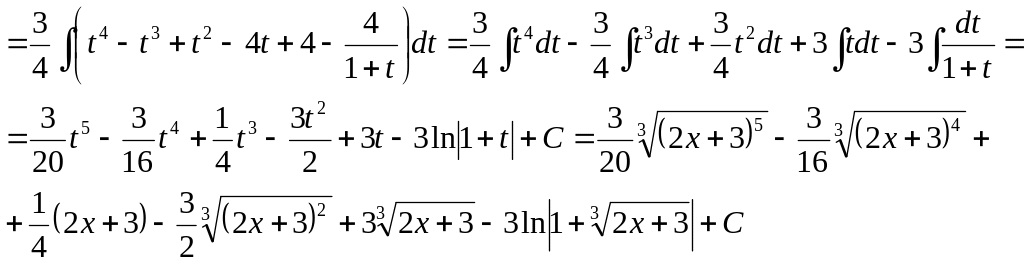
Ответ:

Пример 37.

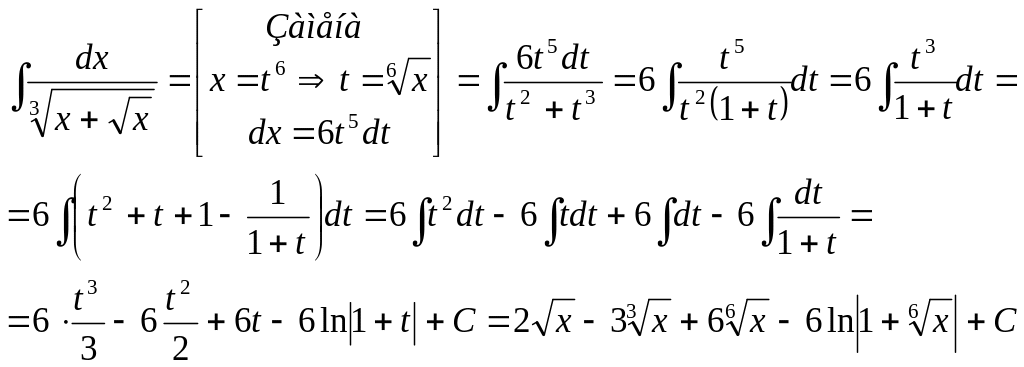
Ответ: