5) Интегрирование по частям в определенном интеграле
Теорема 6. Пусть функции u(x) и V(x) имеют непрерывные производные на [a;b]. Тогда справедливо равенство:
Доказательство.
Так как (u(x) V(x))' = u(x) V' (x) + u' (x) V(x) для любого x [a;b], то функция u(x) V(x) является одной из первообразных функции
u (x)V' (x) + u' (x) V(x).
Поэтому по формуле Ньютона-Лейбница:
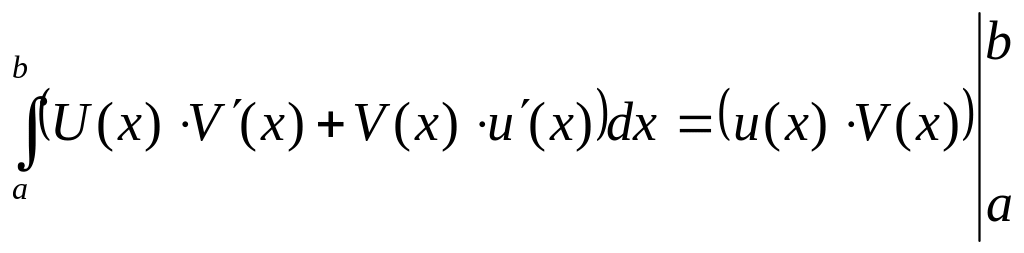
Пользуясь свойством определенного интеграла можно это равенство записать в виде:
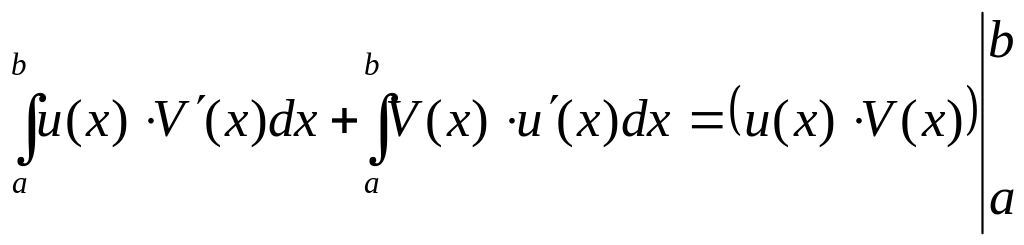
Отсюда следует:
Эту формулу удобно записать в виде:
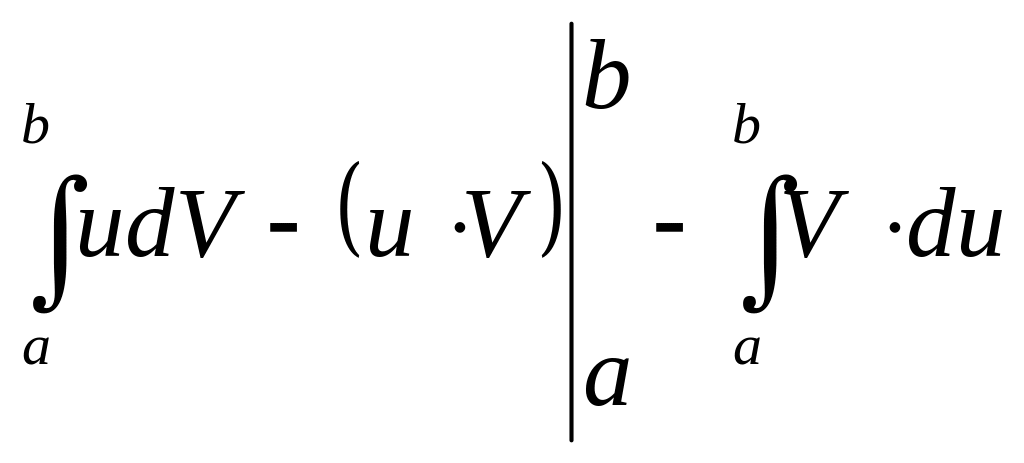
Пример 5.
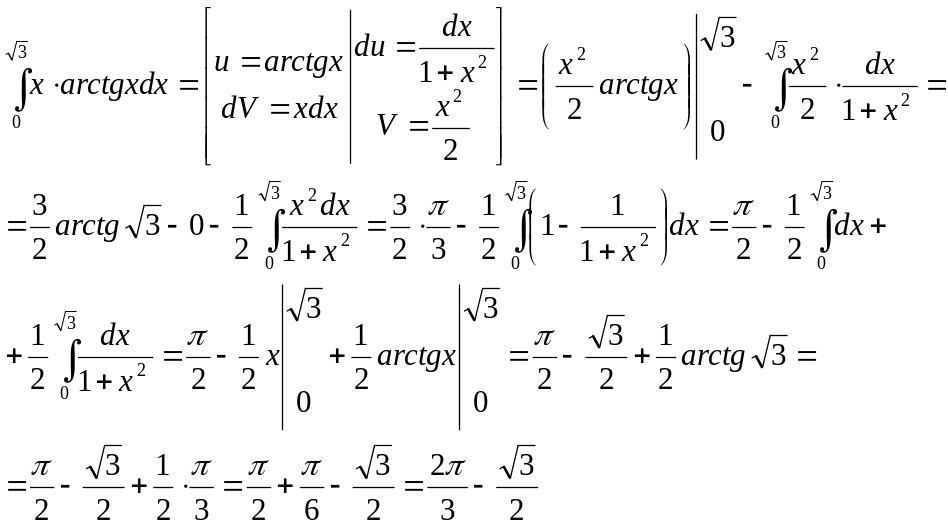
Ответ:
Пример 6.
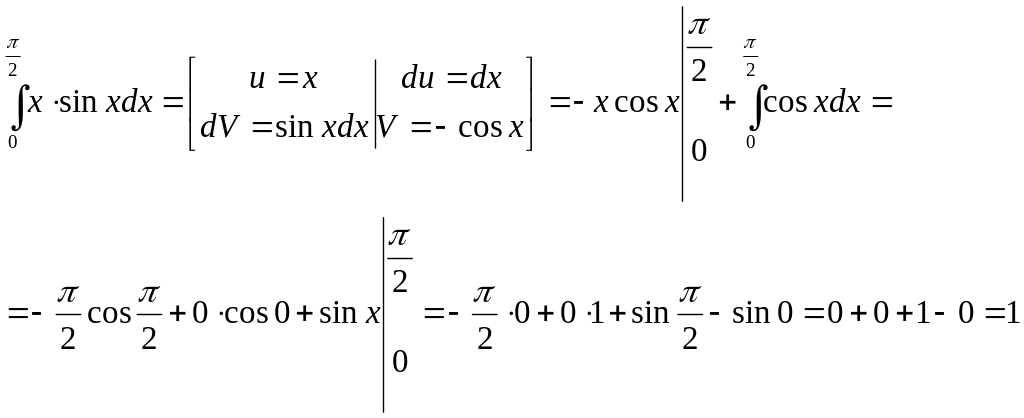
Ответ:
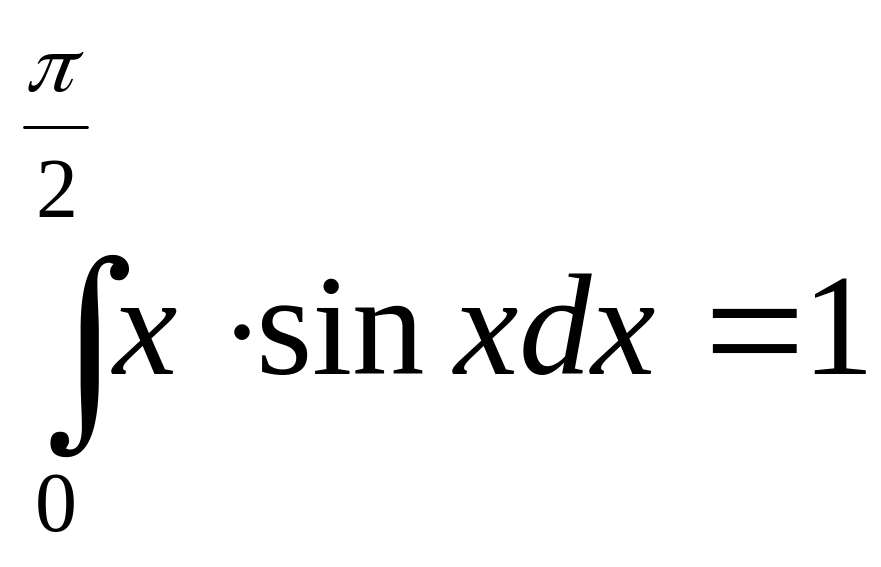
5. Приложения определенного интеграла
1) Вычисление площадей плоских фигур в прямоугольной системе координат
а) Область D ограничена кривыми y = f (x) и y = g (x), прямыми x=a и x=b, причем f(x) g(x) для xÎ [a;b].
.
б) Область D ограничена кривыми x = f (y) и x = g (y), прямыми y=c и y=d, причем f (y) g(y) для yÎ [c;d].
.
2) Вычисление площади плоской фигуры в полярной системе координат
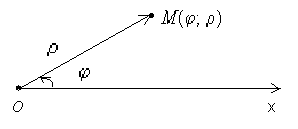
а) Полярная система координат задается полярной осью Ox, полюсом – точка O и масштабной единицей (рис.14)
Рис.14
Точка M в этой системе задается двумя координатами:
а)
- угол наклона
радиуса-вектора
к
оси Ox;
б)
- длина
.
Формулы перехода от полярной системы координат к прямоугольной системе, связанной с полярной точкой начала координат – т. O, осью абсцисс с полярной осью, а осью ординат, перпендикулярной полярной оси,
M(j;r)
= M(x;
y):
и
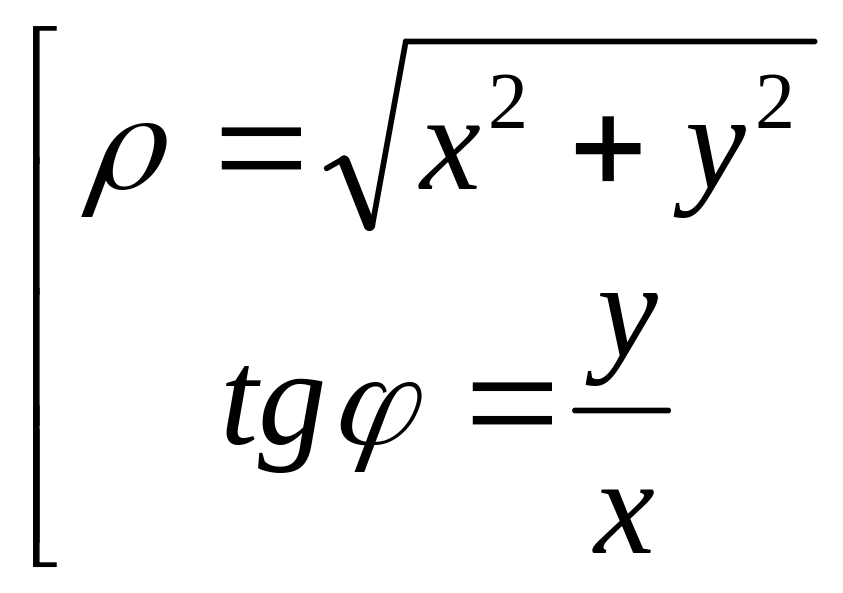
Уравнение кривой в полярной системе координат – соотношение между r и j : r = r (j).
Б) Площадь криволинейного сектора в полярной системе, ограниченного лучами j = и j = , кривой r = r(j) (рис.15), вычисляется по формуле:
.
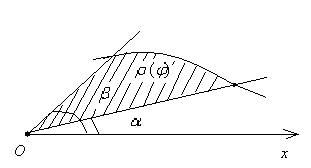
Рис.15
3) Вычисление объема тела по площадям параллельных сечений.
Пусть задано объемное тело T , для которого известна площадь S(x) любого сечения плоскостью, проходящей через точку (x;0;0) перпендикулярно оси Ox, a x b (рис.16).
Рис. 16
Пусть функция S(x) непрерывна на [a;b]. Тогда объем тела T вычисляется по формуле:
.
4) Вычисление объема тела вращения
а) Пусть надо вычислить объем тела, образованного вращением вокруг оси Ox криволинейной трапеции ABCD, ограниченной кривой y = f (x), осью Ox и прямыми x=a, x=b.
В таком случае площадь поперечного сечения в т. xÎ [a;b] круг радиусом f(x) равна:
.
Тогда объем тела, образованного вращением вокруг оси Ox этой криволинейной трапеции, вычисляется по формуле:
.
б) Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой x = (y), осью Oy и прямыми y = c, y = d, вычисляется по формуле:
.
§ 9. Несобственные интегралы
Изучая определенный интеграл от функции f (x), мы требовали, чтобы f (x) удовлетворяла следующим условиям:
1) была определена на конечном отрезке [a;b];
2) была непрерывна на отрезке [a;b].
Если нарушено одно из указанных условий, то речь будет идти о несобственных интегралах первого и второго рода.