
- •Математический анализ (1 семестр)
- •§ 1. Функция одной переменной, основные понятия
- •2. Способы задания функции
- •3. Сложная и обратная функции
- •4. Элементарные функции
- •4.1 Основные элементарные функции:
- •§ 2. Предел функции
- •Предел функции в конечной точке x0
- •Односторонние пределы
- •Предел функции на бесконечности
- •Бесконечно малые и бесконечно большие функции
- •5. Теоремы о конечных пределах
- •7. Второй замечательный предел
- •§ 3. Непрерывность функции
- •1. Непрерывность функции в точке и на промежутке
- •2. Теоремы о непрерывных функциях
- •3. Точки разрыва функции и их классификация
- •§ 5. Дифференцирование функции одной переменной
- •1. Определение производной, ее геометрический и механический смысл
- •2. Таблица производных основных элементарных функций
- •3. Дифференцируемость функции. Связь дифференцируемости с существованием производной и непрерывностью функции
- •4. Правила дифференцирования
- •5. Дифференциал функции
- •6. Производные и дифференциалы высших порядков
- •§ 5. Свойства функций, непрерывных на отрезке
- •§ 6. Исследование поведения функций
- •1. Асимптоты плоской кривой
- •2. Монотонность функции
- •3. Экстремумы функции
- •4. Выпуклость, вогнутость и точки перегиба графика функции
- •5. Наибольшее и наименьшее значение функции на отрезке
- •6. Схема исследования функции. Построение графика
- •Глава 2. Интегрирование
- •§ 7. Неопределенный интеграл
- •1. Первообразная функция и ее свойства
- •2. Понятие неопределенного интеграла
- •3. Свойства неопределенного интеграла.
- •4. Таблица основных неопределенных интегралов.
- •§ 8 Методы интегрирования
- •1. Непосредственное интегрирование
- •2. Интегрирование подстановкой.
- •3. Интегрирование по частям.
- •4. Интегрирование рациональных дробей
- •2. Интегрирование рациональных дробей
- •5. Интегрирование тригонометрических выражений
- •6. Интегрирование некоторых видов иррациональных выражений
- •§ 8. Определенный интеграл.
- •1. Задача, приводящая к определенному интегралу.
- •3. Свойства определенного интеграла.
- •4. Вычисление определенного интеграла
- •1) Интеграл с переменным верхним и постоянным нижним пределами и его свойства
- •2) Формула Ньютона-Лейбница
- •3) Вычисление определенного интеграла с помощью формулы Ньютона-Лейбница
- •4) Замена переменной в определенном интеграле
- •5) Интегрирование по частям в определенном интеграле
- •5. Приложения определенного интеграла
- •1) Вычисление площадей плоских фигур в прямоугольной системе координат
- •2) Вычисление площади плоской фигуры в полярной системе координат
- •3) Вычисление объема тела по площадям параллельных сечений.
- •4) Вычисление объема тела вращения
- •§ 9. Несобственные интегралы
- •1. Интегралы с бесконечными пределами
- •2. Интегралы от разрывных функций
§ 5. Дифференцирование функции одной переменной
1. Определение производной, ее геометрический и механический смысл
Пусть дана функция y = f(x), определенная на множестве D(f). Рассмотрим точку xD(f) и некоторое число x такое, чтобы точка x+xD(f). Это число Dx называется приращением аргумента x.
Определение 1. Приращением функции y = f(x) называется разность f(x+Dx) - f(x). Приращение функции y = f(x) обозначают Dy. То есть Dy = f(x+Dx) - f(x).
Определение 2.
Производной
функции y
= f(x)
называется предел отношения приращения
функции Dy
к приращению аргумента Dx,
если приращение аргумента Dx
стремится к нулю и этот предел существует.
Производную функции y
= f(x)
обозначают:
![]() или
или
![]() .
Поэтому можно записать:
.
Поэтому можно записать:
![]()
Пример. Исходя из определения, найти производную функции у = .
Решение. Dy=
f(x+
Dx)
- f(x)
= =![]() .
.
![]() .
.
Ответ:
![]()
![]()
Механический смысл производной
Пусть материальная точка движется по прямой по закону S=S(t):
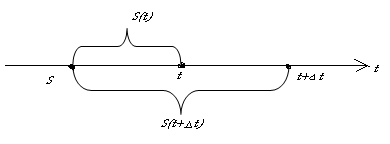
Тогда DS = S(t+Dt) – S(t) – расстояние, пройденное за время Dt. Тогда средняя скорость движения:
Vcр
=
![]() .
.
Чтобы найти скорость движения в момент времени t, надо рассмотреть предел Vcр при Dt 0:
V(t)
=
![]() .
.
Значит, производная от пути S(t) равна мгновенной скорости точки в момент времени t:
![]() .
.
Геометрический смысл производной
Рассмотрим график функции y = f(x) в окрестности фиксированной точки x0 (рис.5).

Рис. 5
Точка M0(x0;y(x0)) – фиксированная точка графика y = f(x). Точка M(x0+Dx;y(x0+Dx)) при различных значениях Dx – любая точка на графике. Если точка M приближается к точке M0 (при этом Dx 0), то секущая линия M0M стремится к своему предельному положению, называемому касательной к линии y = f(x) в точке M0.
Рассмотрим
M0MA:
tgсек=
![]() ,
сек
= угол наклона секущей M0M
к оси Ox.
,
сек
= угол наклона секущей M0M
к оси Ox.
Перейдем к пределу при Dx 0:
![]()
То есть y' (x0) = tg кас => частное значение производной функции y = f(x) в точке x0 равно угловому коэффициенту касательной, проведенной к линии y = f(x) в точке M0(x0;y(x0)).
Тогда, используя уравнение прямой, проходящей через заданную точку M0(x0;y0) с известным угловым коэффициентом Kкас = y'(x0), можно записать уравнение касательной к линии y = f(x) в точке M0(x0;f(x0)):
y = f(x0) + f' '(x0) × (x-x0)
Аналогично, можно записать уравнение нормали – прямой, перпендикулярной касательной и проходящей через точку касания M0(x0;f(x0)):
y
= f(x0)
-
![]() ,
,
используя условие
перпендикулярности прямых: Kнорм
= -![]() .
.
2. Таблица производных основных элементарных функций
1)
![]()
Вывод:
![]() ;
;
![]()
![]()

2)
![]() ;
;
Вывод:
![]() ;
;
![]()
![]()
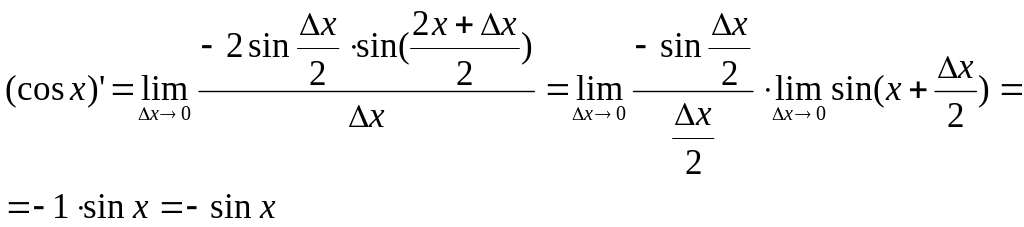
3)
![]()
Вывод:
![]() ;
;
![]()
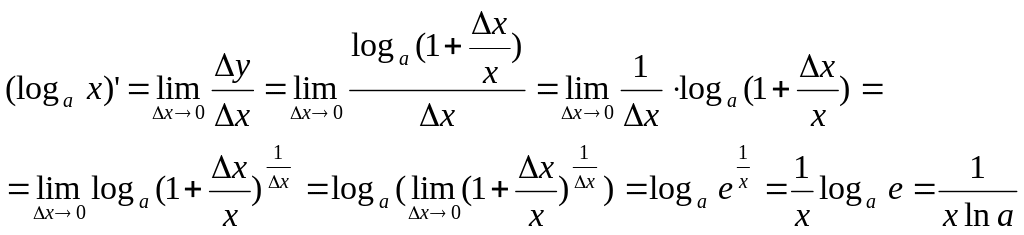
(используется второй замечательный предел и свойства логарифма).
4)
![]()
Вывод: так как ln
x
= loge
x,
то, используя производную, для (loga
x),
можно записать:
![]()
5) (c)' = 0
Вывод: y
= c,
y
= y(x+x)
- y(x)
= c-c
= 0
![]()
Для остальных функций производные выводятся позже с помощью правил дифференцирования.
Таблица производных основных элементарных функций
(c)' =0
(x) = x-1
(ax)' = axlna, (a>0, a 1)
(ex)' = ex
(logax)' =
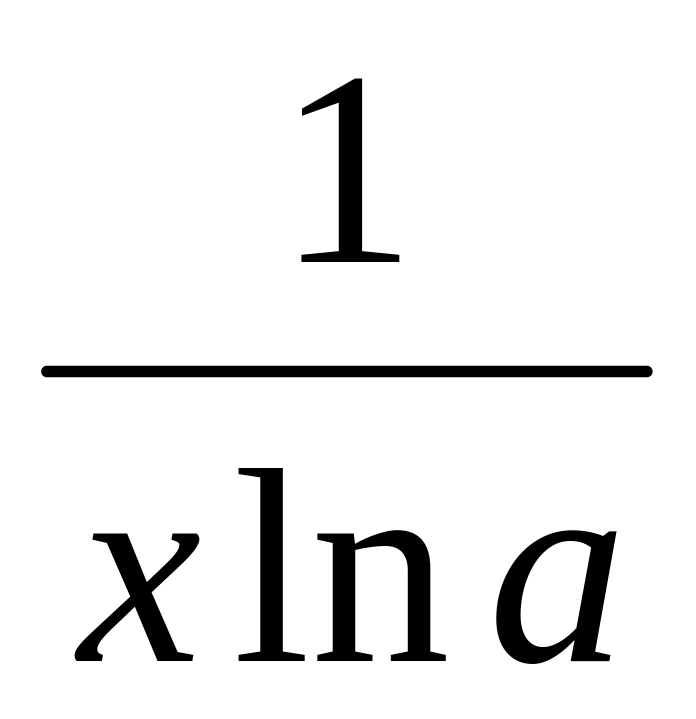 ,
(a>0;
a
1)
,
(a>0;
a
1)(lnx)' =
(sinx)' =cosx
(cosx)' = - sinx
(tgx)' =
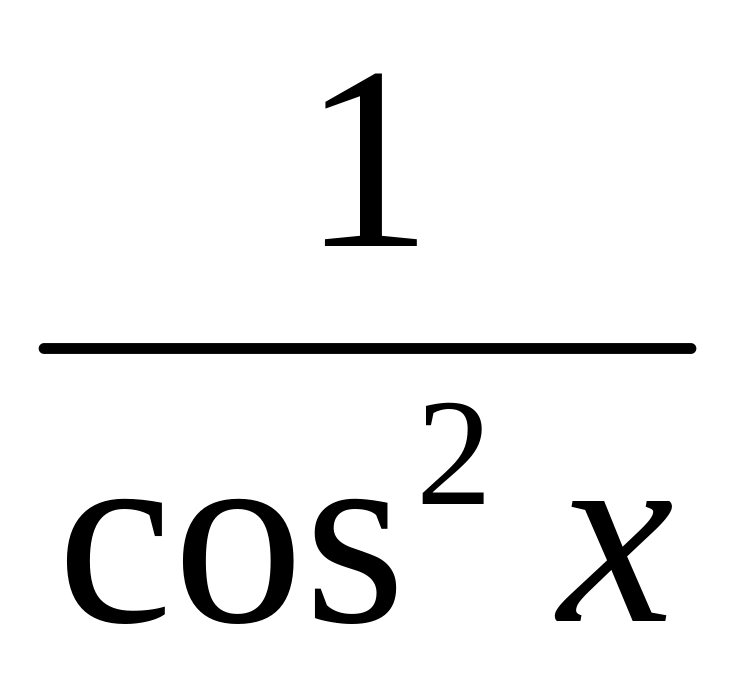
(ctgx)' = -
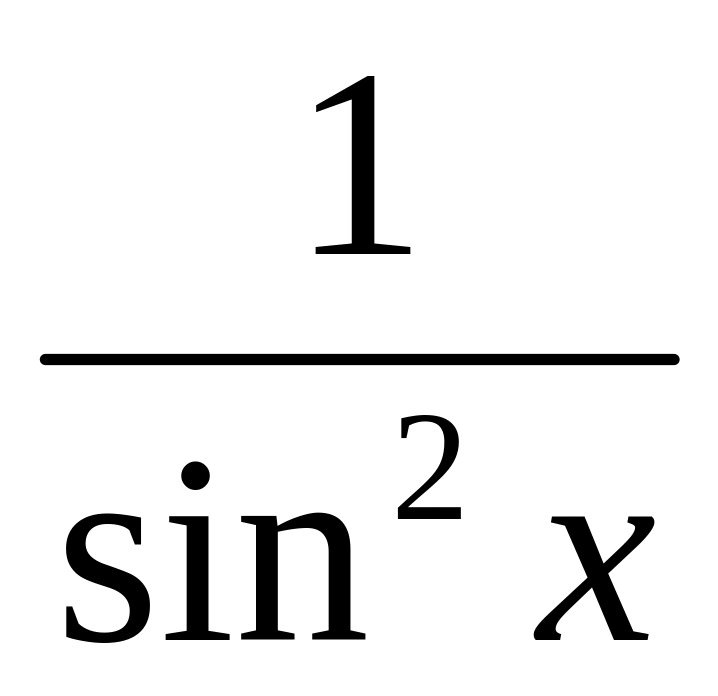
(arcsinx)' =
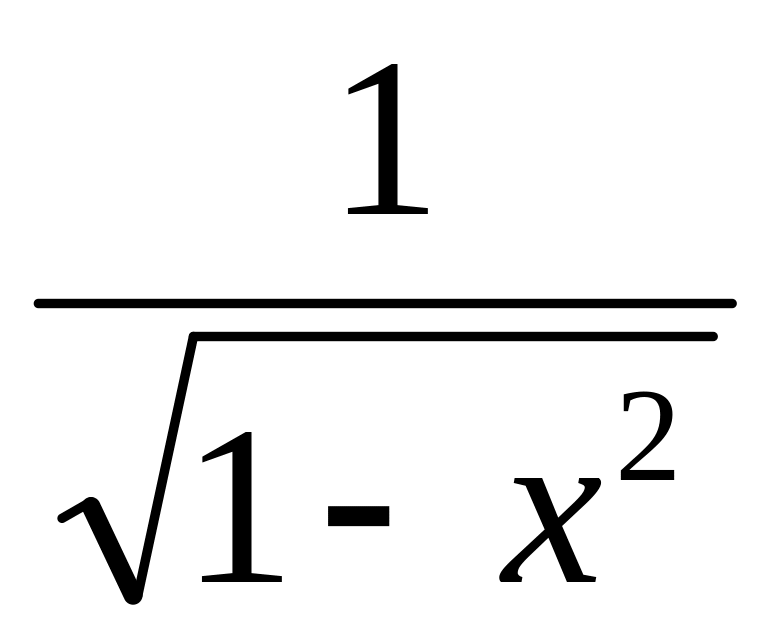
(arccosx)' = -
(arctgx)' =
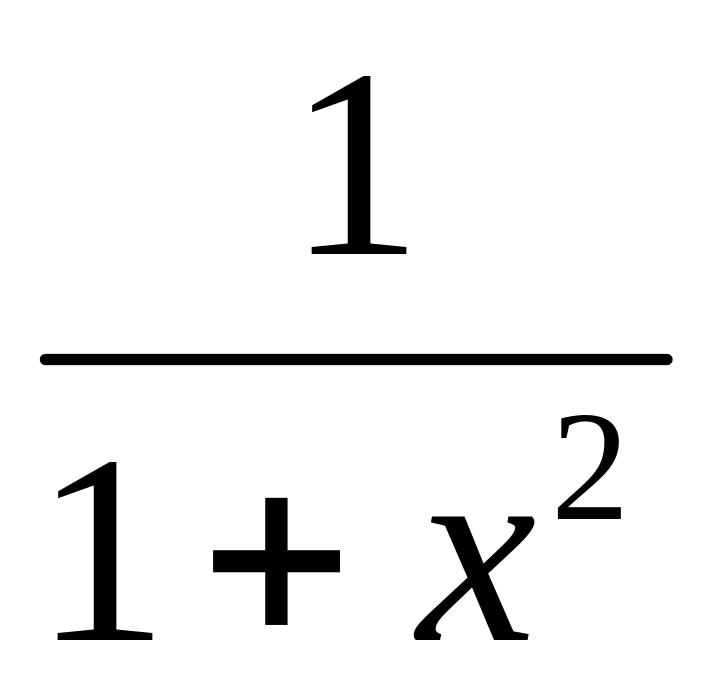
(arcctgx)' = -
