4. Вычисление определенного интеграла
1) Интеграл с переменным верхним и постоянным нижним пределами и его свойства
Определение 4.
Пусть функция y
= f
(x)
непрерывна на [a;b].
Тогда она непрерывна на [a;x]
для любого x
[a;b].
Следовательно, на [a;b]
определена функция
,
которая называется интегралом
с переменным верхним пределом.
Свойства этой функции сформулируем в виде теоремы.
Теорема 3.
Пусть функция f
(x)
непрерывна на [a;b].
Тогда функция
обладает свойствами:
1) непрерывна на [a;b];
2) имеет производную
F'
(x)
в каждой точке x
[a;b],
удовлетворяющую равенству
.
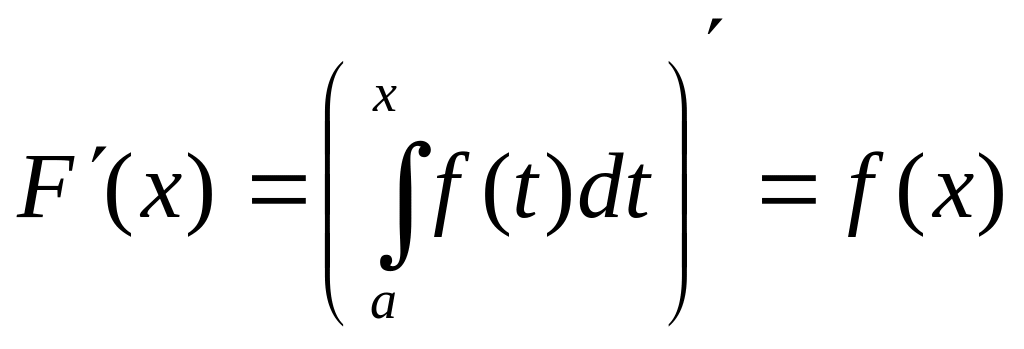Доказательство: Вычислим приращение функции F (x), причем D x возьмем таким, чтобы точка x + D x [a;b].
Тогда
Применим к полученному интегралу теорему о среднем значении определенного интеграла. То есть на [x; x + Dx] существует такое число c, в котором выполняется равенство:
Значит, F = f (c) Dx, где c [x; x + Dx].
Если Dx 0, то c x (так как x < c < x+Dx).
Поэтому, в силу непрерывности f (x), получим f (c) f (x) при Dx0.
Таким образом, DF0 при Dx0, что доказывает непрерывность F (x).
Кроме того, вычисляя предел отношения DF к Dx при Dx 0, получим:
То есть существует конечный предел отношения DF к Dx при Dx0. Что означает существование производной F' (x) = f (x).
Из этой теоремы следует, что функция является первообразной для функции f (x).
2) Формула Ньютона-Лейбница
Теорема 4. Пусть
функция f
(x)
непрерывна на [a;b]
и
(x)
– какая-либо ее первообразная на [a;b].
Тогда определенный интеграл от функции
f
(x)
по отрезку [a;b]
равен разности значений функции F(x)
в точках b
и
a:
Доказательство. Из теоремы 3 следует, что наряду с функцией F(x) функция также является на [a;b] первообразной для f (x). Тогда по свойству первообразных для одной и той же функции на некоторой области имеем:
для любого x
[a;b]
()
Вычислим значение
const.
Для этого, используя свойство 1
определенного интеграла
,
рассмотрим равенство ()
при x
= a:
Следовательно, равенство () можно переписать в виде:
для x
[a;b]
Теперь рассмотрим полученное равенство при x = b:
Это и есть формула Ньютона-Лейбница. Она является основной формулой интегрального исчисления, устанавливающей связь между определенным и неопределенным интегралами и дает правило вычисления определенного интеграла.
Замечание. Формулу Ньютона-Лейбница часто записывают в виде:
,
Где используется обозначение:
.
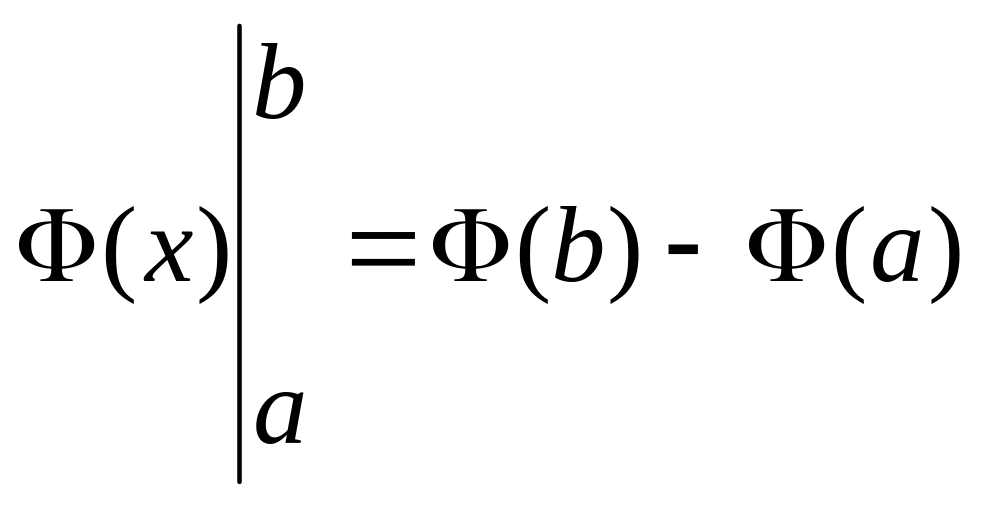3) Вычисление определенного интеграла с помощью формулы Ньютона-Лейбница
Задача вычисления определенного интеграла свелась к нахождению первообразной непрерывной функции.
Пример 1.
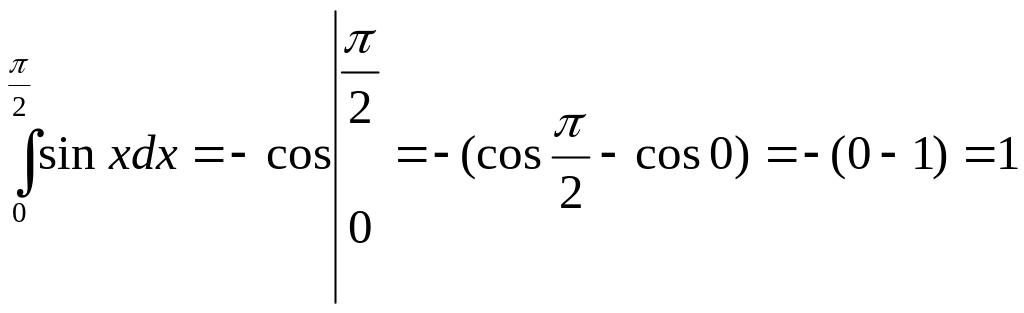
Ответ:
Пример 2.
Ответ:
4) Замена переменной в определенном интеграле
Теорема 5. Пусть функция f (x) непрерывна на отрезке [a;b] и пусть функция x = (t) имеет непрерывную производную j '(t) на отрезке [;], область значений этой функции – отрезок [a;b], то есть a j (t) b для x t [a;b], причем j (a) = a, j (b) = b.
Тогда справедливо равенство:
.
Доказательство. Так как f (x)непрерывна на [a;b], то существует определенный интеграл и справедлива формула Ньютона-Лейбница:
(1)
где F(x) – одна из первообразных f (x) на [a;b].
Известно, что F(x) дифференцируема в любой точке [a;b], причем
F'(x) = f (x) для любого x [a;b].
Так как функция x = j (t) непрерывна на [a;b] и множество ее значений совпадает с отрезком [a;b], то сложные функции f(j(t)) и F(j(t)) непрерывны в любой точке t Î [a;b].
Так как j ' (t) непрерывна на [a;b], то функция f(j(t)) j ' (t) тоже непрерывна на [a;b], а значит существует интеграл:
.
Покажем, что функция
F(j(t))
является первообразной для
.
Действительно,
(F(j
(t)))'t
= F'(x)
j
'(t)
= f
(x)
j'
(t)
= f
(j
(t))
j'
(t)
для любого t
Î
[a;b].
Поэтому можно к этому интегралу применить
формулу Ньютона-Лейбница:
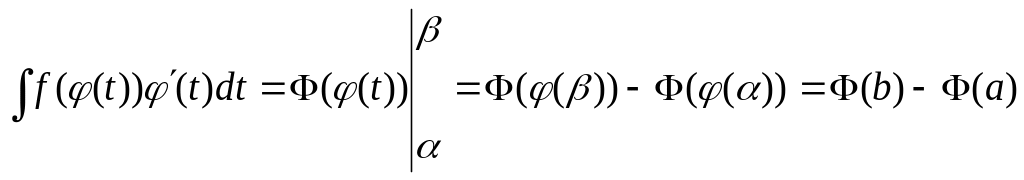
(так как j (b) = b и j (a) = a). (2)
Сравнивая результаты (1) и (2) приходим к равенству:
.
Пример 3.
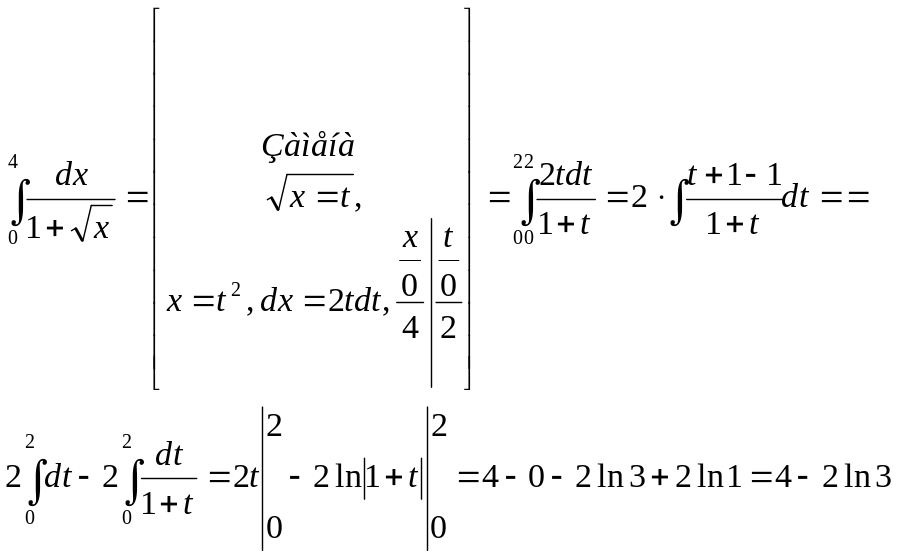
Ответ:
Пример 4.
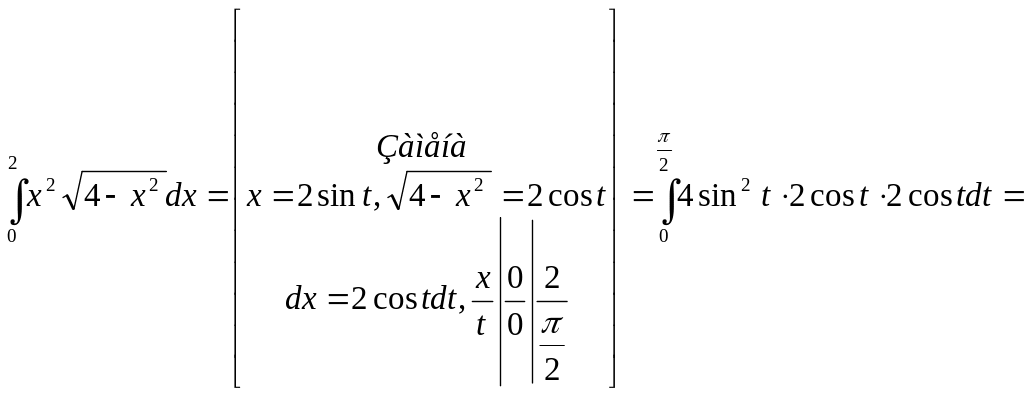
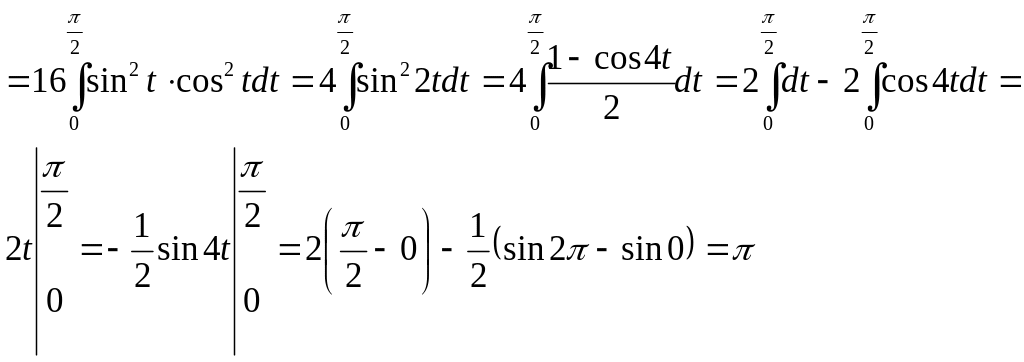
Ответ:
