§ 8. Определенный интеграл.

1. Задача, приводящая к определенному интегралу.

Пусть на [a;b] задана непрерывная неотрицательная функция y = f (x).

Определение 1. Криволинейной трапецией называется фигура, ограниченная осью абсцисс прямыми x = a, x = b и графиком функции y = f(x).

Ставится задача: вычислить площадь этой криволинейной трапеции (рис.13)

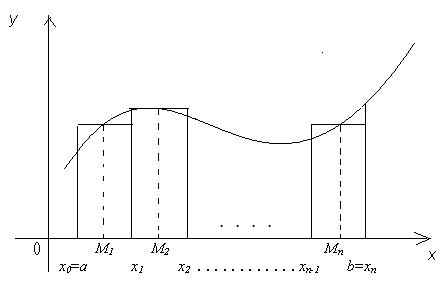
Рис.13

Решение.

1) Разобьем отрезок [a;b] на n частей точками x₀ = a; x₁; x₂; x_n-1; x_n = b и проведем прямые x = x₁, x = x₂, … x = x_т-1, которые разобьют трапецию на n частей.

2) Обозначим  x_k = x_k - x_k-1 – длины отрезков разбиения [a;b]. На каждом их отрезков произвольно выберем точку M_k (k = 1;… n).

Построим на каждом из отрезков прямоугольники с высотами, равными значению функции в выбранных точках M_k .

Площади полученных прямоугольников равны: S₁ = f (M₁)  D x₁; S₂ = f (M₂)  D x₂; ….; S_n = f (M_n)  D x_n .

3) Найдем сумму этих площадей:

Получили площадь ступенчатой фигуры. Эта площадь зависит от способа разбиения отрезка [a;b] на части и от выбора на каждой из частей точек M_k (k = 1;… n).

Чем больше будет точек разбиения [a;b] на части и мельче по длине эти части, тем точнее сумма будет приближаться к площади данной криволинейной трапеции. То есть можно записать:

Определение 2. Сумма называется интегральной суммой функции f (x) на отрезке [a;b].

Определение 3. Предел интегральной суммы S функции f (x) на [a;b] при n   и max D x_k  0 называется определенным интегралом функции f (x) на отрезке [a;b], если этот предел существует и не зависит ни от способа разбиения [a;b] на части, ни от выбора точек M_k (k = 1;… n) на каждой из частей. Следовательно, можно записать:

.

При этом отрезок [a;b] называют отрезком интегрирования, “a” – нижним пределом интегрирования, “b” – верхним пределом.

Теорема 1 (достаточное условие интегрируемости функции на [a;b])

Если функция f (x) на [a;b] непрерывна, то определенный интеграл существует, то есть функция f (x) на [a;b] интегрируема.

2. Геометрический смысл определенного интеграла

1)

.

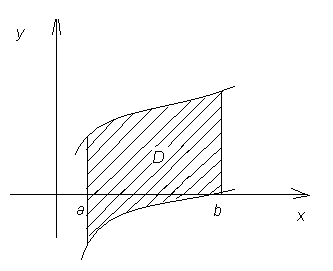
2) Если область ограничена двумя кривыми y = f (x) и y = g (x), причем при x [a;b] f (x)  g (x), то площадь области ограниченным кривыми y = f (x); y = g (x) и прямыми x = a, x = b вычисляется по формуле:

3. Свойства определенного интеграла.

1)

2)

3)

4)

5) Если функция f (x) интегрируема на отрезках [a;c] и [c;b], то она интегрируема и на [a;b], причем верно равенство:

При любом расположении точек a, b и c на оси Ox.

6) Если f (x)  0 при x [a;b], то

7) Если на [a;b] f (x)  g (x), то

8) Теорема 2 (о среднем значении определенного интеграла).

Если функция f (x) непрерывна на [a;b], то на этом отрезке найдется хотя бы одна точка c, в которой выполняется равенство:

Доказательство: Так как f (x) на [a;b] непрерывна, то она достигает на этом отрезке своих наименьшего “m” и наибольшего “M” значений. Тогда m  f (x)  M для любого x  [a;b]. По свойству 7 определенного интеграла можно записать неравенство:

Так как m и M – постоянные числа, то

()

Вычислим по определению определенного интеграла

Тогда неравенство () можно переписать:

Разделим все части полученного неравенства на (b - a) > 0 (длина отрезка интегрирования):

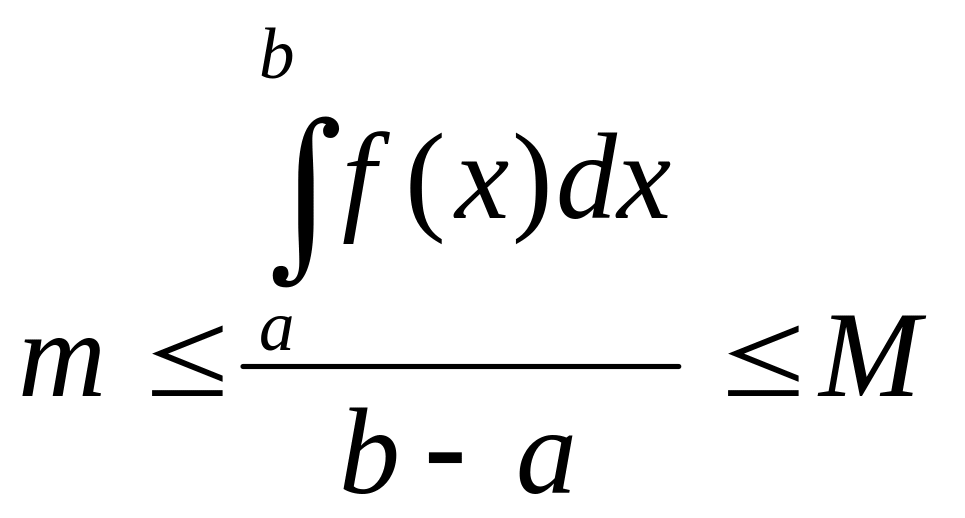
Так как f (x) непрерывна на [a;b], тона принимает все значения, заключенные между наименьшим “m” и наибольшим “M” значениями. Значит найдется на [a;b] хотя бы одна точка c, в которой выполняется равенство:
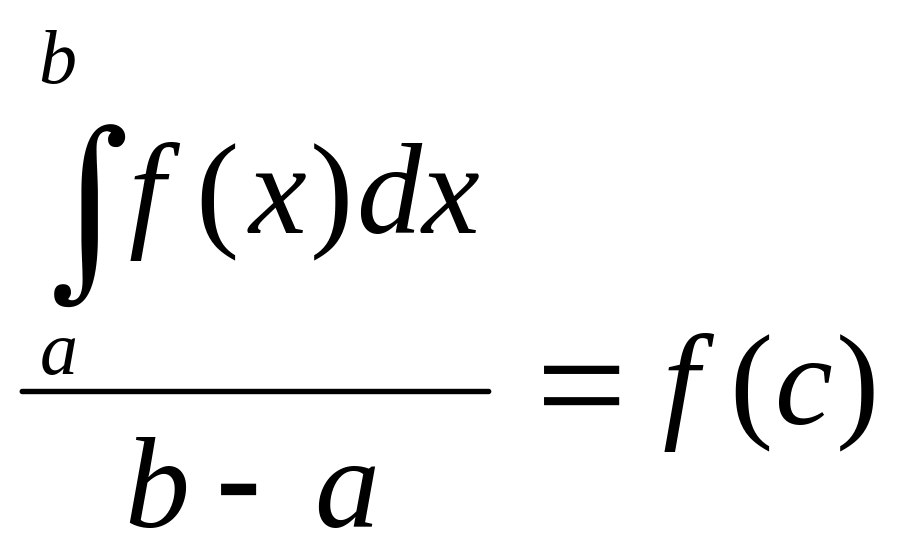