3. Интегрирование по частям.
Метод интегрирования по частям базируется на следующей теореме:
Теорема 2. Пусть функция U = U(x) и V = V(x) дифференцируемы на некотором интервале (a;b). Пусть на (a;b) функция V(x)U’(x) имеет первообразную. Тогда на (a;b) функция U(x)V’(x) также имеет первообразную. При этом справедливо равенство:
.
Доказательство. По форме дифференцирования:
(U(x)V(x))’ = U’(x)V(x) + U(x)V’(x).
По свойству неопределенного интеграла:
.
Тогда можно записать:
Замечание 1. Определение дифференциала и свойства инвариантности его формы позволяют переписать формулу интегрирования по частям в более короткой форме:
.
Замечание 2.
Для успешного вычисления интеграла
необходимо разумно разбить подинтегральное
выражение на два множителя u(x)
и dV(x)
так, чтобы интеграл
оказался легко интегрируемым.
Практика показывает, что большая часть интегралов, берущихся с помощью метода интегрирования по частям может быть разбита на следующие три группы.
1) К первой группе относятся интегралы, у которых подынтегральная функция содержит в качестве множителя одну из следующих функций:
Ln x; arcsin x; arcos x; arctg x; arcctg x; ln2x; ln(x); arcsin2x;…
при условии, что оставшаяся часть подынтегральной функции представляет собой производную известной функции.
Тогда за функцию u(x) берут соответствующую из перечисленных.
2) Ко второй группе относятся интегралы вида
,
,
,
,
где a,b,, ,A – некоторые постоянные числа, A > 0, n N.
При этом в качестве u(x) следует брать (ax +b)n и интегрировать по частям n раз.
3) К третьей группе относятся интегралы вида:
,
,
,
,
,
,
где , , A – постоянные числа, A > 0, A 1.
Такие интегралы берутся двукратным интегрированием по частям при любом выборе u(x). Это приводит к линейному уравнению относительно предложенного интеграла, откуда его и находят.
Замечание. Указанные три группы не исчерпывают всех без исключения интегралов, берущихся методом интегрирования по частям.
Пример 14.
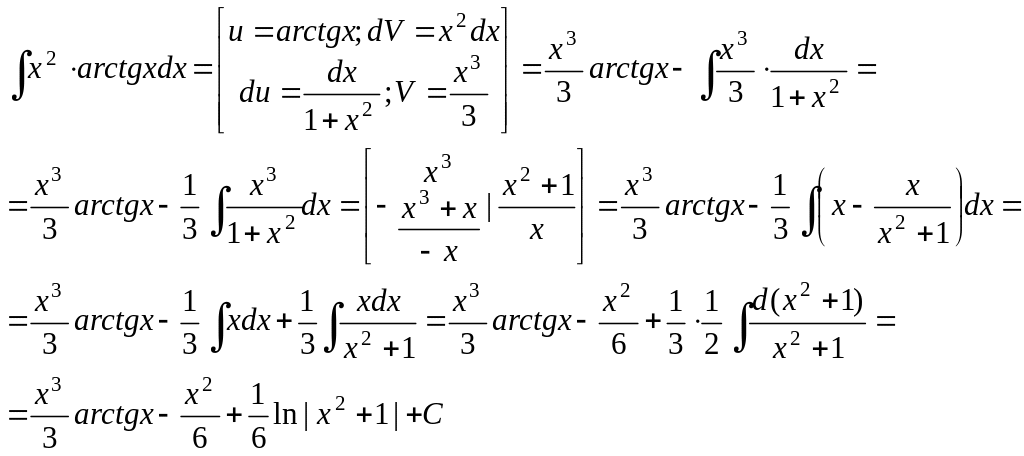Ответ:
Пример 15.
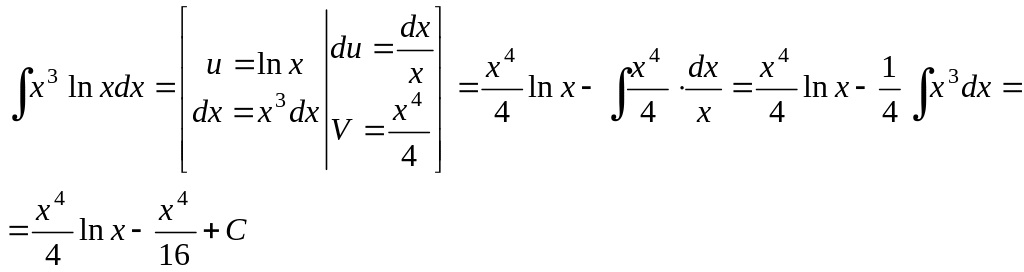
Ответ:
Пример 16.
Ответ:
Пример 17.
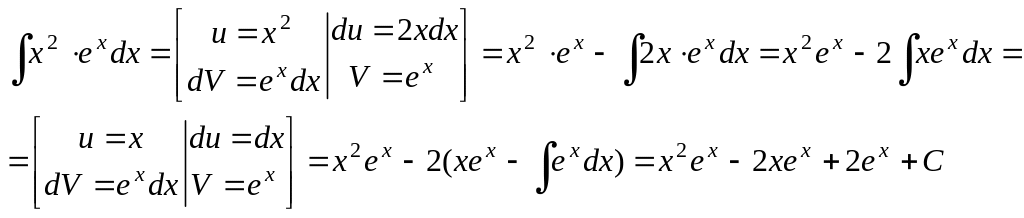Ответ:
Пример 18.
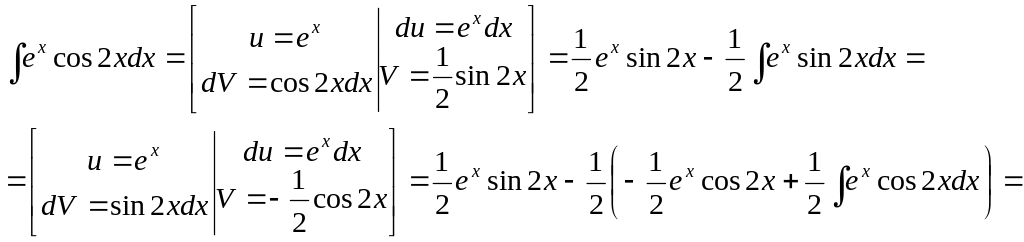
Далее необходимо решить уравнение:
Пусть
,
тогда уравнение запишется в виде:
Ответ:
Пример 19.
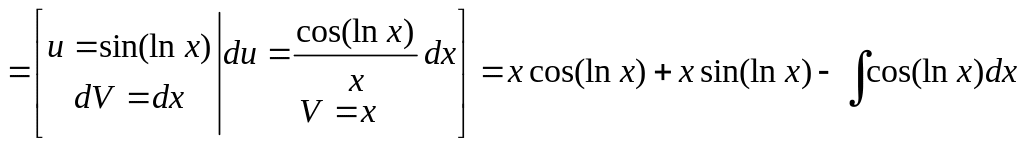
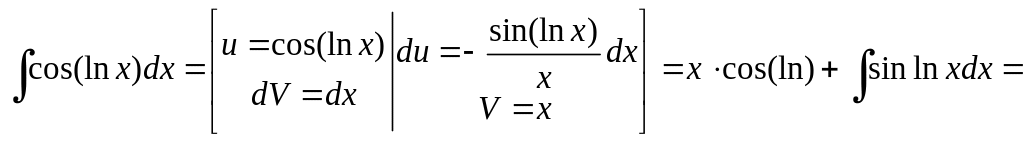
Пусть
,
тогда получили уравнение вида:
Ответ:
4. Интегрирование рациональных дробей
1) Разложение рациональной дроби на сумму простых дробей.
Определение 1. Рациональной дробью называется отношение двух многочленов:
Определение 2. Рациональная дробь называется правильной, если m<n. В противном случае (если m n) она называется неправильной.
Определение 3. Простыми рациональными дробями называются дроби следующих четырех типов:
I
.
II
.
III
IV
Теорема 3. Всякую неправильную рациональную дробь можно представить в виде суммы целой части (многочлена) и правильной рациональной дроби.
Пример 20.
Представить дробь
в виде суммы целой части и правильной
рациональной дроби.
Так как высшая степень числителя равна 4, а знаменателя – 2, то данная дробь неправильная (4 > 2). Разделим числитель на знаменатель:
Следовательно, дробь можно записать в виде:
.
Ответ:
.
Теорема 4. Любую правильную рациональную дробь можно единственным образом представить в виде суммы конечного числа простых рациональных дробей.
Разложение
правильной рациональной дроби
(m<n)
на сумму простых дробей выполняют по
следующей схеме:
а) Найти корни многочлена Qn(x) и представить его в виде произведения простых множителей:
,
Где
,
,
,
,
б) Записать разложение дроби с неопределенными коэффициентами:
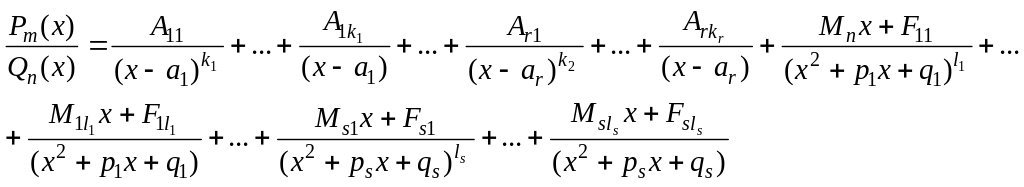
в) Определить коэффициенты
суммарное число которых равно n, методом неопределенных коэффициентов.
Для этого необходимо все разложение привести к общему знаменателю и приравнять числитель полученной дроби Pm(x). Приравнивания в этих многочленах коэффициенты при одинаковых степенях x, получим систему из n линейных уравнений с n неизвестными. Эта система имеет единственное решение – интересующие нас коэффициенты.
Пример 21.
Разложить дробь
на сумму простых дробей.
1) Данная дробь правильная. Разложим знаменатель на множители:
.
2) Запишем разложение данной дроби на сумму простых дробей:
3) Для нахождения коэффициентов A, B и C приводим разложение к общему знаменателю и приравняем их числители.
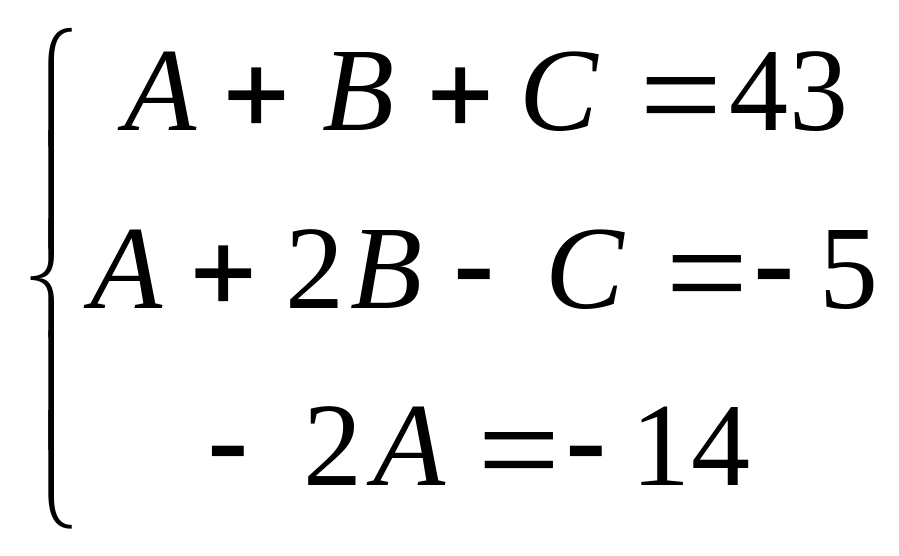
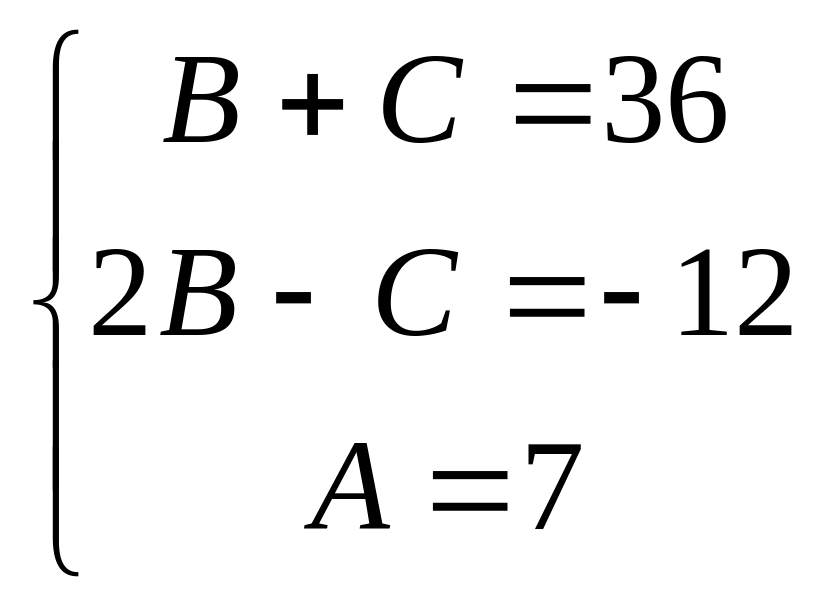
Следовательно:
