5. Теоремы о конечных пределах

Теорема 1. Функция f(x) имеет конечный предел в точке тогда и только тогда, когда выполняется равенство: f(x)=А+a(x), где a(x) – бесконечно малая функция в точке .

Доказательство этой теоремы вытекает из определения предела функции в точке и определения бесконечно малой функции в точке.

Теорема 2. Если существуют конечные пределы двух функций f(x) и g(x) в точке , то существует конечный предел суммы этих функций в точке , равный сумме пределов этих функций.

Доказательство: Пусть , тогда по теореме 1 f(x)=А+a(x), где a(x)– бесконечно малая функция в точке x₀.

Пусть, , тогда по теореме 1 g(x)=B+β(x), где β(x) – бесконечно малая функция в точке x₀. Рассмотрим сумму этих функций: f(x) + g(x) = = A + a(x) +B + β(x) = (A+B) + a(x) + β(x), обозначим γ(x) = a(x) + β(x) -

бесконечно малая функция в точке x₀ (по свойству 1 бесконечно малых функций). Получим f(x)+g(x)=A+B+γ(x).

По теореме 1: .

Теорема доказана.

Теорема 3. Если существуют конечные пределы двух функций f(x) и g(x) в точке , то существует предел произведения этих функций в точке , равный произведению пределов этих функций.

Доказательство: Пусть =А, тогда по теореме 1: f(x)=А+a(x), где a(x) – бесконечно малая функция в точке . Пусть , тогда по теореме 1: g(x) = B + β(x), где β(x) – бесконечно малая функция в точке . Рассмотрим произведение этих функций:

f(x) × g(x) = (А +a(x))(B + β(x)) = AB + B×a(x) + A×β(x) + a(x) ×β(x).

Обозначим: Ba(x) + Aβ(x) + a(x)β(x) = γ(x) – бесконечно малая функция в точке (по свойствам бесконечно малых функций). Получим: f(x)×g(x) = A×B + γ(x).

По теореме 1: .

Теорема доказана.

Теорема 4. Если существуют конечные пределы f(x) и g(x), причем , то существует предел частного этих функций в точке , равный частному пределов этих функций.

То есть: если существует =А и существует , B≠0, то существует .

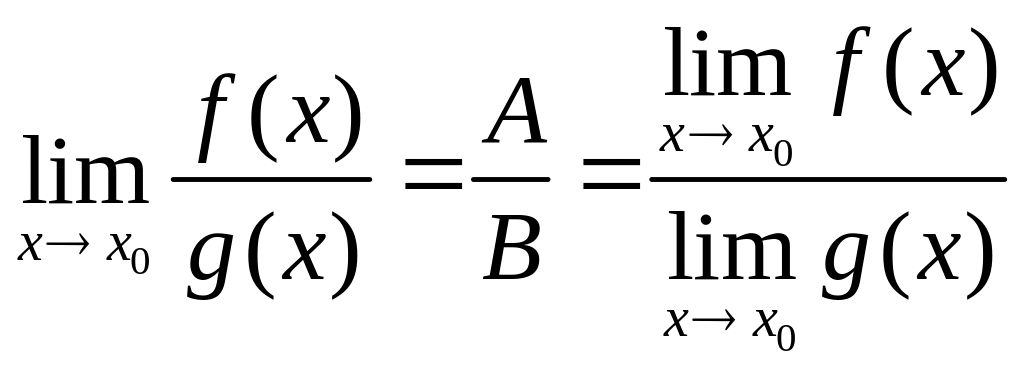(Доказать самостоятельно)

Теорема 5 (о пределе трех функций)

Если существуют равные конечные пределы функций f(x) и g(x) в точке :

= А

И при стремлении x к x₀ выполняется неравенство:

,

то существует .

Доказательство. Возьмем любое  > 0. Вычитая из всех частей двойного неравенства, данного в условии, число A, получим

()

Так как

,

то найдется такое ₁, что для всех x  x₀, удовлетворяющих условию

,

будет верно неравенство

,

или, что, то же,

()

Аналогично для функции g(x) найдется такое ₂, что для всех x  x₀, удовлетворяющих условию

будет верно неравенство

()

Из неравенств, отмеченных () следует, что

,

или, что, то же самое

Для всех x  x_0, удовлетворяющих условию , где  - меньшее из ₁ и ₂. Это означает, что

.

Теорема доказана.

6. Первый замечательный предел

Теорема 6. Предел функции в точке x = 0 существует и равен 1, то есть: .

Доказательство:

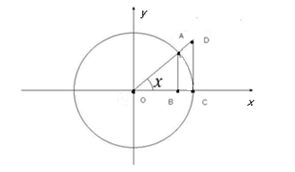
1. Пусть x > 0 (x )

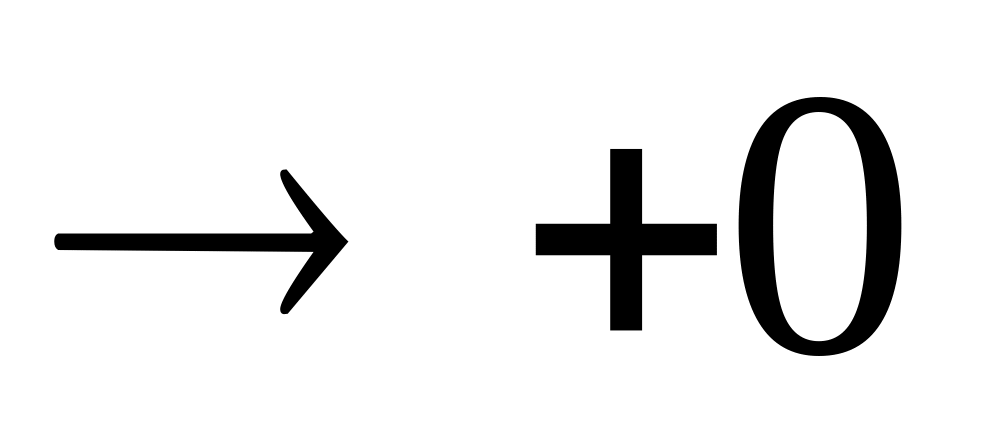(1)

; ;

(x – в радианах)

Подставим в соотношение (1) полученные значения площадей:

,

,

Так как все части двойного неравенства положительные, можно переписать так:

Т.к. то по теореме 5: .

2. Пусть x<0 (x )

(по доказанному в первом случае)

Следовательно, .

Теорема доказана.