6.2 Вопросы теплопередачи

Теплопередача в охлаждающую среду происходит путем теплопро­водности частей машины и теплорассеяния с охлаждаемых поверх­ностей.

Для подавляющего большинст­ва электрических машин в качестве охлаждающей среды используется воздух, который и будет рассматри­ваться в анализе процессов тепло­передачи.

Теплоотдача на границе нагре­той поверхности и охлаждающего воздуха определяется опытным за­коном Ньютона — Рихмана, соглас­но которому рассеиваемый поверх­ностью тепловой поток равен:

(69)

Соответственно перепад темпе­ратуры 6 между поверхностью и воздухом составит:

(70)

где q— плотность теплового пото­ка на охлаждаемой по­верхности;

ά— коэффициент теплоотдачи поверхности.

На пути движения потока Q воз­никают перепады температуры в изоляции обмоток, сердечниках ста­торов (роторов), при переходе тепла с поверхностей к охлаждающему воздуху и др.

Согласно основному закону теп­лопроводности плотность теплового потока в направлении его движения прямо пропорциональна темпера­турному градиенту в этом же на­правлении:

(71)

Коэффициент λ называется ко­эффициентом теплопро­водности или удельной теплопроводностью. Знак минус поставлен потому, что при положительном направлении тепло­вого потока температурный гради­ент является отрицательным, то есть в этом направлении температура по­нижается.

При одномерном течении тепла, например, в направлении оси х имеем:

(72)

Электрическая машина является сложным сочетанием разнородных тел, обладающих неодинаковыми физическими свойствами. Поэтому определение картины теплового по­ля при установившемся режиме и наличии внутренних источников теп­ла потребовало бы решения систе­мы дифференциальных уравнений Пуассона, имеющих для каждого тела в отдельности следующий вид:

(73)

где , , —удельные теплопро­водности по осям x, у, z в рассматривае­мом

элементарном объеме тела;

р — количество тепла, или удельные поте­ри, выделяемые в том же объеме.

При отсутствии источников теп­ла в рассматриваемом объеме и одномерном течении теплового по­тока получим уравнение:

(74)

Откуда в результате решения его найдем :

(75)

где

В этом случае имеет место ли­нейное возрастание температуры.

При передаче тепла в одном на­правлении с постоянным значением величины

р имеем параболическое распределение температуры вдоль оси х:

(76)

постоянные c₁ и с₂ определяют­ся из граничных условий. Например, для стержня обмотки, уло­женного в паз (рисунок 11), уравне­ние распределения температуры вдоль стержня получит вид:

(77)

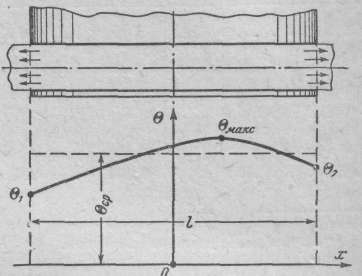
Рисунок 11 - Распределение температуры вдоль стержня обмотки в пазу

При условии на гра­нице с лобовыми частями обмотки средняя температура будет равна:

(78)

а максимальная составит:

(79)

В случае двухмерного движения теплового потока задача становит­ся весьма сложной и решается при­ближенно.

При неустановившемся режиме проблема теплового расчета стано­вится еще более сложной. В первом приближении температура внутри объема отдельных тел, например сердечника, обмоток, прини­мается постоянной и расчет приво­дится к определению температуры двух-трех однородных тел, связан­ных тепловыми проводимостями или тепловыми сопротивлениями. В дальнейшем уточняются внутрен­ние перепады температуры отдель­ных тел.