Центральная предельная теорема (цпт)

В теории вероятностей существует ряд предельных теорем, указывающих условия, при выполнении которых распределение вероятностей нормированных сумм случайных величин сходится к нормальному (гауссовскому) распределению. Рассмотрим одну из них.

Пусть количество успехов в испытаниях Бернулли и - вероятность успеха в одном испытании, тогда по интегральной теореме Муавра-Лапласа для любого c < d имеет место

.

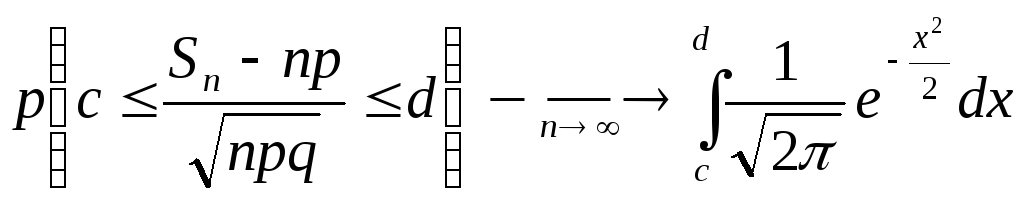Здесь , где .

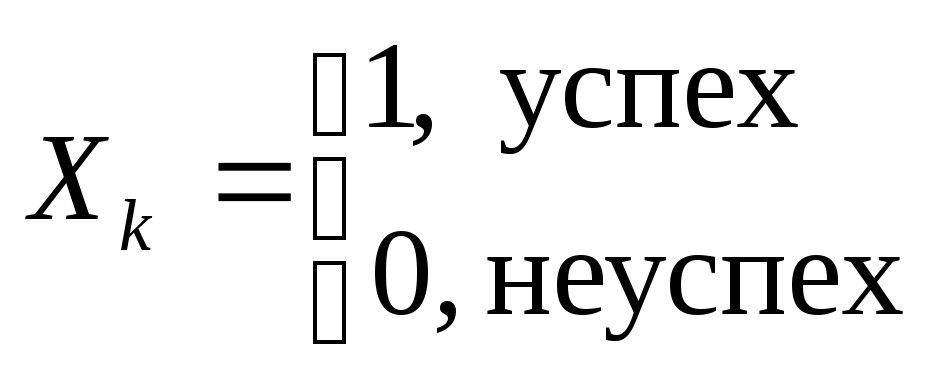Легко видеть, что

,

где , тогда формулировка интегральной теоремы Муавра-Лапласа может быть переписана в новых обозначениях так:

При любых конечных значениях c < d имеет место

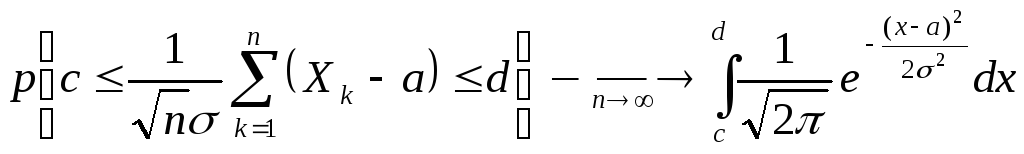(1.26)

Эта теорема носит название «Центральная предельная теорема» .

Здесь последовательность независимых одинаково распределенных (т.е. совпадают функции распределения) случайных величин, a=M(X) - математическое ожидание, дисперсия D(X)= ² <  - имеет конечное значение.

Эту теорему мы сформулировали, используя схему Бернулли, однако отметим, что данная теорема справедлива и в общем случае.

1.2.3. Оценка погрешности математического ожидания исследуемой величины

Пусть для получения оценки математического ожидания a^* случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х), и по ним была найдена выборочная средняя , которая принята в качестве искомой оценки: . Ясно, что если повторить опыт, то будут получены другие возможные значения , следовательно, другая средняя, а значит и другая оценка a^* . При этом возникает вопрос о величине допускаемой ошибки: которую из полученных значений математического ожидания выбрать в качестве измеренной величины? Ограничимся отысканием лишь верхней границы  допускаемой ошибки с заданной вероятностью (надёжностью) : .

Интересующая нас верхняя грань ошибки  есть не что иное, как «точность оценки» математического ожидания по выборочной средней при помощи доверительных интервалов. Рассмотрим три случая оценки ошибки для нормального (гауссовского) распределения плотности вероятности.

1. Случайная величина Х имеет нормальное распределение, и её среднее квадратичное отклонение  известно.

В этом случае с надёжностью  верхняя граница ошибки

, (1.27)

где N число испытаний (разыгранных значений Х); t – значение аргумента функции Лапласа, при котором ,  - известное среднее квадратичное отклонение Х.

2. Случайная величина Х имеет нормальное распределение, причём её среднее квадратичное отклонение  неизвестно.

В этом случае с надёжностью  верхняя граница ошибки

, (1.28))

где N – число испытаний; s – «исправленное» среднее квадратичное отклонение, которая находится из эксперимента, находят по таблице приложения.

3. Случайная величина Х распределена по закону, отличному от нормального распределения.

В этом случае при достаточно большом числе испытаний с надёжностью, приближённо равной , верхняя граница ошибки может быть вычислена по формуле (1.28), если среднее квадратичное отклонение  случайной величины Х известно; если же  неизвестно, то можно подставить в формулу (1.28) его оценку s – «исправленное» среднее квадратичное отклонение. Заметим, что чем больше N, тем меньше различие между результатами, которые дают обе формулы.

4. При использовании одной нормально распределенной случайной величины Х для оценки измеряемой величины используется правило трех «сигм»

(1.29)

Если мы рассматриваем N независимых случайных величин с одной и той же плотностью распределения, то

, (1.30)

где среднее арифметическое от независимых случайных величин.