3.7 Состовление схемы алгоритма расчета приведенного момента движущих сил и расчет в одном конкретном положении.

Приведенный момент сил имеет вид: ;

Определение выполняется из условия равенства мгновенных модностей: ;

Тогда: , где и – проекции силы на оси координат, и – проекции аналога скорости на оси координат,

– передаточная функция i-го звена к кривошипу, = -1, так как направлена по часовой стрелке;

На рисунке 3.7 изображены векторы всех сил, действующих на механизм.

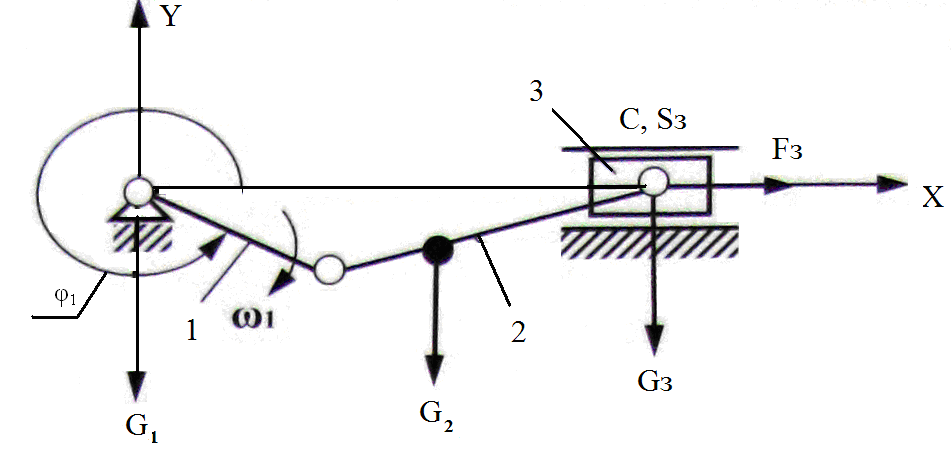
Рисунок 3.7 Направление активных сил

Для данного механизма сила отрицательна.

Рассчитываем приведенный момент движущих сил для положения

№ 3 (, которое является контрольным положением.

, где проекция аналога скорости точки s2 на ось y.

Приведённый момент сил сопротивления определяется из условия, что при установившемся режиме движения изменение кинетической энергии машины за цикл равно нулю, т.е.

откуда за цикл

Работа движущих сил вычисляется по формуле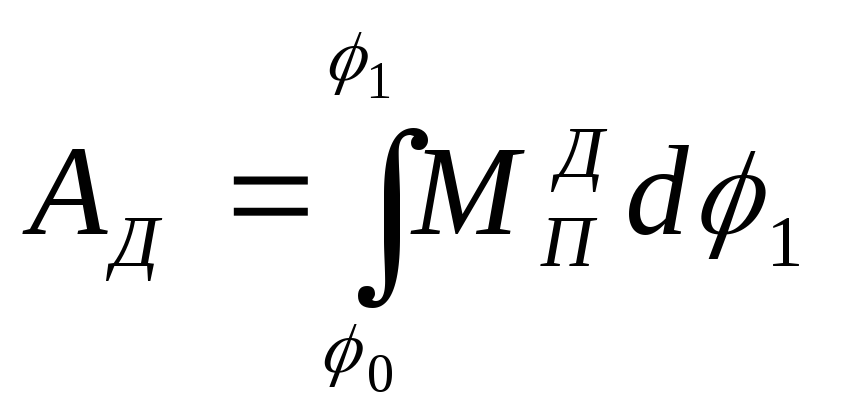

Интегрирование выполняется численным методом по правилу трапеции:

где – шаг интегрирования в радианах.

n – число интервалов деления одного оборота кривошипа.

С учётом при ;

3.8 Состовление схемы алгоритма расчёта переменной составляющей приведенного момента инерции и состовляющих. Расчёт и состовляющих и расчёт контрольных положений

Переменная составляющая определяется из условия равенства кинетических энергий, т.е. кинетическая энергия звена приведения, имеющая момент инерции , равна сумме кинетических энергий звеньев, характеризуемых переменными функциями:

Разделив это выражение на , с учётом того что , получим: .

Для звеньев 2,3 кривошипно-шатунного механизма получим:

;

, где

.

Производная , необходимая в последующем для определения закона движения звена приведения, имеет вид:

В постоянную составляющую приведенного момента инерции входят моменты инерции кривошипа и всех вращающихся звеньев:

; ; ;

3.9 Составление схемы алгоритма по определению постоянной составляющей приведенного момента инерции по методу Мерцалова

В основу расчёта положен метод Н.И. Мерцалова. Для определения изменения кинетической энергии машины предварительно определяем работу сил сопротивления . Для i – ого положения: ,где . Тогда .

Изменение кинетической энергии звеньев с постоянным приведенным моментом инерции равно:

где - кинетическая энергия звеньев, создающих переменную составляющую . По методу Н.И. Мерцалова определяется приближенно по средней угловой скорости :

Далее из полученного цикла значений (рис. 3.8.) находим максимальную и при минимальном величины, используя которые вычисляем максимальный перепад кинетической энергии: .

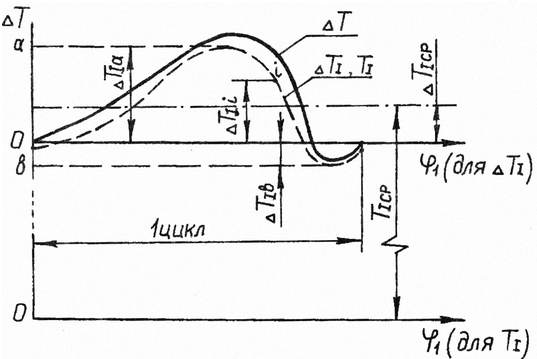
Рисунок 3.8 Массив значений

Тогда необходимая величина , при которой имеет место вращение звена приведения с заданным коэффициентом неравномерности , равна

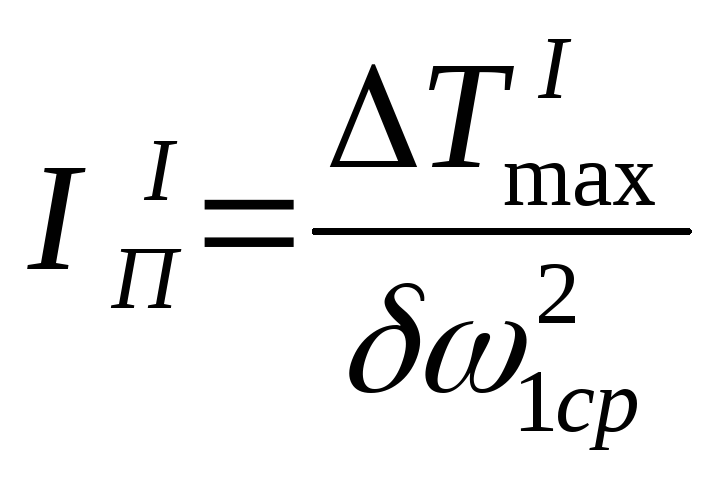, где

Момент инерции маховика определяется по формуле:

где - приведенный момент инерции всех вращающихся масс машины (ротора двигателя, зубчатых колес, кривошипа).

Иногда величина может оказаться больше полученного значения . В этом случае не требуется установки маховика. Тогда реальный коэффициент неравномерности вращения равен:

3.10 Определение закона движения звена приведения

С помощью зависимости , используемой при определении постоянной составляющей приведенного момента инерции по методу Мерцалова, получаем зависимость угловой скорости звена приведения

Из рисунка 3.8 видно, что для любого положения кинетическая энергия звеньев, обладающих постоянным приведенным моментом инерции , равна: , где , .

Так как , значение угловой скорости.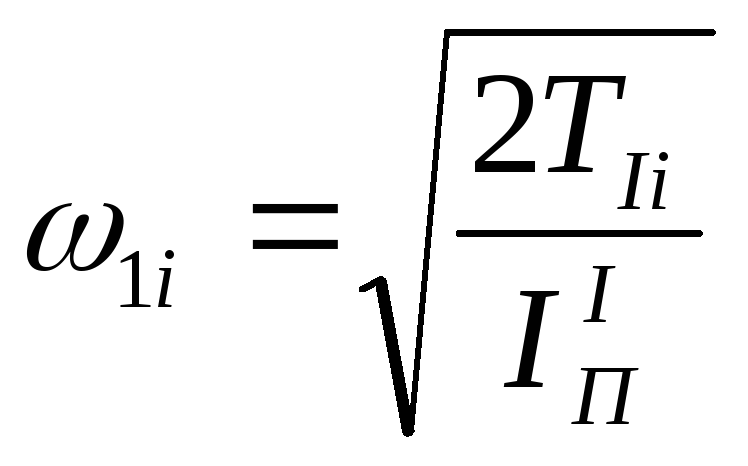

Угловое ускорение определяется из дифференциального уравнения движения звена приведения:.