Угловое ускорение при вращении тела

Угловым ускорением называют степень изменения угловой скорости.

За вектор углового ускорения ε при вращении тела вокруг неподвижной точки принимают вектор, который характеризует изменение угловой скорости ω в данный момент как по числовой величине, так и по направлению. Такой характеристикой является производная по времени от вектора угловой скорости ω. Таким образом, угловое ускорение определяется так:

     

Рис. 3.3

В общем случае угловое ускорение не направлено по мгновенной оси, а, как производная по времени от вектора ω, параллельно касательной к годографу этого вектора. Условимся угловое ускорение ε изображать в любой точке прямой, параллельной этой касательной годографа угловой скорости u, но проходящей через неподвижную точку тела (рисунок 3.3). Прямая, по которой направлен вектор углового ускорения, называется осью углового ускорения и обозначается E.

23) Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 2.11). 

При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M₁M₂ ) совершают одинаковые движения.

                                    

Рисунок 2.11

Рисунок 2.12

    Отрезок M₁M₂  движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.

    На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy  из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A  с последующим поворотом на угол φ  вокруг точки A₁. Это же перемещение можно выполнить иначе. 

    Например, перемещая пластинку поступательно с траекторией точки B , с последующим поворотом вокруг B₁  на угол φ. Траектории точек A  и B различны, а угол поворота в обоих случаях  одинаков. 

     Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде:

                                 x_A=x_A(t),  y_A=y_A(t),  φ=φ(t).

    Точка A  в этом случае называется полюсом. Если принять за полюс точку B , то получим уравнения:

                                x_B=xB(t),  y_B=yB(t),  φ=φ(t)

    За полюс выбирается точка, закон движения которой известен.

24) При любом движении твердого тела проекции скоростей двух точек тела на прямую, соединяющую эти точки, равны.

Доказательство:

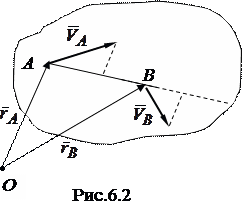Возьмем произвольные точки тела А и В, скорость которых в некоторый момент времени обозначим и . Выберем произвольную неподвижную точку будут вектор-функциями и .

Из рис. 6.2

. (6.3)

Продифференцируем по времени обе части равенства (6.3)

, или

. (6.4)

Так как при движении тела длина отрезка АВ не меняется, т.е. , то из второго свойства производной вектора по скалярному аргументу

.

Проектируя теперь векторное равенство (6.4) на направление вектора , получим

. (6.5)

 

25) Понятие МЦС удобно использовать при определении скоростей точек плоской фигуры.

Скорость любой точки плоской фигуры равна ее линейной скорости при вращении этой фигуры вокруг МЦС (рис. 39).

.

Положение мгновенного центра скоростей можно определить, если известны:

а) угловая скорость плоской фигуры и скорость какой-либо ее точки;

б) направление скорости каких-либо двух ее точек;

в) точка, скорость которой в данный момент равна нулю.

скорости точек плоской фигуры пропорциональны их расстоя­ниям от МЦС.

Полученные результаты приводят к следующим выводам.

1. Для определения мгновенного центра скоростей надо знать то­лько направления скоростей  и  каких-нибудь двух точек А и В плоской фигуры (или траектории этих точек); мгновенный центр скоростей находится в точке пересечения перпендикуляров, вос­ставленных из точек А и В к скоростям этих точек (или к каса­тельным к траекториям).

2. Для определения скорости любой точки плоской фигуры, надо знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В. Тогда, вос­ставив из точек А и В перпендикуляры к  и  , построим мгно­венный центр скоростей Р и по направлению  определим направ­ление поворота фигуры. После этого, зная v_А, найдем скорость v_М любой точки М плоской фигуры. Направлен век­тор  перпендикулярно РМ в сторону поворота фигуры.

3. Угловая скорость  плоской фигуры равна в каждый данный момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от мгновенного центра скоростей Р:

26)

27) Основной закон механики (второй закон Ньютона) был сформулирован Ньютоном в отличие от работ предшествующих ученых в дифференциальной форме. Это позволило рассмотреть многочисленные задачи, где движение определяется переменными силами. Механические задачи, решенные Галилеем, превратились после исследований Ньютона в очень простые частные случаи.  

Основные законы механики Галилея — Ньютона сформулированы для свободной материальной точки, т. е. для точки, на перемещение которой не наложено никаких ограничений и движение которой зависит только от начальных условий и действующих на нее сил. Однако как в природе, так и в искусственных сооружениях и машинах, созданных человеком, мы чаще имеем дело с несвободными материальными телами, перемещения которых в пространстве ограничены другими телами. Любое тело, ограничивающее свободу перемещения данного тела, называется связью, наложенной па это тело например, для лампы, подвешенной на шнуре, связью является шнур для книги, лежащей на столе, связью является стол для двери, подвешенной на петлях, связями являются петли и т. д.  

28)  Две основные задачи динамики.

В динамике решаются две основных задачи:

1)      по заданному движению точки или системы определить силы, производящие это движение.

2)      по заданным силам, действующим на точку или систему, определить движение этих объектов.

Прямая задача динамики: по кинематическому характеру движения материальной точки (вообще материального объекта) определить силу (силы), вызывающую это движение.

Прямая задача: В общем случае задана масса точки m и кинематическое уравнение её движения .

Алгоритм решения: .

Замечаем, что решение прямой задачи динамики предполагает двойное дифференцирование исходного кинематического уравнения движения материальной точки.

Примечание: При решении конкретных задач динамики материальной точки целесообразно кинематическое уравнение её движения записывать не в векторной форме, а в координатной, либо в естественных осях.

29) Дифференциальные уравнения поступательного движения твердого тела:  и т.д. – проекция внешней силы. Все точки тела движутся так же, как и его центр масс С. Для осуществления поступательного движения необходимо, чтобы главный момент всех внешних сил относительно центра масс был равен 0: =0.

Дифференциальные уравнения вращения твердого тела вокруг неподвижной оси: ,

J_z – момент инерции тела относительно оси вращения z, – момент внешних сил относительно оси вращения (вращающий момент). _, e – угловое ускорение, чем больше момент инерции при данном _, тем меньше ускорение, т.е момент инерции при вращательном движении является аналогом массы при поступательном. Зная _, можно найти закон вращения тела j=f(t), и, наоборот, зная j=f(t), можно найти момент. Частные случаи: 1) если = 0, то w = const – тело вращается равномерно; 2) = const, то e = const – вращение равнопеременное. Уравнение аналогичное дифференциальному уравнению прямолинейного движения точки .

30)