36) Кинетическая энергия твердых тел. В конце этого вопроса краткий вариант, постарайся и его пихнуть.

Кинетическая энергия тела равна сумме кинетических энергий всех материальных точек, на которые это тело разбито: . (5.16) Если тело движется поступательно, то скорость каждой его точки _i одинакова и равна скорости движения центра масс, _С. Тогда формула (5.16) для кинетической энергии поступательного движения примет вид: , (5.17) где 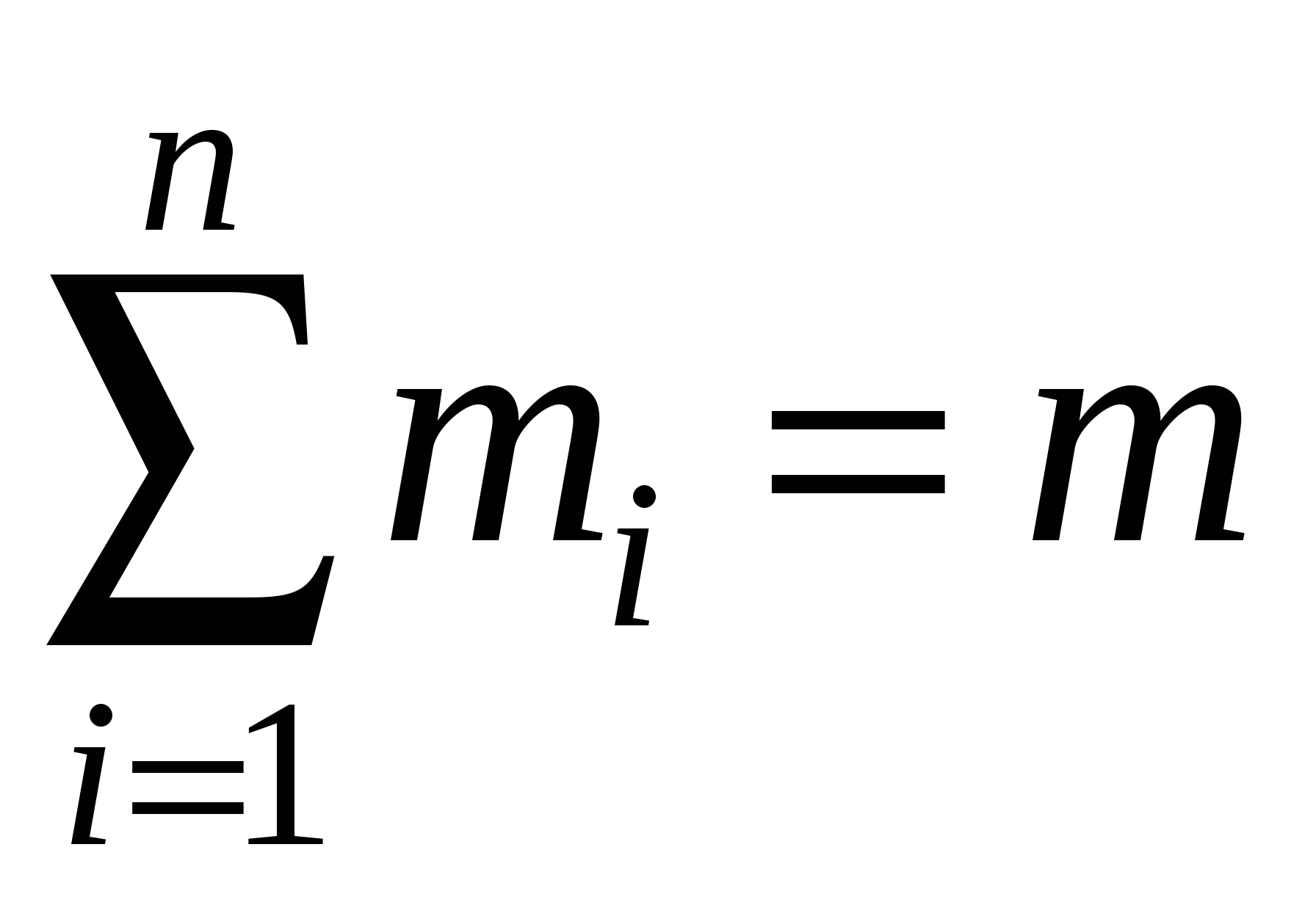- масса тела. Кинетическая энергия твердого тела вращающегося вокруг неподвижной оси Если тело вращается вокруг неподвижной оси с угловой скоростью , то линейная скорость i-ой точки равна _I = r_i , где r_i  расстояние от этой точки до оси вращения. Поэтому, из (4.17) следует: , (5.18) где I_z  момент инерции тела относительно оси вращения. Таким образом, кинетическая энергия твердого тела вращающегося вокруг неподвижной оси, пропорциональна квадрату угловой скорости.

Кинетическая энергия механической системы- скаляр, равный сумме кинетических энергий всех точек системы:.

При поступательном движении:

При вращательном движении:

При плоскопараллельном движении: , где d - расстояние от центра масс до МЦС.

37)Теорема об изменении кинетической энергии точки и системы.

Кинетическая энергия материальной точки- скаляр, равный половине произведение массы точки на квадрат ее скорости.

Основное уравнение динамики: , до множим на элементарное перемещение:;;. Интегрируя полученное выражение:

Теорема: изменение кинетической энергии материальной точки на некотором перемещении равно работе силы, действующей на точку, на том же перемещении.

, так как работа внутренних сил равна нулю, то: .

Теорема: изменение кинетической энергии механической системы на конечном перемещении равно сумме работ внешних сил на том же перемещении.

38)Осевые моменты инерции однородных тел.

Момент инерции- скалярная величина, равная произведению массы на квадрат расстояния.

Планарный момент инерции- момент инерции относительно плоскости:;осевой - относительно оси:;полярный - относительно полюса:; центробежный момент инерции:.

Радиус инерции- расстояние от оси до воображаемой точки, в которой необходимо сосредоточить массу тела, чтоб момент инерции этой точки относительно заданной оси был равен моменту инерции данного тела относительно этой же оси:.

Главные оси и главные моменты инерции.

Главная ось инерции- ось, относительно которой центробежный момент равен нулю. Если для тела существует материальная ось симметрии, то главная ось инерции совпадает с ней. Если все центробежные моменты инерции равны нулю, то каждая из осей является главной осью инерции.

Главная центральная ось инерции- центральная ось инерции, проходящая через центр масс.

Главные моменты инерции- моменты инерции относительно главных осей.

39)Теорема о моменте инерции относительно параллельной оси.

Теорема: Момент инерции относительно оси равен сумме момента инерции относительно параллельной ей центральной оси и произведение массы тела на квадрат расстояния меду осями: I_z= I_zc+ mh².

Для однородного стержня: I_zc= ml²/12;

для однородного кольца: I_zc= mR²;

для однородного диска: I_zc= mR²/2;

Моменты инерции некоторых однородных тел:

стержень массы m и длины L: ; .

Однородный сплошной диск с центром в точке С радиуса R и массы m: . Полый цилиндр: ,

цилиндр с массой распределенной по ободу (обруч): .