15 Трение качения

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.

Рассмотрим круглый цилиндрический каток радиуса R и веса Р, лежащий на горизонтальной шероховатой плоскости. Приложим к оси катка силу Q (рис. 83, а), меньшую Fпр Тогда в точке А возникает сила трения F, численно равная Q, которая будет препятствовать скольжению цилиндра по плоскости. Если считать нормальную реакцию N тоже приложенной в точке А, то она уравновесит силу Р, а силы Q и F образуют пару, вызывающую качение цилиндра. При такой схеме качение должно начаться, как видим, под действием любой, сколь угодно малой силы 0.

Рис. 83

Истинная же картина, как показывает опыт, выглядит иначе.

Объясняется это тем, что фактически вследствие деформаций тел касание их происходит вдоль некоторой площадки АВ (рис. 83, б). При действии силы Q интенсивность давления у края А убывает, а у края В возрастает. В результате реакция N оказывается смещенной в сторону действия силы Q. С увеличением Q это смещение растет до некоторой предельной величины к. Таким образом, в предельном положении на каток будут действовать пара Qпр, F с моментом и уравновешивающая ее пара N, Р с моментом Nk.

Из равенства моментов находим Qпр*R=Nk или

Пока Q<Qпр каток находится в покое; при Q>Qпр  начинается качение.

Входящая в формулу (43) линейная величина k называется коэффициентом трения качения. Измеряют величину k обычно в сантиметрах. Значение коэффициента к зависит от материала тел и определяется опытным путем. Приведем приближенные значения этого коэффициента (в см) для некоторых материалов

Отношение k/R для большинства материалов значительно меньше статического коэффициента трения f0 Этим объясняется то, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса, катки, шариковые подшипники и т. п.).

Задача 34 . Определить, при каких значениях угла а (рис 84) Цилиндр радиуса R, лежащчй на наклонной плоскости, остается в покое, если коэффициент трения качения равен k.

Решение Рассмотрим предельное положение равновесия, когда a-a1. Разлагая силу Р на составляющие P1 и P2 (рис 84), находим, что в этом случае сдвигающая сила Qпр=P1≈P*sin(a1) а нормальная реакция N=P2≈P*cos(a1). Тогда по формуле (43)

При уменьшении k до нуля угол a1 также убывает до нуля. Отсюда заключаем, что равновесие сохранится при любом угле a<a1. Полученным резльтатом можно воспользоваться для экспериментального определения коэффициента k, находя угол а1 из опыта.

Примечание. Цилиндр при а≈a1 в покое, если одновременно коэффициент трения скольжения f0 цилиндра о плоскость будет таков, что f0≥tg(a1) (см задачу 30 в § 25), т. е. если f0>k/R что обычно имеет место Но если окажется, что f0<k/R то при а=а1 цилиндр не будет в покое и начнет скользить вдоль плоскости,

Рис. 84

16) Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учёта их инертности (массы) и действующих на них сил. Под движением мы понимаем в механике изменение с течением времени положения данного тела в пространстве по отношению к другим телам. Для определения положения движущегося тела или точки с тем телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, которая вместе с телом образуют систему отсчёта. Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство. Все измерения в нём производятся на основании методов евклидовой геометрии. Время является скалярной, непрерывно изменяющейся величиной. Отсчёт времени ведётся от некоторого начального момента, о выборе которого в каждом случае уславливаются. Кинематически задать движение или закон движения тела (точки) значит задать положение этого тела относительно данной системы отсчёта в любой момент времени. Установление математических способов задания движения точек или тел является одной из важных задач кинематики. Основная задача кинематики состоит в том, чтобы, зная закон движения данного тела (или точки), определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой из его точек в отдельности.

17)  Векторный способ задания точки.

В этом случае положение точки на плоскости или в пространстве определяется вектором-функцией 

r=r(t)            (1.1)

Рисунок 1.1

     Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки.

Годограф r, т.е. положение концов этого вектора в пространстве, определяет траекторию движущейся точки. Ее скорость в этом случае определяется как производная от радиуса-вектора и направлена по касательной к годографу r (по касательной к траектории движения точки, рисунок 1.1):

V=dr/dt           (1.2)

а

б

Рисунок 1.2

     Ускорение точки (изменение ее скорости) определяется как производная от скорости:

      Вектор ускорения направлен по касательной к годографу вектора скорости  (рисунок 1.2, б).

18) Координатный способ задания точки.

  В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:

x=x(t)

y=y(t)                   (1.4)

z=z(t)

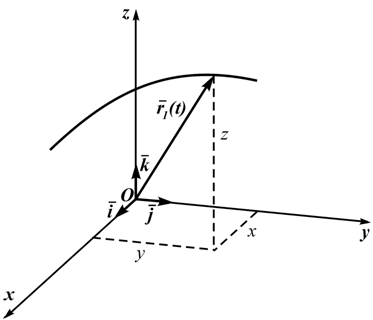
Рисунок 1.3

     Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.

    Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):

       r(t)=i⋅x(t) ⊕ j⋅y(t) ⊕ k⋅z(t) (1.5)

     Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:

    То есть: 

 

     Направление вектора скорости определяется с помощью направляющих косинусов:    

 

     Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.

     Аналогичны формулы для определения ускорения точки:

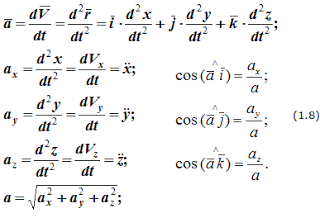
     Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.