19) Естественный способ задания движения точки

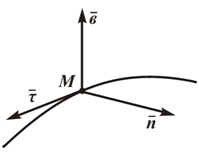
Рисунок 1.4

На рисунке 1.4:

τ-орт касательной;

n-орт нормали;

b-орт бинормали;

     При естественном способе задания движения предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.

     Единичные орты  τ, n ,b определяют направление соответствующих осей в каждой точке кривой.

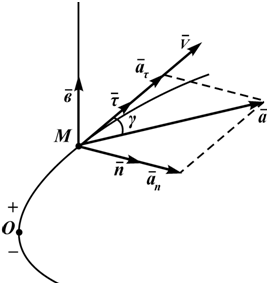
Рисунок 1.5

     Чтобы задать закон движения точки естественным способом необходимо:

1) знать траекторию движения;

2) установить начало отсчета на этой кривой;

3) установить положительное направление движения;

4) дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t) .

   Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).

     

   Скорость точки определяется по формулам (1.9)

                                          V=τ⋅dS/dt,    V=dS/dt.   (1.9)

      Первая формула определяет величину и направление вектора скорости, вторая формула только величину.

     Ускорение определяется как производная от вектора скорости:

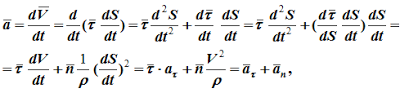
   т.е.  a=a_τ+a_n.    (1.10)

     В формуле (1.10)

     a_τ=τ⋅dV/dt=τ⋅d²S/dt², a_τ=dV/dt=τ⋅d²S/dt²- касательное ускорение; оно характеризует быстроту изменения величины скорости точки;

     a_n=n⋅V²/ρ, a_n=V²/ρ - нормальное ускорение точки; характеризует быстроту изменения направления вектора скорости;

    ρ - радиус кривизны траектории в данной точке (например, для окружности:ρ=R  , для прямой линии ρ=∞ ).

     Полное ускорение точки определяется следующим образом (рисунок 1.5):

     Выше отмечалось,  что всегда можно перейти от одного способа задания закона движения точки к другому. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.

    Например,  

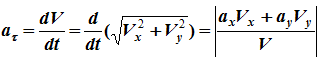
или   a_τ=acosγ (рисунок 1.5).       

    Далее 

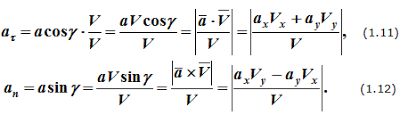
20) Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.

Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д. 

Рис. 1.1

Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.

Доказательство. 

Если выбрать две точки твердого тела А  и В  (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением

Траектория точки А  – это кривая, которая задается функцией r_A(t), а  траектория точки B – это кривая, которая задается функцией r_B(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.

Продифференцируем по времени выражение

Получаем

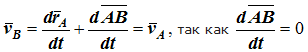
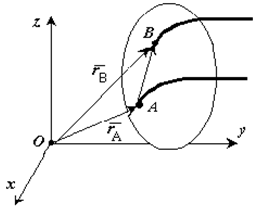
Рис. 1.2

Продифференцируем по времени скорость и получим выражение a_B = a_A. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

21) Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П , одна из которых неподвижна, а другая жестко связана с телом.

 φ=φ(t) – уравнение вращательного движения твердого тела.

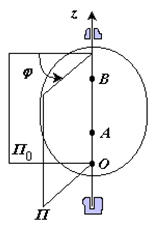
Рис. 1.3

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту.  За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин).  Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

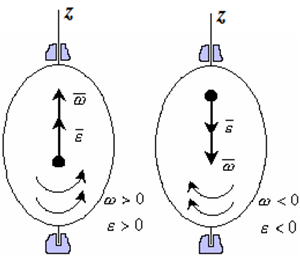
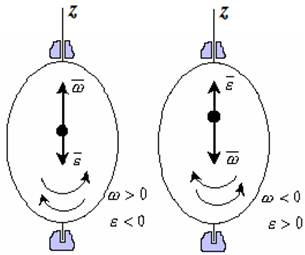
Рис. 1.4

Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону.  Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.

При ε <0 и ω <0 – тело вращается ускоренно  в отрицательную сторону.  Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz .

Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторы ω и ε направлены в противоположные стороны.

Если ε >0 при ω <0, то имеем замедленное вращение в отрицательную сторону. Векторы ω и ε направлены в противоположные стороны.

Если угловая скорость  ω=const, то вращательное движение называется равномерным. Уравнение равномерного вращения

φ=φ₀+ωt

Если угловое ускорение ε=const, то вращательное движение называется равнопеременным. 

Уравнение равнопеременного вращения

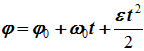
и уравнение, выражающее угловую скорость в любой момент времени

 ω=ω₀+εt

представляют совокупность основных формул вращательного равнопеременного движения тела.

22) Угловой скоростью называют векторную величину, характеризующую быстроту вращения твердого тела, определяемую как приращение угла поворота тела за промежуток времени.

Рассмотрим бесконечно малый промежуток времени Δt → 0, за который твердое тело совершает поворот на бесконечно малый угол Δα вокруг мгновенной оси Ω (рисунок 3.2). 

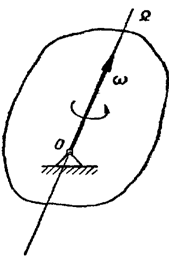
Рис. 3.2 

Предел, к которому стремится отношение  Δα / Δt, называется угловой скоростью твердого тела в рассматриваемый момент времени

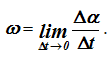
Угловая скорость является векторной величиной. Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки.