10) Пара сил. Момент пары. Эквивалентность пар

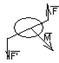
 Пара сил – система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело. Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется величиной – момент пары. Он определяется:

Его модулем = F*d. d – расстояние между линиями действия сил пары, называется плечом пары. Положением в пространстве плоскости действия пары. Направлением поворота пары в этой плоскости.

Момент пары сил – вектор m(или M), модуль которого равен произведению модуля одной из сил пары, на ее плечо, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.

Две пары, лежащие в || плоскостях и имеющие одинаковый момент эквивалентны.

Все пары в пересекающихся плоскостях можно заменить одной парой с моментом, равным сумме моментов этих пар. Для абсолютно твердого тела пара – свободный вектор, определяемы только моментом. Момент перпендикулярен плоскости образуемой парой.

Пару можно заменить параллельной ей равной силе и парой с моментом, равным произведению этой силы на расстояние до новой точки приложения.

Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой парой механическое состояние тела не изменяется, т. е. не изменяется движение тела или не нару­шается его равновесие.

Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно перено­сить в плоскости ее действия в любое положение.

Рассмотрим еще одно свойство пары сил, которое является основой для сложения пар.

Не нарушая состояния тела, мож­но как угодно изменять модули сил и плечо пары, только бы момент па­ры оставался неизменным.

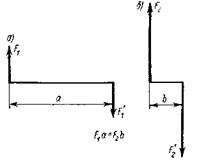
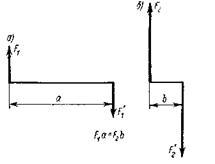
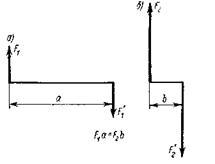Заменим пару сил сплечом a  новой парой плечом b так, чтобы момент пары оставался тем же. Момент заданной пары сил М₁ = F₁a. Момент новой пары сил М₂ = F₂b. По определению пары сил эквивалентны, т. е. производят одинаковое действие, если их моменты равны.

Если изменив значения сил и плечо новой пары, мы сохраним равенство их моментов М_г= М_г или F₁a = F₂b, то состояние тела от такой замены не нарушится.

Итак, вместо заданной пары с плечом а мы получили эквивалентную парус плечом b.

11. Теорема о параллельном переносе силы

Равнодействующая системы сходящихся сил непосредственно находится с помощью закона параллелограмма сил. Очевидно, что аналогичную задачу можно будет решить и для произвольной системы сил, если найти для них метод, позволяющий перенести все силы в одну точку. Такой метод дает следующая теорема: силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, Куда сила переносится.

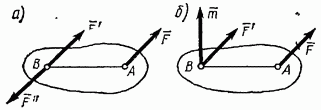
Рис. 37

Пусть на твердое тело действует сила F, приложенная в точке А (рис. 37, а). Действие этой силы не изменяется, если в любой точке В тела приложить две уравновешенные силы F'такие, что F''. Полученная система трех сил и представляет собой силу F, равную F, но приложенную в точке В, и пару F, F с моментом

Последнее равенство следует из формулы (15). Таким образом, теорема доказана. Результат, даваемый теоремой, можно еще изобразить так, как это показано на рис. 37, б (силу F на этом рисунке надо считать отброшенной). Рассмотрим примеры, иллюстрирующие теорему.

Пример 1. Чтобы удержать в равновесии однородный брус АВ длиной 2а и весом Р, надо приложить в его середине С направленную вверх силу Q, по модулю равную Р (рис. 38, а). Согласно доказанной теореме силу Q можно заменить силой Q', приложенной к концу А бруса, и парой с моментом, модуль которого m=Q*a.

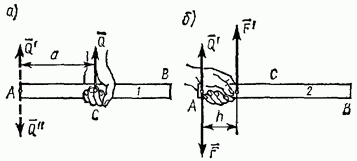
Рис. 38

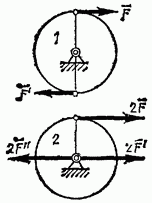
Рис. 39

Если плечо этой пары уменьшить до величины h (рис. 38, б), то образующие ее силы F, F' надо увеличить так, чтобы было F*h=Q*a. Следовательно, чтобы удержать брус за его конец А, надо кроме силы Q приложить еще пару F, F. Этот результат, вытекающий из доказанной теоремы, непосредственно «ощущает» рука человека, удерживающая брус за его середину (рис. 38, а) или за конец (рис. 38, б).

Пример 2. На барабан 1 радиуса r намотаны в противоположных направлениях две нити, к концам которых прикладывают силы F и F' = -F (рис. 39); на барабан 2 того же радиуса намотана одна нить, к которой прикладывают силу, равную 2F Рассмотрим, чем будут отличаться действия этих сил.

На барабан 1 действует только пара сил F, F' с моментом, численно равным 2Fr  вращающая барабан. Силу, действующую на барабан 2, можно заменить силой 2F'=2F приложенной к оси барабана, и парой 2F, 2F'' В результате находим, что на этот барабан действуют: 1) пара с численно таким же, как и в первом случае, моментом 2Fr вращающая барабан, и 2) сила 2F' оказывающая давление на ось барабана.

Итак, оба барабана будут вращаться одинаково. Но при этом ось второго барабана испытывает давление, равное 2F а ось первого барабана никакого давления не испытывает.