12. Центр параллельных сил

Понятие о центре параллельных сил используется при решении некоторых задач механики, в частности при определении положений центров тяжести тел.

Рассмотрим сначала две параллельные силы и R=0 и M0=0 приложенные к телу в точках A1 И А2 (рис. 103). Очевидно, что Эта плоская система сил имеет равнодействующую R=F1+F2 линия действия которой параллельна слагаемым силам и проходит через некоторую точку С, лежащую на прямой A1A2.  Положение точки С найдем с помощью теоремы Вариньона. Согласно этой теореме Mc(R)=Mc(F1)+Mc(F2) или 0=F1*h1-F2*h2=F1*A1C*cos(a)- F2*A2C*cos(a), откуда

В равенство (54) входят модули F1 и F2 рассматриваемых сил. Поэтому, если силы F1 и F2 повернуть около точек A1 и A2 в одну и ту же сторону на один и тот же угол, то образуются две новые параллельные силы F'1 и F'2 имеющие те же модули F1 и F2 следовательно, для сил F'1 и F'2  равенство (54) сохранится и линия действия их равнодействующей R' тоже пройдет черезточку С. Такая точка называется центром параллельных сил F'1 и F'2 

Теперь рассмотрим систему параллельных и одинаково направленных сил  приложенных к твердому телу в точках  (рис. 104).

Эта система сил имеет равнодействующую модуль которой

Если каждую из сил системы поворачивать около точки ее приложения в одну и ту же сторону на один и тот же угол, то будут получаться новые системы одинаково направленных параллельных сил с теми же модулями и точками приложения (см. например, показанные пунктиром силы на рис. 104). Равнодействующая каждой из таких систем сил будет иметь тот же модуль R, но всякий раз другое направление.

Рис.

Рис. 104

Покажем, что при всех таких поворотах линия действия равнодействующей проходит через одну и ту же точку С. В самом деле, сложив сначала силы F1 и F2 найдем по формуле (54), что их равнодействующая R1 (на рис. 104 не показана) будет всегда проходить через точку с1 положение которой определяется равенством Сложив затем силы и R1 и F3 найдем, что их равнодействующая, являющаяся одновременно равнодействующей сил F1,F2,F3 всегда проходит через аналогично определяемую точку с2 лежащую на прямой с1A3 и т. д. Доведя этот процесс последовательного сложения сил до конца, убедимся, что равнодействующая R всех сил действительно проходит всегда через одну и ту же точку С, положение которой по отношению к точкам A1,A2….An  т. е. к телу, будет неизменным.

Точка С, через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол, называется центром параллельных сил.

Найдем координаты центра параллельных сил. Положение точки С по отношению к телу является неизменным и от выбора системы координат зависеть не будет. Возьмем поэтому произвольные координатные оси Охуz и обозначим в этих осях координаты точек: A1(x1 y1 z1), А2(х2 у2 z2)…. C(xc yc zc)

Пользуясь тем, что от направления сил положение точки С не зависит, повернем сначала силы около их точек приложения так, чтобы они стали параллельны оси Oz и применим к повернутым силам F'1,F'2 …. F'n теорему Вариньона. Так как R является равнодействующей этих сил, то по формуле (46), беря моменты относительно оси Oy найдем, что

Но из чертежа [или из равенств (47)] видно, что My(R')=Rxc так как R'=R аналогично My (F'1)=F1x1так как F'=F и т. д. Подставляя все эти величины в равенство (56), получим

Отсюда определим Xc

Для координаты Yc аналогичную формулу найдем, беря моменты относительно оси Ox. Чтобы определить Zc повернем опять все силы, сделав их параллельными оси Oy и применим к этим силам (изображенным пунктиром с точками) теорему Вариньона, беря моменты относительно оси Ox Это даст:

откуда определим Zc

Окончательно получим следующие формулы для координат центра параллельных сил:

где R определяется равенством (55).

Заметим, что формулы (55) и (57) будут справедливы и для параллельных сил, направленных в разные стороны, если считать Fh величинами алгебраическими (для одного направления со знаком плюс, а для другого — минус) и если при этом R не равно 0.

Центр тяжести твердого тела.

Область, в каждой точке которой на помещенную туда материальную частицу действует сила, зависящая от положения (координат) этой точки, называется силовым полем. Примером силового поля является поле тяготения (поле сил притяжения к Земле или к любому другому небесному телу).

На каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, которую называют силой тяжести (вопрос о том, что собой представляет сила тяжести, будет рассмотрен в § 92).

Эти силы образуют поле сил тяжести.

Для тел, размеры которых очень малы по сравнению с земным радиусом, силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела. Поле тяжести, в котором выполняются, эти два условия, называют однородным полем тяжести.

Равнодействующую сил тяжести p1,p2…. pn  действующих на частицы данного тела, обозначим Р (рис. 105). Модуль этой силы называется весом тела и определяется равенством

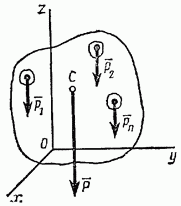
Рис. 105

При любом повороте тела силы pk остаются приложенными в одних и тех же точках тела и параллельными друг другу, изменяется только их направление по отношению к телу. Следовательно, по доказанному в § 31, равнодействующая Р сил pk будет при любых положениях тела проходить через одну и ту же неизменно связанную с телом точку С, являющуюся центром параллельных сил тяжести pk. Эта точка и называется центром тяжести тела. Таким образом, центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве. Что такая точка существует, следует из доказанного в § 31.

Координаты центра тяжести, как центра параллельных сил, определяются формулами (57), следовательно,

где xk, yk, zk — координаты точек приложения сил тяжести  pk действующих на частицы тела.

Отметим в заключение, что согласно определению центр тяжести — это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).